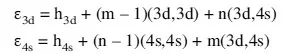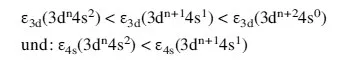Koordinationschemie

Lutz H. Gade

• Verlag: Wiley-VCH
• Jahr: 2012
• ISBN drucken: 9783527295036
• eBook-ISBN: 9783527663941
• Auflage: 1
• Thema: Physical Sciences
• Thema: Inorganic Chemistry

Seit Alfred Werner seine Koordinationslehre vor etwas mehr als hundert Jahren formulierte, hat sich die Komplexchemie der Übergangsmetalle rasant zu einem der wichtigsten Forschungsgebiete der Anorganischen Chemie entwickelt. Wie facettenreich die Koordinationschemie sein kann, deutet sich schon an der Variabilität der Verbindungen an, zu denen so kleine Molekale wie Hexacarbonylchrom ebenso wie Metallenzyme geharen.

Dieses Lehrbuch richtet sich an Studenten im Hauptstudium. Alle wichtigen Aspekte der Koordinationschemie - beispielsweise die Ligandenfeldtheorie, die Bindungstheorie, die Eigenschaften, Reaktivitat und Strukturen der Komplexe, die Reaktionsmechanismen und die spektroskopischen Untersuchungsmethoden - sind enthalten.

Verschaffen Sie sich einen Einblick in dieses faszinierende Gebiet von den Anfangen bis hin zu den modernsten Entwicklungen.

IV

Das Zentralmetallatom

In diesem Teil werden die Grundlagen für das Verständnis der faszinierenden physikalischen und chemischen Eigenschaften der Übergangsmetallkomplexe vorgestellt und diskutiert. Dabei werden wir zunächst von der elektronischen Struktur der einzelnen Metallatome ausgehen und daraus dann ein theoretisches Modell für die Komplexe entwickeln. Alfred Werner faßte Komplexe als aus mehreren für sich existenten Segmenten (Zentralatom + Liganden) aufgebaute Moleküle auf. Analog wird bei der theoretischen Beschreibung der physikalischen Eigenschaften von Koordinationsverbindungen verfahren, bei der das Zentralmetallatom im Blickpunkt steht und die Liganden ein mehr oder weniger starkes „Störfeld" darstellen. Die Stärken und Schwächen dieser Vorstellung werden im Mittelpunkt der folgenden Kapitel stehen. Die wesentlichen Lernziele sind dabei:

1) Die Beschreibung der elektronischen Eigenschaften der Übergangsmetallatome auf der Grundlage von Slaters Atomtheorie (Kap. 13).

2) Das Verständnis der Konzepte der Ligandenfeldtheorie, ihrer Formulierung auf der Grundlage gruppentheoretischer Prinzipien und der Grenzen ihrer Anwendbarkeit (Kap. 14).

3) Die lokale Formulierung des Ligandenfeld-Konzepts im Rahmen des „Angu- lar-Overlap-Modells" bei der Beschreibung von Komplexen mit niedriger Symmetrie (Kap. 15).

4) Die Beschreibung der Bindungsverhältnisse in Komplexen mit Hilfe der Molekülorbitaltheorie und die Interpretation der Ligandenfeldparameter ausgehend davon (Kap. 16).

Auf der Grundlage der in den Kapiteln 14–16 diskutierten theoretischen Modelle werden wir uns in Teil V mit den charakteristischen physikalischen Eigenschaften von Koordinationsverbindungen der Übergangsmetalle beschäftigen.

13 Die elektronische Struktur der Übergangsmetallatome und -ionen

13.1 Die Elektronenkonfigurationen der Übergangsmetalle

Den Aufbau des Periodensystems kann man mit Hilfe des Orbital-Konzepts und des Pauli-Prinzips verstehen, wobei die Orbitale die Einelektronenwel- lenfunktionen sind, mit denen man die Wellenfunktionen für die Elektronen in Atomen (und Molekülen) konstruiert (Abschnitt 13.4). Ausgangspunkt für die Orbitalbeschreibung ist das atomare „Kepler-Problem“ des Wasserstoffatoms, das man geschlossen lösen kann. Eine geschlossene Lösung ist für Mehrelektronenatome nicht mehr möglich, weshalb man das komplizierte Vielteilchen-Problem mit dem Verfahren der effektiven Wechselwirkungen zu lösen versucht. Dabei ersetzt man die Zweiteilchen-Wechselwirkungen (Elektron-Kern-Anziehung, Elektron-Elektron-Abstoßung) zwischen den einzelnen Teilchen durch ein globales Feld, das zwar nicht von vornherein bekannt ist, aber zum Beispiel iterativ bestimmt werden kann. Hängt dieses globale Potential nur vom Kernabstand ab, so spricht man von der Zentralfeld-Näherung, auf die wir im Zusammenhang mit der Atomtheorie von Slater in Abschnitt 13.4 noch zurückkommen werden. Die bei der Lösung der Schrödinger-Gleichung des Mehrelektronensystems in der Zentralfeld-Nöherung erhaltenen Orbitale ähneln denen des Wasserstoffatoms.

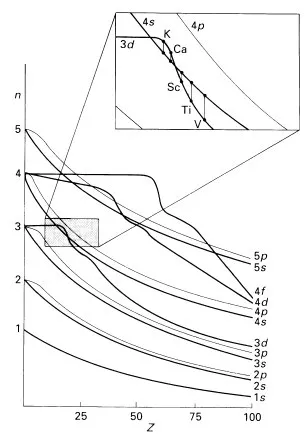
Eine Folge der Coulomb-Wechselwirkung der Elektronen untereinander, die näherungsweise durch die Wechselwirkung jedes Elektrons mit einem globalen Feld ausgedrückt werden kann, ist die Aufhebung der Entartung der Energien der Orbitale mit gleicher Hauptquantenzahl. Im Bild dieser Näherung verursacht dies die unterschiedliche räumliche Aufenthaltswahrscheinlichkeit von Elektronen der Orbitale verschiedener Drehimpulsquantenzahl (unterschiedlichen „Durchdringung“ des Atomrumpfs) und die dadurch bedingten Unterschiede in der Abschirmung der Kernladung. Wie sich die Atomorbitalenergien in Abhängigkeit von der Kernladungszahl verändern, ist in Abbildung 13.1 schematisch dargestellt.

Wie man in Abbildung 3.1 sieht, verändert sich die relative Energie der Orbitale in Abhängigkeit von Z. So liegt beispielsweise das 3d-Orbital im Wasserstoffatom energetisch niedriger als das 4s-Orbital, dies ändert sich jedoch bereits im Bereich von Z = 7 (Stickstoff). Zwischen Z = 7 und 20 liegt das 4s-Orbital hingegen energetisch unter dem 3d-Orbital, eine Folge der besseren Durchdringung des Atomrumpfs durch das 4s-Orbital (Abb. 13.2).

Obwohl die 3d-Orbitalenergie ab Z =20 unter der der 4s-Orbitale liegt, sind die Konfigurationen der elektronischen Grundzustände der 3d-Metalle mit wenigen Ausnahmen (s. u.) 3dⁿ4s². Weshalb befinden sich die Valenzelektronen im Grundzustand also nicht alle in den energetisch tiefer liegenden 3d- Orbitalen, haben die 3d-Metalle also nicht die Grundzustandskonfiguration 3dⁿ⁺²? Eine Erklärung mit Hilfe des Orbitalbildes ist dann möglich, wenn wir als Orbitalenergien den Mittelwert der verschiedenen Terme, die zu einer Konfiguration gehören, bilden (Konfigurations-Mittelwerte) und die einzelnen Multiplettzustände zunächst einmal nicht berücksichtigen.²

Abb. 13.1. Atomorbitalenergien von neutralen Mehrelektronenatomen als Funktion der Ordnungszahl (Kernladungszahl). Der vergrößerte Ausschnitt zeigt die energetische Reihenfolge im Bereich von Z = 20 (Ca), in dem die Reihe der 3d-Übergangsme- talle beginnt. Aufgrund der größer werdenden Anziehung der Elektronen durch die Kernladung mit steigender Kernladungszahl fallen die Orbitalenergien ab. Der Abfall ist für die „inneren“ Orbitale am stärksten, da die Abschirmung des Kerns für diese Elektronen am schwächsten ist.

Abb. 13.2. Aufenthaltswahrscheinlichkeitsdichte für ein Elektron in Abhängigkeit vom Kernabstand in einem 3d- und 4s-Orbital von Scan- dium.¹ Obwohl die inneren Maxima des 4s-Orbitals die Durchdringung des Atomrumpfs bewirken, befindet sich beim Scandium – wie auch bei den übrigen 3d-Metallen – das Maximum des 3d-Orbitals näher am Kern als das äußere Maximum des 4s- Orbitals. Daher erfährt das 3d-Orbital die Erhöhung der Kernladung um jeweils eine Einheit fast ohne Abschirmung beim Gang von Kalium (Z =19) über Ca (Z = 20) zu Scandium (Z =21).

Im Falle von Scandium (3d¹4s²) ist die Orbitalenergie ε_3d gleich der Energie eines Elektrons, das sich im Feld der Ladung des Atomrumpfs und der beiden 4s-Elektronen befindet. Sie unterscheidet sich daher sicherlich von ε_3d der Konfigurationen 3d²4s¹ und 3d³. Ebenso hängt ε_4s von der Grundzustands- konfiguration ab, was verdeutlicht, daß die Darstellung in Abbildung 13.1 für die Erklärung der Grundzustandskonfigurationen der Übergangsmetalle zu oberflächlich ist.

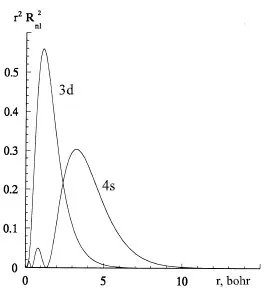
Die Konfigurationen der Grundzustände werden dann verständlich, wenn man sich vergegenwärtigt, daß das 4s-Orbital viel raumerfüllender und folglich diffuser als die 3d-Orbitale ist (Abb. 13.2). Zwei Elektronen in 3d-Orbita- len stoßen sich also stärker ab als zwei 4s-Elektronen, so daß für die Elektron-Elektron-Wechselwirkung die folgende Hierarchie gilt: (4s,4s) < (3d,4s) < (3d,3d).³ Aus der Abhängigkeit der Orbitalenergien von der Elektronenkonfiguration 3d^m4sⁿ:

– wobei h die effektive Einelektronenenergie eines 3d- oder 4s-Elektrons, die kinetische Energie und Elektron-Kern-Anziehung, im globalen Feld des Atomrumpfs ist – folgt für die Orbitalenergien:

Dies bedeutet, daß sowohl ε_3d als auch ε_4s mit zunehmender Besetzung der 3d-Orbitale ansteigen (Abb. 13.3).

Da das 4s-Orbital das höchste besetzte Orbital in den Übergangsmetallionen von Sc bis Zn ist, sollte man erwarten, daß eine Ionisation bevorzugt aus diesem Orbital stattfindet. Dies ist die korrekte Schlußfolgerung auf der Basis einer falschen Argumentation.⁴ Der Grund für die dⁿ-Konfiguration aller Übergangsmetallionen ist...

Inhaltsverzeichnis

• Cover
• Series Page
• Title Page
• Copyright
• Dedication
• Foreword
• Preface
• I: Einführung
• II: Strukturen
• III: Symmetrie
• IV: Das Zentralmetallatom
• V: Physikalische Eigenschaften von Komplexen und deren Untersuchung
• VI: Die Liganden
• VII: Reaktionen von Koordinationsverbindungen
• VIII: Metall-Metall-Bindungen in Komplexen
• Anhang
• Register