Verschränkte Systeme

Die Quantenphysik auf neuen Wegen

Jürgen Audretsch

• Verlag: Wiley-VCH
• Jahr: 2012
• ISBN drucken: 9783527404520
• eBook-ISBN: 9783527660568
• Auflage: 1
• Thema: Naturwissenschaften
• Thema: Physik

Dieses einführende Lehrbuch für Studenten höherer Semester der Physik, Chemie und Informatik behandelt ein in jüngster Zeit dynamisch expandierendes Gebiet der Physik.
Das Buch befasst sich u.a. mit den Themen Quanteninformationstheorie, Quantenkommunikation, Quantencomputing, Teleportation, verborgene Parameter, Welcher-Weg-Markierung, Quantenmessprozess, POVM, Quantenkanäle und vermittelt dadurch nicht nur ein vertieftes Verständnis der Quantentheorie, sondern auch ein Basiswissen, um die schnelle Entwicklung des Gebiets zu verfolgen, bzw. in ein Spezialgebiet der Forschung einsteigen zu können.
Kommentierte Empfehlungen für weiterführende Literatur sowie Übungsaufgaben helfen dem Leser, rasch einen fundierten Zugang zu den theoretischen Grundlagen zukünftiger Schlüsseltechnologien zu finden.
Das Buch kann zur Grundlage von Vorlesungen und Seminaren gemacht werden. Da die benötigten Grundkenntnisse in Mathematik und Quantentheorie in einleitenden Kapiteln dargestellt werden, eignet sich das Buch auch zum Selbststudium.

1

Der mathematische Rahmen

Es ist die Aufgabe der Quantentheorie – genau wie die jeder anderen physikalischen Theorie – das Ergebnis von Experimenten vorherzusagen und diese Prognose zu begründen. Dazu muss man den Zustand des physikalischen Systems zu Beginn eines Experiments beschreiben, man muss die Entwicklung des Systems während des Experiments formulieren und das Ergebnis einer Wechselwirkung mit dem Messapparat vorhersagen können. Der mathematische Rahmen, der sich für die Formulierung der Quantentheorie bewährt hat, ist die Theorie des Hilbert-Raums und die Wahrscheinlichkeitstheorie. Die fundamentale Verknüpfung zwischen mathematischen Größen und physikalischer Realität wird dabei über die folgenden Zuordnungen etabliert:

Quantensystem	↔	Hilbert-Raum
Quantenzustand	↔	Vektor im oder Operator auf dem Hilbert-Raum
Entwicklung des Quantenzustands	↔	Lineare Operatoren, die auf den Vektoren wirken bzw. lineare Operatoren, die auf den Raum der Operatoren (Liouville-Raum) wirken.
Prognosen	↔	Wahrscheinlichkeitstheoretische Aussagen.

Wir werden dieses Grundschema der Quantentheorie noch im Einzelnen darstellen. In diesem Kapitel sollen zunächst die benötigten Definitionen und Sätze zusammengestellt werden. Dabei werden wir nicht alle mathematischen Sätze beweisen. Insbesondere werden wir voraussetzen, dass der Leser schon einmal Kontakt mit der Quantentheorie hatte, sodass die Darstellung knapp gehalten werden kann.

Da wir durchweg d-Niveau-Quantensysteme (d = 2 , 3 , . . .) untersuchen werden, wollen wir eine stark vereinfachende Einschränkung machen:

Mathematische Generalvoraussetzug: Wir betrachten Quantensysteme, die mit Hilfe eines endlich-dimensionalen Hilbert-Raums

der Dimension d = 2, 3, . . . beschrieben werden können.

Die Einschränkung ist gerechtfertigt, weil die wesentlichen begrifflichen Probleme sowie die neuen Konzepte und zentralen Methoden bereits mit Bezug auf einen endlichdimensionalem Hilbert-Raum eingeführt werden können. Wir wollen den konzeptionellen physikalischen Problemen nicht noch mathematische Subtilitäten hinzufügen. Für die meisten physikalisch relevanten Fällen, die eine Beschreibung im unendlich-dimensionalen Hilbert-Raum erfordern, lassen sich die Ergebnisse für endlich-dimensionale Räume direkt übertragen.

Wie in der theoretischen Physik üblich, werden wir die Dirac-Schreibweise benutzen. In diesem Rahmen ist es günstig, die dyadische Zerlegung von Operatoren in den Mittelpunkt der Behandlung zu stellen. Sie ist für praktische Anwendungen wichtig, da sie ein einfaches direktes Ablesen von Operatoreigenschaften und Operatorwirkungen erlaubt.

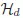
1.1 Hilbert-Raum der Vektoren

1.1.1 Skalarprodukt, Dirac-Schreibweise

Ein d-dimensionaler Hilbert-Raum

, wie er in der Quantentheorie verwendet wird, ist ein linearer Vektorraum über dem Körper der komplexen Zahlen

, auf dem ein Skalarprodukt definiert ist. Die Vektoren bezeichnen wir durch | φ 〉, | ψ 〉, | u 〉, |Φ) usw., |Null 〉 ist der Nullvektor.

Addition, Multiplikation mit einer komplexen Zahl, lineare Unabhängigkeit, Basis und Dimension des Hilbert-Raums

sind analog zu den Begriffen in reellen Vektorräumen definiert.

Je zwei Vektoren | φ 〉 und | ψ 〉 ist als Skalarprodukt(scalar product) oder inneres Produkt (inner product) eine komplexe Zahl zugeordnet, die wir in der Form 〈 φ| ψ 〉 schreiben. Als Grundlage für diese Dirac-Schreibweise¹ (Dirac notation) haben wir einen Ket-Raum mit den Ket-Vektoren | φ 〉, | ψ 〉 ,….. und den hierzu dualen Vektorraum der Bra-Vektoren 〈 χ|, 〈 θ|,….eingeführt (Raum der linearen Funktionale). Es ist eine Korrespondenz zwischen den Vektoren des Ket...

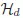
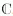
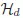
Inhaltsverzeichnis

• Cover
• Title
• copyright
• Vorwort
• 1: Der mathematische Rahmen
• 2: Grundkonzepte der Quantentheorie
• 3: Die einfachsten Quantensysteme: Qubits
• 4: Gemischter Zustand und Dichteoperator
• 5: Shannon-Entropie und klassische Information
• 6: Von-Neumann-Entropie und Quanteninformation
• 7: Zusammengesetzte Systeme
• 8: Verschränkung
• 9: Korrelationen und nicht-lokale Messungen
• 10: Es gibt keine (lokal-realistische) Alternative zur Quantentheorie
• 11: Verschränkung als Hilfsmittel
• 12: Quantencomputer
• 13: Verallgemeinerte Messungen, POVM
• 14: Allgemeine Entwicklung eines offenen Quantensystems und spezielle Quantenkanäle
• 15: Dekohärenz und Ansätze für die Beschreibung des Quantenmessprozesses
• 16: Zwei Realisierungen von Quantenoperationen
• Literatur
• Register