Relative Dauerfestigkeit

Ermittlung der Dauerfestigkeiten im ppm-Bereich

Josef Köhler

• Verlag: De Gruyter Oldenbourg
• Jahr: 2014
• eBook-ISBN: 9783110377934
• Auflage: 1
• Thema: Technik & Maschinenbau
• Thema: Mechanik

Der Dauerbruch metallischer Bauteile wird als mathematische Funktion mit den Variablen Wahrscheinlichkeit, Belastung und Belastungsdauer behandelt. Damit kann man sowohl technische Dauerfestigkeiten für 1 ppm als auch asymptotische Dauerfestigkeiten mit der Wahrscheinlichkeit Null berechnen. Eine einzige Funktion liefert Prognosen für einstufige, mehrstufige und zufällige Belastungen, sowie für alle Einflüsse und für alle Bauteilgrößen.

1 Einleitung

An der TU Berlin haben die Doktoranden Dorff, Mäiß, Dengel und Maennig, an der TU München Bertele, Köhler und Böhm in großer Zahl gleichartige Proben geprüft und die Ergebnisse in Wöhlerdiagrammen ausgewertet. Es resultierten sehr große Streubereiche, die nicht aus Unzulänglichkeiten des Versuches, sondern aus dem Werkstoff kommen. Da man Streuung mit den Werkzeugen der Statistik berechnet, ist es naheliegend, die Wahrscheinlichkeit als dritte Variable neben der Ausschlagsspannung und der Lastspielzahl einzuführen. Weitere Einflussgrößen sind die Mittelspannung, die Bauteilgröße, die Temperatur und die Umgebung.

Mit den Rasterelektronenmikroskopen, die seit 1970 zur Verfügung standen, konnten die Bruchflächen gebrochener Proben und Bauteile analysiert werden. Am mechanisch technischen Labor der TU München wurden in einer Versuchsreihe 250 Bruchflächen analysiert, um die Ereignisse nachzuempfinden, die zum Bruch führten. Daraus resultiert schließlich ein besseres Verständnis der Vorgänge und auch der notwendigen Auswertemethoden.

Üblicherweise ermittelte man im Dauerschwingversuch mit einer geringen Zahl von Proben eine mittlere Wöhlerlinie. Manchmal geben die Prüfer auch 10 % und 90 % Linien an, um die Breite des Streubereiches abzustecken. Für Produzenten von Massenartikeln z.B. in der Automobilindustrie ist dieses Vorgehen unzulänglich. Wenn ein Unternehmen pro Jahr 50 Millionen Bauteile herstellt und vertreibt, benötigt man Aussagen im Bereich von 1 ppm.

In modernen Massenproduktionen versucht man mit der Nullfehlerstrategie die Ausfallwahrscheinlichkeiten einzelner Komponenten möglichst bei 1 ppm (parts per million) zu halten, um die gewünschte Zuverlässigkeit der Gesamtsysteme zu gewährleisten. Bei geometrischen Fehlern kann man die notwendigen Nachweise durch Messungen erbringen. Selbst das gelingt nur mit automatisierten Messmethoden. Wenn man nämlich sicherheitsrelevante Bauteile zu 100 % vermessen muss, dann muss alle 0,5 Sekunden ein Bauteil fertig vermessen und dokumentiert werden. Derartige Systeme existieren und funktionieren heute bereits.

In der Zuverlässigkeitsanalyse wären diese Nachweise nur mit vielen Probanden in langen Testreihen möglich. Ein Dauerschwingversuch auf einem elektromagnetischen Resonanzpulsator oder einem servohydraulischen Pulsator benötigt zwei Tage für zehn Millionen Lastwechsel. Es erscheint unmöglich, für jeden Werkstoff eine Million Bauteile zu prüfen, um Ergebnisse in ppm zu erzielen. Man ist deshalb auf Prognosen angewiesen. Gesucht ist die zuverlässige Ermittlung der Dauerfestigkeit mit ca. 0 % bzw. 1 ppm Bruchwahrscheinlichkeit. Im Folgenden wird ein einfaches und praxiserprobtes Verfahren vorgestellt, eben diese Dauerfestigkeit zu definieren. Die Wöhlerlinie mit der Bruchwahrscheinlichkeit ca. Null nennt der Autor „Nullbruchlinie“ [1], ihren Schnittpunkt mit einer Grenzlastspielzahl „Nullbruchwert“. Das Verfahren erlaubt es, mit einer geringen Probenzahl die Nullbruchlinie statistisch gesichert zu bestimmen. Darüber hinaus wird gezeigt, wie man mit einigen Laborversuchen eine Basis zur Vorhersage der Dauerfestigkeit bei unterschiedlichen Betriebszuständen schafft.

2 Begriffe, Bezeichnungen

σA	Ausschlagsspannung
σm	Mittelspannung
σa	Ausschlagsspannung der Dauerfestigkeit
σa0,∞	Ausschlagsspannung mit Bruchwahrscheinlichkeit 0, Bruchlastspielzahl ∞
σaE,∞	Erwartungswert der Ausschlagsspannung bei der Bruchlastspielzahl ∞
σaE,0	Erwartungswert der Ausschlagsspannung bei der Bruchlastspielzahl 0
σa0,0	Ausschlagsspannung mit Bruchwahrscheinlichkeit 0, Bruchlastspielzahl 0
σa0.63,D	Charakteristischer Wert der Ausschlagsspannung bei der Grenzlastspielzahl
σa0.000001,D	Nullbruchwert bei 1ppm, Grenzlastspielzahl D
σa0.63,0	Charakteristischer Wert der Ausschlagsspannung, Bruchlastspielzahl 0
σa0.63,∞	Charakteristischer Wert der Ausschlagsspannung, Bruchlastspielzahl ∞
σa0.000001,∞	Nullbruchwert mit Bruchwahrscheinlichkeit 1ppm, Bruchlastspielzahl ∞
σaHmax	maximale Spannung einer Kerbe nach Hooke’schem Gesetz
Rm	Zugfestigkeit
R	Lastverhältnis σU / σO
N	Bruchlastspielzahl
ND	Grenzlastspielzahl
Nc	mittlere Bruchlastspielzahl
z	Exponent der Wöhlerlinie
G(σa)	Verteilung der Dauerfestigkeit
u1–α	Normiertes Merkmal der Normalverteilung
b	Steilheit der Weibullverteilung
α	Irrtumswahrscheinlichkeit
V, V0	Prüfvolumen
r	Krümmungsradius einer Kerbe
a	Risslänge (halbe Probenbreite)
L	Prüflänge
d	Probendicke
t	Kerbtiefe
M	Rissgeometrie
s	Standardabweichung der Stichprobe
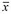	Mittelwert der Stichprobe
g	Wahrscheinlichkeitsdichte
G	Verteilungsfunktion
n	Stichprobenumfang
r	Merkmal
x	Extremes Merkmal
x0	Inkubationswert (Grenzwert des Definitionsbereiches)
αn	charakteristisches Merkmal
μ	Mittelwert der Grundgesamtheit
σ	Standardabweichung der Grundgesamtheit
Γ	Gammafunktion
B	Bestand
A	Ausfallmenge
λ	Ausfallrate
L	Losgröße
F	Funktionswahrscheinlichkeit

Die Kernstücke dieses Buches sind die Kapitel „Auswertungen“ und „Streubandfunktion.“ Einführende Kapitel zur Versuchstechnik, Belastung, Fraktografie, Statistik, Bruchmechanik, Bruchwahrscheinlichkeit, Extremwerttheorie, Bruchmechanik und statistischer Größeneinfluss sind zum Einlesen voran gestellt. Diese Kapitel sind allerdings nur soweit ausgeführt, wie sie zum Verständnis der Kernaussagen nötig sind.

Das Wöhlerdiagramm wird üblicherweise als zweidimensionale Darstellung der Ausschlagsspannung in Abhängigkeit der Bruchlastspielzahl verwendet. In der DIN 50100 (1978) versucht man aus dieser zweidimensionalen Variablen eine eindimensionale Größe zu gewinnen, indem die Bruchlastspielzahl als Grenzlastspielzahl konstant gesetzt wird.

In der DIN 50100 gibt es deshalb nur eine einzige Dauerfestigkeit. Dieses Vorgehen ist für Ingenieure typisch aber nicht zielführend. Zu einem ganzheitlichen System kommt man erst, wenn man die Dauerfestigkeit als dreidimensionale Variable Ausschlagsspannung in Abhängigkeit der Bruchlastspielzahl und Bruchwahrscheinlichkeit behand...

Inhaltsverzeichnis

• Relative Dauerfestigkeit
• Weitere empfehlenswerte Titel
• Titel
• Über den Autor
• Impressum
• Vorwort
• Inhaltsverzeichnis
• 1 Einleitung
• 2 Begriffe, Bezeichnungen
• 3 Belastung
• 4 Bruchkinetik, Fraktografie
• 5 Bruchmechanik
• 6 Bruchwahrscheinlichkeit
• 7 Extremwerttheorie
• 8 Elemente der Auswertung
• 9 Statistischer Größeneinfluss
• 10 Mikrostützwirkung und Makrostützwirkung
• 11 Versuchstechnik
• 12 Auswertungen
• 13 Streubandfunktion
• 14 Erweiterungen undAnpassung der Konstanten
• 15 Anhang
• 16 Beispiele
• Literatur
• Stichwortverzeichnis