David Lewis und seine mereologische Interpretation der Zermelo-Fraenkelschen Mengenlehre

Eine Rekonstruktion

Philipp Werner

• Verlag: De Gruyter
• Jahr: 2015
• eBook-ISBN:
  9781614519362
• Thema: Mathematics
• Thema: Applied Mathematics

In seinem wichtigen Buch "Parts of Classes" hat David Lewis eine Reduktion von ZFC auf eine Mereologie zweiter Stufe skizziert. Sein Resultat nimmt in vorliegender Rekonstruktion folgende Form an: ZFC ist in M (der klassischen Mereologie zweiter Stufe) plus "Es gibt eine stark unerreichbare Partition" parametrisiert interpretierbar. In den Beweis geht ein, dass geordnete Paare in M plus "Es gibt eine unendliche Partition" parametrisiert interpretierbar sind. Die Arbeit beleuchtet den logischen und philosophie-geschichtlichen Hintergrund von "Parts of Classes", gibt eine Einführung in die Mereologie zweiter Stufe und schließt mit einem recht einfachen Beweis für "ZFC ist (die Konsistenz von ZFC vorausgesetzt) in einer konsistenten Mereologie zweiter Stufe parametrisiert interpretierbar".

1 Einleitung

1.1 Hintergrund der Arbeit

1.1.1 Nominalismus, Mengen und Fusionen

Gemäß einer genauso gängigen wie vagen Charakterisierung besteht der oder eine Variante des Nominalismus in der Ablehnung abstrakter Gegenstände.

Mengen sind das Paradebeispiel abstrakter Gegenstände. Jede Katze ist konkret, die Menge der Katzen ist etwas abstraktes – und als solche für den Nominalisten nicht akzeptabel. Zudem kann der Nominalist mit Verweis auf Russell ein logisches Argument gegen den Mengenbegriff anführen: intuitiv sollte es zu jeder Eigenschaft F die Menge der F geben. Die übliche erststufige Formalisierung dieses Postulats ist inkonsistent.1

Der Fusionsbegriff ist dem Nominalist sympathischer, denn die Fusion konkreter Gegenstände ist konkret: die Fusion der Katzen ist der aus allen Katzen bestehende Gegenstand. Er ist zwar unzusammenhängend über die Welt verstreut, aber dennoch konkret. Der Fusionsbegriff wird auch nicht vom logischen Argument getroffen. Zu jeder nicht-leeren Eigenschaft F soll es die Fusion der F geben. Die übliche erststufige Formalisierung dieses Postulats ist konsistent.2

Die vage Frage, ob sich der Mengenbegriff sich durch den Fusionsbegriff ersetzen lässt, besitzt also nicht nur logisches, sondern auch philosophisches Interesse.

Eine erste Analyse lässt daran zweifeln, dass die Frage zu bejahen ist. Zwar teilt der Fusionsbegriff mit dem Mengenbegriff das Merkmal der Rechtseindeutigkeit: sind Eigenschaften umfangsgleich, so sind ihre Fusionen identisch. Aber der Fusionsbegriff ist im Gegensatz zum Mengenbegriff nicht linkseindeutig: Hase und Hasenteil sind nicht umfangsgleich, ihre Fusionen jedoch identisch.3

1.1.2 Elementschaft und Überlappung

Im Hinblick auf eine Präzisierung der gestellten Frage ist es günstig, den Blick auf Theorien der Elementschaftsbeziehung ε und Theorien der Überlappungsbeziehung ∘ zu lenken. Denn

wird gemeinhin durch

erklärt.4 Welche Axiome sind mit ε bzw ∘ verbunden?

(i) Überlappung ist reflexiv und symmetrisch. Ferner enthalten überlappende Gegenstände einen gemeinsamen Teil. Zusammengenommen führt dies zum so genannten Überlappungsaxiom5

(ii) Das Extensionalitätsaxiom bzw Individuierungsaxiom6

ist äquivalent mit der Forderung der Rechtseindeutigkeit des Mengen- bzw Fusionsbegriffs.

(iii) Die oben angeführten Existenzpostulate gehen über in das Komprehensionsschema

∃z∀u(u ε z ↔ Fu)

bzw das Fusionsschema

Das Komprehensionsschema ist inkonsistent: es enthält die Russell-Antinomie

An konsistenten Instanzen enthält es den mit dem Leeremengeaxiom ∃z∀u¬u ε z äquivalenten Satz

∃z∀u(u ε z ↔ u ≠ u)

sowie das Adjunktmengeaxiom

∀xy∃z∀u(u ε z ↔ uε x ∨ u = y)

Das Fusionsschema ist konsistent. Sowohl das Summenaxiom

∀xy∃z∀u(u ∘ z ↔ x ∘ y ∨ u ∘ y)

als auch das Negataxiom

∀x(∃y¬x ∘ y →∀x∃z∀y(∀u(u ∘ y → u ∘ z) ↔ ¬x ∘ y))

ist mit einer Instanz des Fusionsschemas äquivalent.

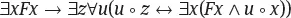
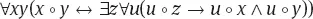
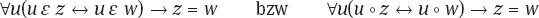
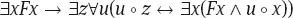
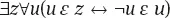
1.1.3 Die Theorien ASE und CI

Die Theorie ASE, eine Teiltheorie der Zermelo-Fraenkelschen Mengenlehre mit Auswahlaxiom ZFC, ist durch Extensionalität...

Inhaltsverzeichnis

• Cover
• Titel
• Impressum
• Inhalt
• Vorwort
• 1 Einleitung
• Teil I: Überlappung
• Teil II: Unendlichkeit und Codierung
• Teil III: Starke Unerreichbarkeit und Elementschaft
• Appendix
• Literatur
• Symbolverzeichnis
• Personenverzeichnis
• Stichwortverzeichnis
• Fußnoten