Brückenkurs Mathematik

Fit für Mathematik im Studium

Jan Peter Gehrke

• Verlag: De Gruyter Oldenbourg
• Jahr: 2016
• ISBN drucken:
  9783110463316
• eBook-ISBN:
  9783110463491
• Thema: Betriebswirtschaft
• Thema: Wirtschaftsmathematik

Ein Brückenkurs muss einiges leisten können: Er wiederholt kompakt den Stoff der Mittel- und Oberstufe, da Studienanfänger hier regelmäßig kleinere oder größere Lücken und Unsicherheiten haben, und er greift auf den relevanten weiterführenden Mathematikstoff der Vorlesungen in angemessenem Maße vor. In der Konsequenz hilft er dabei, Studienanfängern den Schock zu ersparen, der viele beim Anwenden der Mathematik als unverzichtbares Werkzeug in einem wirtschafts- oder naturwissenschaftlichen Studium ereilt. Dadurch wird der große Schritt von der Schule ins Studium ein wenig kleiner.

Genau hier setzt dieses Buch an: Es bereitet mit klarem Blick auf das im Studium Notwendige vor, wiederholt und vermittelt aber auch Neues, das (ohne den Leser zu überfordern) auch in einem Brückenkurs gelehrt werden kann. Zahlreiche Beispiele dienen dazu, den Stoff zu veranschaulichen. Durch eine Vielzahl von Übungen im zusätzlich erhältlichen Übungsbuch kann das Gelernte zudem weiter gefestigt werden. Farbig unterlegte Boxen heben das Wichtigste hervor und helfen, die wesentlichen Inhalte zu erfassen.

Für die vorliegende Auflage wurden alle Grafiken überarbeitet und ein neues Kapitel mit einer kleinen Einführung in die Komplexen Zahlen hinzugefügt.

VIIEinführung in die Differentialrechnung

Im vorliegenden Kapitel beschäftigen wir uns mit einem der Hauptthemen der Mathematik in der Schule und zu Beginn eines entsprechenden Studiums: Einer ausführlichen Behandlung der Differentialrechnung. Von Newton und Leibniz entwickelt, ist sie aus den Naturwissenschaften und der Mathematik nicht mehr wegzudenken. Wir wollen uns hier Schritt für Schritt an dieses interessante Gebiet heranwagen und versuchen, gewisse Fertigkeiten zu entwickeln und zu schulen, welche wichtige Grundlagen für ein Fortschreiten in der mathematischen Welt darstellen.

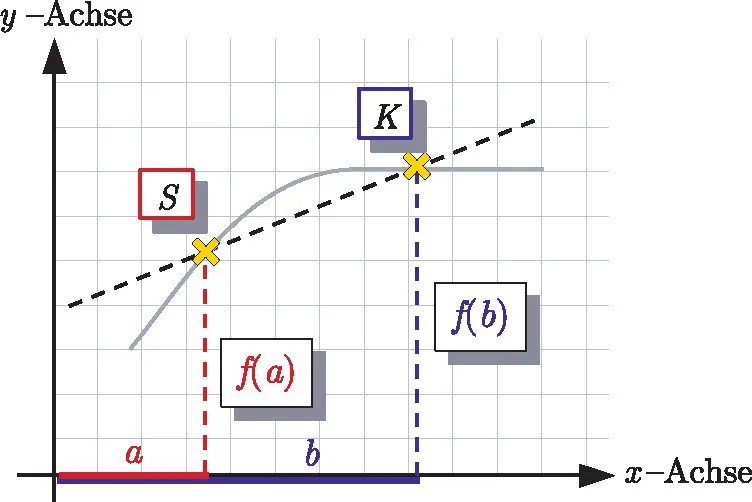
VII.1Vom Differenzen- zum Differentialquotienten

Möchten wir die Steigung einer Funktion in einem Intervall [a; b] ermitteln, so verwenden wir die Formel für die Steigung, die schon bei den linearen Funktionen zum Einsatz kam.

Die (durchschnittliche) Änderungsrate

Im Intervall [a; b] hat eine Funktion, beschrieben durch ihren Funktionsterm f(x), die Steigung

Diese Steigung nennen wir die (durchschnittliche) Änderungsrate der Funktion f im Intervall [a; b] oder einfach nur den Differenzenquotienten.

Wenn wir uns das in einem Beispiel anschauen (Abbildung VII.1.1), erkennen wir, dass der Graph der Funktion f von der Geraden, die durch die Punkte K(b/f(b)) und S(a/f(a)) geht, in mindestens zwei Punkten, den eben genannten, geschnitten wird. Möchten wir eine genauere Steigung bzw. Änderungsrate haben, so müssen wir das Intervall kleiner wählen. Dieses Vorgehen können wir auf die Spitze treiben, indem wir den einen der beiden Punkte immer näher an den anderen heransetzen. Diesen Vorgang nennen wir dann Grenzübergang. Sofern der Grenzwert existiert, bezeichnen wir ihn als die Ableitung der Funktion f an der gewählten Stelle x0 des festgehaltenen Punktes. Allgemein lässt sich so die Ableitung einer Funktion berechnen.

Abbildung VII.1.1: Skizze zur durchschnittlichen Änderungsrate einer Funktion f auf dem Intervall [a; b].

Anmerkung

Eine Gerade, die den Graphen einer Funktion schneidet, nennen wir Sekante, eine die ihn in einem Punkt berührt Tangente an das Schaubild der Funktion in diesem Punkt.

Zum Merken – Der Weg zum Differentialquotienten

Wir legen einen Punkt K (x0/ f(x0)) fest. Anschließend setzen wir den zweiten Punkt immer näher an diesen heran. Wir schreiben: x → x0. Wir können den Differenzenquotienten nun auf zwei Arten bilden, um ihn dann mittels eines Grenzübergangs zum Differentialquotienten umzuwandeln und somit die Ableitung der Funktion zu erhalten.

•Die x-Methode

Wir bilden den Differenzenquotienten auf folgende Weise:

Dann machen wir den Grenzübergang und schreiben deswegen:

Existiert der Grenzwert (muss nicht immer so sein), dann erhalten wir den Differentialquotienten/die Ableitung f′(x0) (lies: f Strich von x0).

•Die h-Methode

Wir bilden den Differenzenquotienten auf folgende Weise:

Dabei ist h ∈ R. Nun machen wir den Grenzübergang:

Existiert der Grenzwert, so haben wir wieder die Ableitung von f an der Stelle x0 erhalten:

Beispiele – Beide Methoden im Ver...

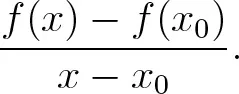
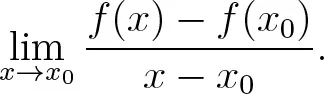
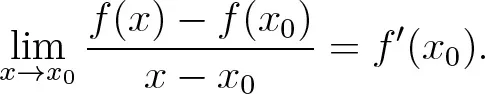
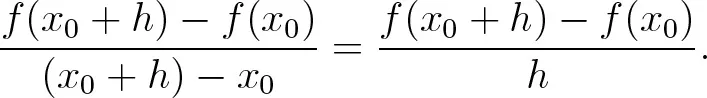
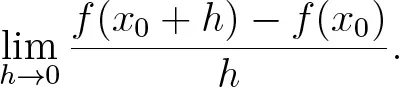
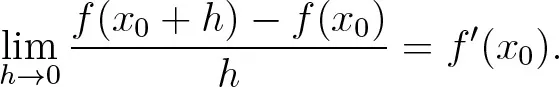
Inhaltsverzeichnis

• Cover
• Titelseite
• Impressum
• Widmung
• Inhaltsverzeichnis
• Vorworte
• I Einführung
• II Lineare Funktionen
• III Quadratische Funktionen
• IV Grundlagen Potenzfunktionen
• V Ganzrationale Funktionen – Eine Einführung
• VI Die vollständige Induktion und (ihre) Folgen
• VII Einführung in die Differentialrechnung
• VIII Über das Lösen linearer Gleichungssysteme
• IX Mit Brüchen muss man umgehen können – Gebrochenrationale Funktionen
• XI Wachsen ist schön – Exponentialfunktionen
• XII Die Ableitung der Umkehrfunktion
• XIV Beweise mit Vektoren führen
• XV Rechnen im Raum – Analytische Geometrie
• XVI Wenn’s nicht direkt geht – Ein wenig Numerik
• XVII Wem’s reell nicht genug ist – Komplexe Zahlen
• Anhang
• Weiterführende Literatur
• Stichwortverzeichnis
• Fußnoten