Übungen zum Brückenkurs Mathematik

Jan Peter Gehrke

• Verlag: De Gruyter Oldenbourg
• Jahr: 2016
• eBook-ISBN:
  9783110463507
• Thema: Betriebswirtschaft
• Thema: Wirtschaftsmathematik

In diesem Übungsbuch finden Sie Aufgaben zum Lehrbuch "Brückenkurs Mathematik – Fit für Mathematik im Studium" samt Ergebnissen und Lösungen zur Vertiefung der dort behandelten Themen. Es werden Ihnen gangbare Lösungswege aufgezeigt, falls Sie beim Rechnen in eine Sackgasse geraten. Haben Sie allerdings einen anderen Weg gefunden als den hier vorgeschlagenen, dann freuen Sie sich, denn dann haben Sie den Kern der Mathematik erfasst: Das eigenständige Lösen von Problemen.

Das Buch kann Ihnen bei der Vertiefung der Themen und der Lösung der vorgestellten Aufgaben behilflich sein. Es kann Ihnen zur Überprüfung Ihrer Rechenschritte und Ergebnisse dienen, es kann Ihnen Hilfestellung sein, wenn Sie doch einmal im finsteren Tal der Mathematik wandern und den Weg nicht finden, und es kann Ihnen Ideengeber sein, wenn Sie so gar nicht wissen, was der Aufgabensteller von Ihnen wissen will. Wichtig ist dabei nur, dass Sie sich um eine eigenständige Lösung der Aufgaben bemühen.

In der Neuauflage finden sich nun auch einführende Aufgaben zum Thema "Komplexe Zahlen". Außerdem wurden alle Grafiken überarbeitet und an die neue farbige Darstellung des Buches angepasst.

FZu Kapitel VII: Einführung in die Differentialrechnung

F.1Aufgaben zu Kapitel VII.1

Aufgabe 1:

Berechnen Sie f′(x0) mit Hilfe der x-Methode für das angegebene x0.

(a)f(x) = 2x2 und x0 = 1.

(b)f(x) = x3 − x und x0 = −1.

(c)

(d)f(x) = x4 + x3 − 1 und x0 = 4. (e) f(x) = x5 und x0 = 1.

(f)

(g)

Aufgabe 2:

Berechnen Sie f′(x0) mit Hilfe der h-Methode für das angegebene x0.

(a)f(x) = x3 und x0 = 1.

(b)f(x) = x4 − x und x0 = 1.

(c)

(d)f(x) = x5 und x0 = 1. (e) f(x) = 2x4 − x und x0 = 3.

(f)

(g)

Aufgabe 3:

Bestimmen Sie die Ableitungsfunktionen der Funktionen mit den Funktionsgleichungen f1(x) = x, f2(x) = x2, f3(x) = x3 und f4(x) = x4. Welche Ableitung hat die Funktion fn mit fn(x) = xn mit n ∈ ℕ ? Stellen Sie eine Vermutung aufgrund der eben gebildeten Ableitungsfunktionen auf.

Aufgabe 4:

Berechnen Sie die Ableitungsfunktion für f mit f(x) = xn (Potenzfunktion). Diese Aufgabe dient als Vorbereitung für das nächste Unterkapitel.

Aufgabe 5:

Weisen Sie mit Hilfe der h-Methode nach, dass die Funktion f mit

f(x) = m · g(x) + c

die Ableitungsfunktion mit der Funktionsgleichung

f′(x) = m · g′(x)

besitzt, wenn die Funktion g differenzierbar, also ableitbar, ist.

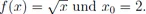
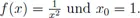
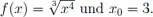
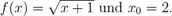
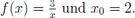
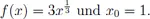
F.2Aufgaben zu Kapitel VII.3.5

Aufgabe 1:

Leiten sie eine Formel für die Ableitung des Produktes dreier Funktionen u, v und w her. Verwenden Sie dazu die „normale“ Produktregel.

Aufgabe 2:

Bestimmen Sie die Ableitungsfunktionen der Funktionen mit den gegebenen Funktionsgleichungen mit Hilfe der gelernten Regeln.

(a)

(b)b(x) = (4x2 − 3x)3

(c)

(d)

(e)

(f)

Aufgabe 3:

Gegeben sei die Funktion f, welche der...

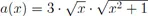
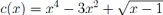
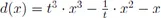
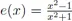
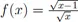
Inhaltsverzeichnis

• Cover
• Titelseite
• Impressum
• Widmung
• Inhaltsverzeichnis
• Vorwort
• A Zu Kapitel II: Lineare Funktionen
• B Zu Kapitel III: Quadratische Funktionen
• C Zu Kapitel IV: Grundlagen Potenzfunktionen
• D Zu Kapitel V: Ganzrationale Funktionen - Eine Einführung
• E Zu Kapitel VI: Die vollständige Induktion und (ihre) Folgen
• F Zu Kapitel VII: Einführung in die Differentialrechnung
• G Zu Kapitel VIII: Über das Lösen linearer Gleichungssysteme
• H Zu Kapitel IX: Gebrochenrationale Funktionen
• I Zu Kapitel X: Trigonometrische Funktionen
• J Zu Kapitel XI: Exponentialfunktionen
• K Zu Kapitel XII: Die Ableitung der Umkehrfunktion
• L Zu Kapitel XIII: Integralrechnung
• M Zu Kapitel XIV: Beweise mit Vektoren führen
• N Zu Kapitel XV: Analytische Geometrie
• O Zu Kapitel XVI: Ein wenig Numerik
• P Zu Kapitel XVII: Komplexe Zahlen
• Q Zu Anhang A: Die Strahlensätze