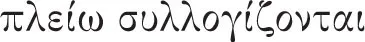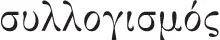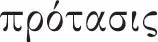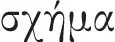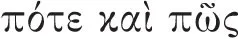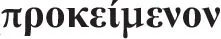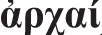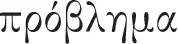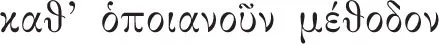Analytica Priora Buch II

,

• Verlag: De Gruyter
• Jahr: 2015
• ISBN:
  9783110431940
• Auflage: 1
• Thema: Philosophie
• Thema: Antike & klassische Philosophie

Der zweite Buch der Ersten Analytiken des Aristoteles ist ein bisher vergleichweise wenig beachteter und wenig kommentierter Text, der immer im Schatten des ersten Buchs mit seiner überragenden Bedeutung für die Geschichte der Logik gestanden hat. Dieser Band der Deutschen Aristoteles-Ausgabe enthält neben einer neuen Übersetzung einen ausführlichen Kommentar, der zum ersten Mal den Text Zeile für Zeile entschlüsselt und so die Fülle von Themen erschliesst, die dort behandelt sind. Die Einleitung gibt einen Überblick über den disparaten und nicht leichten überschaubaren Text, weist seine Bedeutung für die formallogische Rekonstruktion der aristotelischen Syllogistik nach. Schwerpunkte der Interpretation liegen auf dem verwickelten und systematisch besonders spannenden Verhältnis der assertorischen Syllogistik zu modernen nicht-klassischen Logiken (insbesondere im Hinblick auf das Prinzip des ex falso quodlibet), auf die Problematik des Folgerungsbegriffs und auf der Möglichkeit einer nicht-extensionalen Rekonstruktion der Syllogistik. Der Band beitet, den Themen des Textes folgend, ausführliche Informationen zum Verhältnis der Syllogistik in Buch II zur Modallogik, Relevanzlogik, parakonsistenten Logik und konnexiven Logik, zur Theorie des indirekten Beweises bei Aristoteles, zur Argumentationstheorie an der Schwelle vom Paradigma der Rhetorik und Topik zur formalen Logik sowie Informationen zum Verhältnis der Syllogistik zur Erkenntnistheorie, zum nicht-deduktiven Argumentieren und zur Semiotik.

KOMMENTAR

Kapitel 1

Das Thema von II 1 ist „mehreres Deduzieren“. Einen ersten Eindruck vermittelt § 9.1 der Einleitung. Das Kapitel weist Bezüge zu I 1–2 und I 4-6, insbesondere aber zu I 7 auf.

Mit „mehreres Deduzieren“ (vgl.

, 53a5) ist gemeint, dass sich in vielen Fällen aus dem Prämissenpaar einer assertorischen Deduktion mehr erschließen lässt als nur die Art von Konklusion, die in I 4–6 behandelt wurde. Das Thema wird in zwei Abschnitten behandelt:

(1) Der kurze Abschnitt 53a3–14 ist von großer systematischer Bedeutung für das Projekt der assertorischen Syllogistik. Insbesondere erlaubt er wichtige Rückschlüsse zur so genannten vierten Figur und zu den so genannten indirekten Deduktionen.

(2) Der längere Abschnitt 53a15–53b3 handelt davon, wie sich die Etablierung einer Konklusion auf Terme unter den Termen der Konklusion auswirkt. Anders als die Überleitung in 53a15 vermuten lässt, ist er von 53a3–14 sachlich unabhängig.

Der Behandlung des Themas von Kap. 1 voraus geht ein Vorspann (52b38– 53a3), der zusammenfasst, was für das Folgende als bereits abgehandelt vorausgesetzt wird (vgl. hierzu § 2.5). Ein Programm oder Plan für das zweite Buch wird am Ende des Vorspanns nicht festgehalten; es wird kein Vorhaben beschrieben, sondern es geht in 53a3 sogleich zur Sache.

Abschnitt 1 (52b38–53a3): Vorspann

52b38–39 „Wir sind bereits durchgegangen,

[i] in wie vielen Figuren [

] eine Deduktion [

] zustande kommt,

[ii] und durch welcherart und wie viele Prämissen [

] eine Deduktion zustande kommt,

[iii] und wann und wie dies geschieht.“

Im heute vorliegenden Text von Buch I werden die genannten Punkte in den Kapiteln I 1–2, I 4–6 (und I 23–26) gründlich durchgegangen. Wer diese Texte kennt, kann den ersten Satz mit seinen zentralen Fachwörtern „Deduktion“ (

), „Prämisse“ (

) und „Figur“ (

) deshalb verstehen, wer nicht, muss sie anderswo gelernt haben. Der Einleitungssatz hält die zur Lektüre von Buch II erforderlichen Vorkenntnisse fest. Ich bin daher, anders als Ebert und Nortmann, nicht der Ansicht, dass 52b38–535a3 an seinem überlieferten Ort „funktionslos“ (114) ist.

Der erste Satz von II 1 entspricht dem Fazit in I 26, 43a16–19 (Übersetzung aus Buch I hier und im Folgenden: Ebert/Nortmann):

„[i']Wie also jeder Syllogismus zustande kommt und

[ii'] aufgrund von wievielen Termini und Prämissen und in welchem Verhältnis diese zueinander stehen,

[iii'] weiterhin welche These in welcher Figur und welche in mehreren und welche in weniger (Figuren) bewiesen wird,

ist aus unseren Ausführungen klar geworden.“

Die Wendung „wann und wie“ (

, 52b39) findet sich im selben Kontext auch in der Aufgabenstellung von I 4–6 in I 4, 25b26 f. Als kleiner Einstufungstest gelesen, lautet II 1, 52b38–39:

a) Durch welcherart und wie viele Prämissen kommt eine Deduktion zustande?

b) In wie vielen Figuren?

c) Wann und wie?

Buch II setzt damit an Vorwissen den Inhalt der §§ 6.1–6.7 der Einleitung voraus.

Ad (a): „Wieviele Prämissen“? Mindestens zwei (§ 6.1). Die wahrheitserhaltende Transformation einer einzigen Prämisse (conversio), die in II 1, 53a3–14, thematisiert wird, gilt noch nicht als Deduktion (§ 6.4). II 17 und II 18, evtl. auch schon II 11–14, legen nahe, dass es Deduktionen mit mehr als zwei Prämissen gibt, wenngleich diese immer von solchen mit genau zwei Prämissen ausgehen.

„Welcherart sind die Prämissen?“ Alle Prämissen haben die Form XxY, und zwar XaY , XeY , XiY oder XoY (§ 6.2).

Ad (b): Die Antwort ist: in drei Figuren (§ 6.5).

Ad (c): Die Antwort auf diese Frage wird im Wesentlichen in I 4–6 gegeben (§ 6.6, 6.7). Aristoteles kommt immer wieder auf vierzehn prominente modi zurück, bei denen aus einem gegebenen Prämissenpaar eine Konklusion folgt (§ 6.6). Allerdings lässt schon I 7 erkennen, dass er diese Liste, wenn auch für alle Zwecke der Untersuchung vollständig, für nicht ganz abgeschlossen hält (§ 6.8). Die Einzelheiten werden im Zusammenhang mit 53a3–14 wichtig und im Kommentar dazu behandelt.

52b40–53a3 „[i] Ferner sind wir durchgegangen, auf welcherart Dinge man schauen muss, wenn man widerlegt oder etabliert und wie man ein vorliegendes 〈Problem〉 [

] im Rahmen einer jeden Untersuchung [

] angehen muss.

[ii] Ferner sind wir durchgegangen, auf welchem Wege wir die jeweiligen Ausgangspunkte [

] erhalten werden.“

Dies entspricht dem, was Aristoteles am Beginn von I 27, 43a21 f., als das Thema von I 27–30 festhält (vgl. hierzu auch Ebert/Nortmann, 111):

„Jetzt ist darzulegen,

[i'] wie wir selber es fertigbringen, immer eine ausreichende Anzahl Syllogismen für eine gegebene (These) zur Verfügung zu haben und

[ii'] auf welchem Wege wir die Prinzipien einer jeden (These) finden.“

Es soll also „ein Argumentierender in die Lage versetzt werden, […] zu einer vorgelegten These [=

] Prämissen zu finden, mit deren Hilfe sich diese These beweisen lässt.“ (Ebert/Nortmann, 109). Diese Aufgabe sieht Aristoteles am Ende von I 31 abgeschlossen. Es sei nun (I 31, 46b38-40)

„klar, woraus und wie die Beweise zustande kommen und nach welcherart (Bestimmungen) wir bei jeder (zu beweisenden) These Ausschau halten müssen.“

Die Phrase

(„im Rahmen einer jeden Untersuchung“) aus 53a1–2 findet sich ein weiteres Mal in II 23, 68b12, in vermutlich noch weiter zu nehmendem Sinne als hier.

Abschnitt 2 (53a3–14): auch noch Erschlossenes I (Konversionen, vierte Figur)

53a3–14 „Da die Deduktionen […] denn es kann allem zukommen.“

Der kurze Abschnitt enthält eine Fülle von Informationen von teils großer Bedeutung für das Projekt der assertorischen Syllogistik.

(1) „[D]ie Deduktionen [sind] teils allgemein […], teils partikulär…“ (53a3-4). Was genau ist hier mit allgemeinen, was mit partikulären Deduktionen gemeint? Naheliegend ist die folgende Definition:

(Variante 1) Eine Deduktion ist genau dann allgemein, wenn sie eine allgemeine (=universelle) Konklusion (a, e) hat, und genau dann partikulär, wenn sie eine...

Inhaltsverzeichnis

• Cover
• Titelseite
• Impressum
• Inhalt
• VORWORT
• ÜBERSETZUNG
• EINLEITUNG
• KOMMENTAR
• REGISTER