Quantenmechanik

Richard P. Feynman, Robert B. Leighton, Matthew Sands

• Verlag: De Gruyter Oldenbourg
• Jahr: 2015
• eBook-ISBN: 9783110398649
• Auflage: 6
• Thema: Naturwissenschaften
• Thema: Physik

In seinen legendären Vorlesungen aus dem Jahre 1965 ist es Richard P. Feynman gelungen, die Physik in einer leicht verständlichen Form darzustellen, ohne dabei auf Genauigkeit zu verzichten. Der didaktisch geschickte Aufbau hält den Leser bis zum Schluss gefesselt. Kein Wunder also, dass die Feynman Vorlesungen über Physik im Lehrbetrieb der Universitäten mittlerweile einen festen Platz eingenommen haben. Band 5 der New Millennium Edition vermittelt die Quantenmechanik. Feynman stellt dabei die physikalischen Ideen in den Vordergrund, eine umfassende Kenntnis der exakten mathematischen Grundlagen ist zum Verständnis nicht nötig. Das Buch eignet sich hervorragend zum Selbststudium als auch als Begleiter einer Vorlesung.

1 Quantenverhalten

Anmerkung: Dieses Kapitel stimmt nahezu mit Kapitel 12 des zweiten Bandes überein.

1.1 Mechanik in atomaren Dimensionen

„Quantenmechanik“ ist die Beschreibung des Verhaltens von Materie und Licht in allen Einzelheiten, insbesondere der Vorgänge in atomaren Dimensionen. In atomaren Dimensionen verhalten sich die Objekte überhaupt nicht so wie etwas, von dem wir direkte Erfahrung haben. Sie verhalten sich nicht wie Wellen, nicht wie Teilchen, nicht wie Wolken oder Billardkugeln, Gewichte an Federn oder irgendetwas, was wir je gesehen haben.

Newton dachte, das Licht bestehe aus Teilchen, doch dann entdeckte man, dass es sich wie eine Welle verhält. Später jedoch (zu Beginn des 20. Jahrhunderts) stellte man fest, dass sich das Licht tatsächlich manchmal wie ein Teilchen verhält. Ursprünglich glaubte man, das Elektron zum Beispiel verhielte sich wie ein Teilchen, dann aber erkannte man, dass es sich in vielerlei Hinsicht wie eine Welle verhält. In Wirklichkeit verhält es sich jedoch weder wie das eine noch wie das andere. Geben wir es also auf. Wir sagen: „Es ist wie keins von beiden.“

Wir haben jedoch Glück, denn die Elektronen verhalten sich genauso wie das Licht. Das Quantenverhalten von Objekten in atomaren Dimensionen (Elektronen, Protonen, Neutronen, Photonen usw.) ist für alle das gleiche, sie sind alle „Teilchenwellen“ oder wie auch immer man sie nennen möchte. Also ist das, was wir über die Eigenschaften des Elektrons (welches wir für unsere Beispiele heranziehen werden) kennenlernen, auch anwendbar auf alle „Teilchen“, einschließlich der Photonen des Lichts.

Die allmähliche Ansammlung von Informationen über das Verhalten im atomaren und mikroskopischen Bereich während des ersten Viertels des 20. Jahrhunderts, die uns einige Hinweise gaben, wie sich kleine Objekte verhalten, rief eine wachsende Verwirrung hervor, die schließlich 1926/27 von Schrödinger, Heisenberg und Born aufgelöst wurde. Ihnen gelang schließlich eine konsistente Beschreibung des Verhaltens von Materie im mikroskopischen Bereich. Wir werden die Hauptpunkte dieser Beschreibung in diesem Kapitel aufgreifen.

Weil das Verhalten der Atome so ganz außerhalb unserer normalen Erfahrung liegt, ist es sehr schwierig, sich daran zu gewöhnen, und es erscheint sowohl dem Neuling als auch dem erfahrenen Physiker seltsam und geheimnisvoll. Selbst die Experten verstehen es nicht so, wie sie es gerne möchten, und das ist nicht verwunderlich, da sich jede direkte menschliche Erfahrung und Intuition auf makroskopische Objekte bezieht. Wir wissen, wie sich große Objekte verhalten, aber die kleinen Objekte verhalten sich nicht so. Darum müssen wir unsere Erkenntnisse durch Abstraktion oder Imagination gewinnen und können nicht an unsere direkten Erfahrungen anknüpfen.

In diesem Kapitel werden wir sogleich das Grundelement dieses mysteriösen Verhaltens in seiner seltsamsten Form in Angriff nehmen. Zur Untersuchung wählen wir ein Phänomen aus, das auf klassische Art zu erklären absolut unmöglich ist und das in sich den Kern der Quantenmechanik birgt. Eigentlich enthält es das einzige Geheimnis. Wir können das Geheimnis nicht aufdecken, indem wir „erklären“, wie es funktioniert. Wir können nur berichten, wie es funktioniert, und indem wir dies tun, erörtern wir die grundlegenden Eigentümlichkeiten der ganzen Quantenmechanik.

1.2 Ein Experiment mit Kugeln

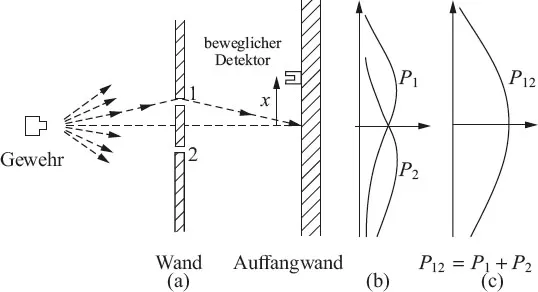
Wir werden versuchen, das Quantenverhalten von Elektronen zu verstehen, indem wir in einem speziellen Versuchsaufbau ihr Verhalten mit dem vertrauteren Verhalten von Teilchen, wie Kugeln, und Wellen, wie Wasserwellen, vergleichen und gegenüberstellen. Wir betrachten zuerst das Verhalten von Kugeln in dem in Abbildung 1.1 schematisch dargestellten Versuchsaufbau.

Abb. 1.1: Interferenzexperiment mit Kugeln.

Wir haben ein Maschinengewehr, das eine Salve von Kugeln abschießt. Es ist kein sehr gutes Gewehr, weil es die Kugeln wahllos über einen ziemlich großen Winkelbereich, wie im Bild gezeigt, verstreut. Vor dem Gewehr ist eine Wand (aus Panzerplatten), in der zwei Spalte sind, gerade groß genug, um eine Kugel hindurchzulassen. Hinter der Wand ist eine Auffangwand (sagen wir eine dicke Holzwand), die die Kugeln beim Auftreffen „absorbiert“. Vor der Auffangwand befindet sich ein Objekt, das wir „Detektor“ für Kugeln nennen wollen. Es könnte ein Kasten mit Sand sein. Jede Kugel, die in den Detektor eintritt, wird abgebremst und gespeichert. Wenn wir wollen, können wir den Kasten leeren und die Kugeln, die eingefangen wurden, zählen. Der Detektor kann hin und her bewegt werden (wir nehmen an in x-Richtung). Mit dieser Vorrichtung können wir experimentell die Antwort auf folgende Frage finden: „Wie groß ist die Wahrscheinlichkeit, dass eine Kugel, die durch die Spalte in der Wand geht, im Abstand x vom Mittelpunkt auf der Auffangwand ankommt?“ Zunächst sollten Sie einsehen, dass wir von Wahrscheinlichkeiten sprechen müssen, weil wir nicht mit Bestimmtheit sagen können, welchen Weg die individuelle Kugel nehmen wird. Eine Kugel, die zufällig einen der Spalte trifft, kann an dem Rand des Spalts abprallen und irgendwo auftreffen. Mit „Wahrscheinlichkeit“ meinen wir die Chance, dass eine Kugel im Detektor landet. Diese Chance können wir messen, indem wir die Kugeln zählen, die in einer bestimmten Zeiteinheit im Detektor ankommen, und dann das Verhältnis dieser Anzahl zur Gesamtzahl der in dieser Zeit auf der Auffangwand angekommenen Kugeln berechnen. Oder wenn wir annehmen, dass das Gewehr während der Messung immer im gleichen Zeitabstand schießt, ist die gesuchte Wahrscheinlichkeit direkt proportional zur Anzahl der Kugeln, die den Detektor in einem Standard-Zeitintervall erreichen.

Für unsere Zwecke wollen wir uns einen etwas idealisierten Versuch vorstellen, in welchem die Kugeln keine echten Kugeln, sondern unzerstörbare Kugeln sind – sie können nicht entzweibrechen. In unserem Versuch stellen wir fest, dass die Kugeln immer als Klumpen ankommen, und wenn wir etwas in dem Detektor finden, ist es immer eine ganze Kugel. Wenn der Zeitabstand, mit dem das Maschinengewehr feuert, stark verringert wird, sehen wir, dass zu irgendeinem gegebenen Moment entweder keine oder genau eine Kugel auf der Auffangwand ankommt. Auch ist die Größe des Klumpens sicherlich unabhängig von der Feuerfrequenz des Gewehrs. Wir sagen also: „Kugeln kommen immer als gleiche Klumpen an.“ Was wir mit unserem Detektor messen, ist die Wahrscheinlichkeit für das Ankommen eines Klumpens. Und wir messen die Wahrscheinlichkeit als Funktion von x. Das Ergebnis solcher Messungen mit diesem Apparat (wir haben das Experiment noch nicht durchgeführt, deshalb stellen wir uns das Ergebnis eigentlich nur vor) ist in Abbildung 1.1 (c) graphisch dargestellt. In der Zeichnung tragen wir die Wahrscheinlichkeit nach rechts und x vertikal auf, sodass die x-Skala zur Abbildung des Apparats passt. Wir nennen die Wahrscheinlichkeit P12, weil die Kugeln entweder durch Spalt 1 oder Spalt 2 gekommen sein können. Es wird Sie nicht überraschen, dass P12 zur Mitte des Diagramms hin groß ist, aber für sehr große x klein wird. Es mag jedoch verwundern, dass P12 den Maximalwert bei x = 0 hat. Diesen Sachverhalt können wir verstehen, wenn wir unser Experiment wiederholen und dabei einmal Spalt 2 und einmal Spalt 1 abdecken. Wenn Spalt 2 abgedeckt ist, können die Kugeln nur durch Spalt 1 gehen und wir erhalten die Kurve, die in Teil (b) der Abbildung mit P1 bezeichnet ist. Wie erwartet, tritt das Maximum von P1 bei dem x-Wert auf, der auf gerader Linie mit dem Gewehr und Spalt 1 liegt. Wenn Spalt 1 geschlossen ist, bekommen wir die symmetrische Kurve P2, die in der Abbildung eingezeichnet ist. P2 ist die Wahrscheinlichkeitsverteilung für Kugeln, die durch Spalt 2 hindurchgehen. Wenn wir die Teile (b) und (c) der Abbildung 1.1 vergleichen, finden wir als wichtiges Ergebnis

Die Wahrscheinlichkeiten addieren sich einfach. Der Effekt bei zwei geöffneten Spalten ist die Summe der Effekte, die bei je einem geöffneten Spalt auftreten. Wir werden dieses Resultat eine Beobachtung „ohne Interferenz“ nennen. Den Grund dafür werden Sie später verstehen. So viel über Kugeln. Sie kommen in Klumpen, und ihre Ankunftswahrscheinlichkeit zeigt keine Interferenz.

1.3 Ein Experiment mit Wellen

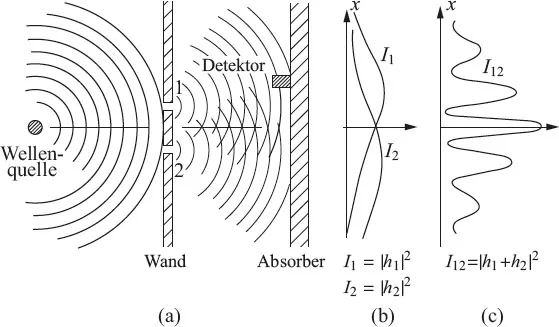
Jetzt wollen wir uns einen Versuch mit Wasserwellen ansehen. Die Vorrichtung ist in Abbildung 1.2 schematisch dargestellt. Wir verwenden ein flaches Gefäß mit Wasser. Ein kleiner Gegenstand, als „Wellenquelle“ bezeichnet, wird von einem Motor auf und nieder bewegt und erzeugt kreisförmige Wellen. Rechts von der Quelle befindet sich wieder eine Wand mit zwei Spalten, und dahinter ist eine zweite Wand, welche der Einfachheit halber ein „Absorber“ sei, sodass die Wellen, die dort ankommen, nicht reflektiert werden. Das kann man erreichen, indem man einen langsam ansteigenden „Sandstrand“ baut. Vor diesen Strand setzen wir einen Detektor, der wie zuvor in der x-Richtung hin und her bewegt werden kann. Der Detektor ist jetzt ein Gerät, das die „Intensität“ der Wellenbewegung misst. Man stelle sich eine raffinierte Vorrichtung vor, die die Höhe der Wellenbewegung ausmisst, deren Skala jedoch proportional zum Quadrat der ermittelten Höhe geeicht ist, sodass der abgelesene Wert proportional zur Intensität der Welle ist. Die Anzeige unseres Detektors ist dann proportional zur Energie, die von der Welle mitgeführt wird – oder richtiger: zur Energierate, die zum Detektor gelangt.

Abb. 1.2: Interferenzexperiment mit Wasserwellen.

Das Erste, was wir mit unserem Wellenapparat feststellen, i...

Inhaltsverzeichnis

• Cover
• Title
• Copyright
• Content
• 1 Quantenverhalten
• 2 Die Beziehung zwischen dem Wellen- und dem Teilchenbild
• 3 Wahrscheinlichkeitsamplituden
• 4 Identische Teilchen
• 5 Spin eins
• 6 Spin 1/2
• 7 Die Zeitabhängigkeit der Amplituden
• 8 Die Hamilton-Matrix
• 9 Der Ammoniak-Maser
• 10 Andere Zweizustandssysteme
• 11 Weitere Zweizustandssysteme
• 12 Die Hyperfeinaufspaltung im Wasserstoff
• 13 Ausbreitung im Kristallgitter
• 14 Halbleiter
• 15 Die Näherung unabhängiger Teilchen
• 16 Die Ortsabhängigkeit der Amplituden
• 17 Symmetrien und Erhaltungssätze
• 18 Drehimpuls
• 19 Das Wasserstoffatom und das Periodensystem
• 20 Operatoren
• 21 Die Schrödinger-Gleichung in einem klassischen Kontext
• Feynmans Epilog
• Index Band V
• Gesamtindex
• Personenverzeichnis
• Fußnoten