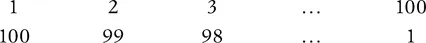Einstein & Associati

Il coworking della relatività

Elena Rinaldi

• Verlag: Hoepli
• Jahr: 2017
• ISBN:
  9788820379711
• Thema: Biological Sciences
• Thema: Science General

Chi erano i matematici che hanno lavorato con Einstein o i cui lavori hanno permesso la formulazione della teoria della relatività? Cosa sono le geometrie non euclidee e i tensori? Lo stesso Einstein più volte scrive nelle sue lettere che non sarebbe riuscito a completare il suo lavoro, costato fiumi di sudore, senza l'aiuto dei matematici che l'hanno preceduto e che l'hanno aiutato a correggere gli errori nella sua prima formulazione. Senza la scoperta di nuove geometrie da parte di Gauss e Riemann non potrebbe esistere l'idea di uno spazio curvo; senza i lavori di Ricci e Levi Civita la fisica non avrebbe potuto superare la teoria newtoniana. Viaggiando attraverso i concetti astratti della matematica si scopriranno alcune delle vite curiose dei protagonisti del pensiero scientifico del Novecento.

Capitolo 1

IL PRINCIPE DEI MATEMATICI

L’importanza di Gauss per lo sviluppo

della teoria fisica moderna e, soprattutto,

per i fondamenti matematici della teoria della relatività è

stata davvero determinante.

Albert Einstein

In una soleggiata giornata del 1818 un matematico poco più che quarantenne si accingeva a salire in vetta a uno dei monti del Regno di Hannover, nel Nord dell’attuale Germania. Il suo intento era quello di calcolare con la massima precisione possibile la distanza tra quella cima e altre due vette. Il matematico si chiamava Carl Friedrich Gauss ed era all’epoca conosciuto come uno dei geni viventi. Da undici anni dirigeva l’osservatorio dell’università di Göttingen, uno dei migliori centri scientifici del tempo, ed era stato incaricato dal re Giorgio III di mappare il Regno di Hannover, da pochi anni diventato indipendente. L’impresa non era per nulla semplice: bisognava per esempio calcolare con precisione la distanza tra punti che distavano diversi chilometri l’uno dall’altro, come le vette dei monti Hohenhagen, Inselberg e Brocken. Per effettuare quelle misurazioni Gauss pensò di far posizionare il suo assistente sulla cima del monte Brocken e di rilevarne la distanza osservandolo dalla vetta di Hohenhagen.

Figura 1.1 – Carl Friedrich Gauss.

Il problema principale era quello di vedere il compagno all’interno della foresta che ricopriva la vetta della montagna di fronte e, viceversa, di farsi vedere. Come fare?

Il matematico aveva pianificato la missione da tempo e nei mesi precedenti, chiuso nel suo studio dell’osservatorio di Göttingen, aveva notato che il rosone della chiesa di fronte era molto più visibile quando i raggi del sole si riflettevano sui vetri. Questa intuizione gli fece capire che se fosse riuscito a utilizzare i raggi del sole per farsi notare, l’assistente avrebbe potuto vederlo e rilevare la sua distanza. Analogamente avrebbe potuto fare l’altro.

Basandosi su questa idea, Gauss inventò e costruì un nuovo strumento, l’eliotropo, che permetteva di misurare grandi distanze con ampia precisione grazie a un telescopio sul quale era montato uno specchio piano che, muovendosi, rifletteva i raggi solari.

Figura 1.2 – Modello di eliotropo.

Il matematico si accorse ben presto che il suo strumento gli permetteva di misurare le distanze con maggiore facilità e precisione, grazie all’angolo di inclinazione dello specchio e agli ingrandimenti del telescopio, e così lo utilizzò per tutte le misurazioni.

Quello che Gauss non poteva immaginare era che l’intuizione di usare i raggi solari per comunicare la posizione di un oggetto o di un individuo avrebbe portato, nei secoli successivi, alla teoria dei segnali che ancora oggi ha importanti applicazioni militari e civili.

Dopo aver effettuato le misurazioni sulle tre cime, il matematico le riportò su una cartina geografica. Congiunse i tre punti a formare un triangolo e scrisse le misure sui lati. Ma, pur tenendo conto della sensibilità dello strumento e delle possibili imprecisioni di misura, i conti non tornavano. Gauss si accorse, infatti, che la lunghezza di un lato del triangolo non era maggiore della differenza degli altri due e minore della loro somma. Inoltre la somma degli angoli interni era leggermente superiore a 180°. Che cosa significava? Potevano esistere triangoli così fatti? La geometria euclidea lo vietava!

Eppure Gauss non aveva dubbi: quelle misure, che aveva così meticolosamente appuntato dal 1818 al 1832 in diverse parti del regno, erano esatte e qualsiasi triangolo di grandi dimensioni che veniva individuato sulla cartina e di cui venivano trovate le misure dei lati continuava a fornire la stessa caratteristica. Se si effettuavano misure di punti abbastanza vicini e si calcolavano le grandezze di triangoli piccoli questo non si verificava, o almeno non in modo così evidente, ma per triangoli grandi come quello formato dalle cime di Hohenhagen, Inselberg e Brocken non si avevano dubbi: non rispettavano i teoremi della geometria euclidea.

Figura 1.3 – Triangolazione delle tre cime di Hannover.

Gauss in un primo tempo era intimorito dalla possibilità che la geometria, che da secoli aveva guidato la conoscenza matematica, avrebbe potuto vacillare ma poi, come scrisse all’amico astronomo Olbers, si convinse che “l’onore della scienza richiede che si comprenda la natura di questa disuguaglianza in modo chiaro”. E così si mise con tutto se stesso a cercare di capire l’origine della peculiarità di quei triangoli.

Cercò di studiarli combinando metodi geometrici e algebrici. Capì fin da subito che utilizzare la geometria cartesiana comportava calcoli troppo complicati e talvolta equazioni irrisolvibili, pertanto pensò di introdurre un nuovo sistema per localizzare un punto sulla superficie terrestre e riportarlo sulla cartina geografica. Immaginò un insieme di curve che non si intersecano fra di loro e in grado di ricoprire tutta la superficie (detto anche un sistema di curve infinitamente denso). Poi considerò un secondo insieme di curve come quello precedente e che intersecasse il primo. In questo modo ciascun punto della superficie risultava stare su una curva del primo sistema e su un’altra del secondo. E viceversa, l’intersezione di due curve individuava sempre un punto. Questo nuovo metodo di localizzare i punti permise a Gauss di studiare i triangoli individuati nel corso delle sue misurazioni e si rivelò rivoluzionario nella storia del pensiero matematico, che fino ad allora aveva basato gli studi delle curve sulla geometria cartesiana. Il metodo di Gauss poteva essere applicato anche a spazi a tre, quattro o più dimensioni e divenne fondamentale per gli studi sulle stelle e sull’universo, in particolare nella formulazione della relatività. Il sistema di coordinate gaussiane, tuttavia, non confuta quello cartesiano, ma ne è una generalizzazione.

Grazie alle nuove coordinate e alle osservazioni sui triangoli, Gauss aveva capito che era possibile calcolare la curvatura di una qualsiasi superficie senza conoscerne la forma. Questo era un risultato senza precedenti, che Gauss formalizzò nel 1828 in un teorema, detto il teorema notevole (o Teorema Egregium), ancora oggi considerato uno dei più importanti risultati matematici perché permette di calcolare la curvatura di una superficie senza conoscerne intrinsecamente lo spazio. La curvatura gaussiana di una superficie, cioè la misura di quanto è curva in un punto, può essere determinata prendendo le misure direttamente sulla superficie, senza considerare lo spazio in cui essa è inserita.

Il teorema notevole, per esempio, può essere usato per dimostrare che una sfera non è una superficie piatta misurando lunghezze di lati e ampiezze di angoli sulla superficie della sfera. Gauss aveva capito che, poiché i triangoli che si formano su una superficie curva non soddisfano i teoremi e gli assiomi della geometria euclidea, potevano esistere “nuovi mondi matematici” nei quali bisognava ridefinire le distanze e le ampiezze, ripensare ai postulati e immaginare nuove figure. Decise tuttavia di tenere segrete queste sue considerazioni per timore delle “strida dei Beoti”, come definì egli stesso coloro che vedevano nella geometria euclidea l’unica in grado di descrivere la realtà.

Euclide e la geometria

Euclide nel primo libro degli Elementi diede alcune definizioni di enti primitivi geometrici quali la retta, il punto e il piano ed enunciò cinque postulati, cioè proposizioni che vengono considerate vere senza essere dimostrate. I postulati sono:

1.È possibile condurre una linea retta da un qualsiasi punto a ogni altro punto.

2.È possibile prolungare illimitatamente una retta finita in linea retta.

3.È possibile descrivere un cerchio con qualsiasi centro e distanza (raggio) qualsiasi.

4.Tutti gli angoli retti sono uguali fra loro.

5.Se, in un piano, una retta, intersecando due altre rette, forma con esse, da una medesima parte, angoli interni la cui somma è minore di due angoli retti, allora queste due rette, se indefinitamente prolungate, finiscono con l’incontrarsi dalla parte detta.

Da questi postulati Euclide ha dedotto tutti i teoremi della geometria euclidea, finendo con il teorema di Pitagora. Studiando e applicando le proposizioni di Euclide, gli studiosi cominciarono a interrogarsi sulla verità del quinto postulato che equivale ad affermare che, data una retta e un punto fuori da essa, esiste una e una sola retta parallela alla retta data e passante per il punto. L’affermazione, apparentemente ovvia, permette di dimostrare che in un triangolo la somma degli angoli interni è equivalente a due angoli retti. Questo è vero se si studia la geometria su una superficie piana, ma che cosa succede se si incurva il foglio?

Analizzando più nel dettaglio il postulato, i matematici cercarono di renderlo un teorema, cioè una verità dimostrata e non vera a priori, ma non ci riuscirono. Anche se si rivelò un’impresa non riuscita, la ricerca della dimostrazione del quinto postulato portò all’ipotesi teorica di nuove geometrie nelle quali possono per esempio esistere tante rette parallele a una data passanti per un punto (non appartenente alla retta).

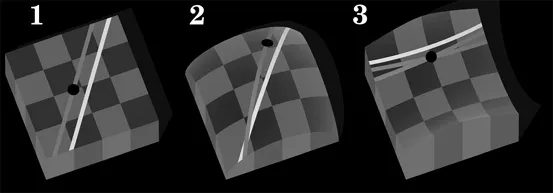
Figura 1.4 – Esempio di geometria euclidea in cui vale il quinto postulato (1), di geometria in cui non esistono rette parallele (2) e di geometria in cui è possibile tracciare più di una parallela (3).

Bambino prodigio

Quelle sulla geometria di una superficie non erano le prime intuizioni geniali di Carl Friedrich Gauss, che da bambino aveva dimostrato di possedere un’intelligenza superiore alla norma in diversi campi del sapere. Un aneddoto racconta che un giorno, mentre frequentava la scuola primaria, il maestro impose ai più turbolenti di calcolare la somma dei primi 100 numeri naturali e si diresse verso la porta per uscire dall’aula. Ma non fece in tempo ad afferrare la maniglia che il piccolo Carl appoggiò sulla cattedra la tavoletta dove aveva scritto la soluzione. Il maestro, sbigottito, si chiese come fosse possibile che un bambino di soli nove anni potesse svolgere in pochi minuti un tale calcolo e si consultò con il suo assistente.

Non si conosce il trucchetto ideato da Gauss per trovare il risultato in così breve tempo, ma si può ipotizzare che immaginò di disporre in riga i numeri da 1 a 100 e in una riga sottostante i numeri da 100 a 1.

Poi notò che la somma di tutte le coppie di numeri che venivano a formarsi in colonna dava 101. Poiché il numero delle coppie che avevano somma 101 era 100, moltiplicò 101 per 100. Si accorse, però, che ogni coppia aveva una gemella, infatti la coppia (1; 100) era uguale a (100; 1), la coppia (2; 99) era uguale a (99; 2) e così via; dunque bisognava dividere il risultato ottenuto per 2.

Oppure si può supporre che Gauss pensò ai numeri come puntini e li dispose l’uno ...