Discovering Group Theory

A Transition to Advanced Mathematics

Tony Barnard, Hugh Neill

• Verlag: CRC Press
• Jahr: 2016
• ISBN:
  9781315405766
• Auflage: 1
• Thema: Mathematics
• Thema: Algebra

Discovering Group Theory: A Transition to Advanced Mathematics presents the usual material that is found in a first course on groups and then does a bit more. The book is intended for students who find the kind of reasoning in abstract mathematics courses unfamiliar and need extra support in this transition to advanced mathematics.

The book gives a number of examples of groups and subgroups, including permutation groups, dihedral groups, and groups of integer residue classes. The book goes on to study cosets and finishes with the first isomorphism theorem.

Very little is assumed as background knowledge on the part of the reader. Some facility in algebraic manipulation is required, and a working knowledge of some of the properties of integers, such as knowing how to factorize integers into prime factors.

The book aims to help students with the transition from concrete to abstract mathematical thinking.

1

Proof

1.1 The Need for Proof

Proof is the essence of mathematics. It is a subject in which you build secure foundations, and from these foundations, by reasoning, deduction, and proof, you deduce other facts and results that you then know are true, not just for a few special cases, but always.

For example, suppose you notice that when you multiply three consecutive whole numbers such as 1 × 2 × 3 = 6, 2 × 3 × 4 = 24, and 20 × 21 × 22 = 9240, the result is always a multiple of 6. You may make a conjecture that the product of three consecutive whole numbers is always a multiple of 6, and you can check it for a large number of cases. However, you cannot assert correctly that the product of three consecutive whole numbers is always a multiple of 6 until you have provided a convincing argument that it is true no matter which three consecutive numbers you take.

For this example, a proof may consist of noting that if you have three consecutive whole numbers, one (at least) must be a multiple of 2 and one must be a multiple of 3, so the product is always a multiple of 6. This statement is now proved true whatever whole number you start with.

Arguing from particular cases does not constitute a proof. The only way that you can prove a statement by arguing from particular cases is by ensuring that you have examined every possible case. Clearly, when there are infinitely many possibilities, this cannot be done by examining each one in turn.

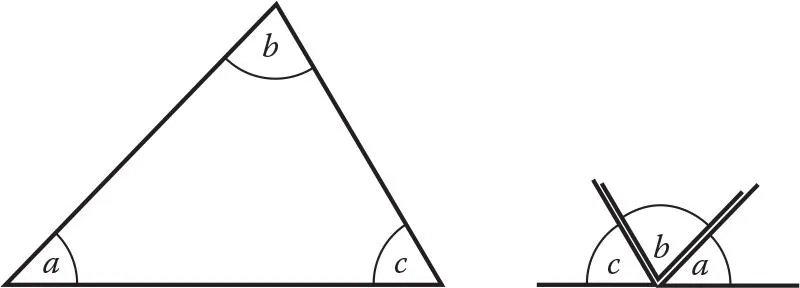
Similarly, young children will “prove” that the angles of a triangle add up to 180° by cutting the corners of a triangle and showing that if they are placed together as in Figure 1.1 they make a straight line, or they might measure the angles of a triangle and add them up. However, even allowing for inaccuracies of measuring, neither of these methods constitutes a proof; by their very nature, they cannot show that the angle sum of a triangle is 180° for all possible triangles.

So a proof must demonstrate that a statement is true in all cases. The onus is on the prover to demonstrate that the statement is true. The argument that “I cannot find any examples for which it doesn’t work, therefore it must be true” simply isn’t good enough.

FIGURE 1.1
“Proof” that the angles of a triangle add to 180°.

Here are two examples of statements and proofs.

EXAMPLE 1.1.1

Prove that the sum of two consecutive whole numbers is odd.

Proof

Suppose that n is the smaller whole number. Then (n + 1) is the larger number, and their sum is n + (n + 1) = 2n + 1. Since this is one more than a multiple of 2, it is odd. ■

The symbol ■ is there to show that the proof is complete. Sometimes, in the absence of such a symbol, it may not be clear where a proof finishes and subsequent text takes over.

EXAMPLE 1.1.2

Prove that if a and b are even numbers, then a + b is even.

Proof

If a is even, then it can be written in the form a = 2m where m is a whole number. Similarly b = 2n where n is a whole number. Then a + b = 2m + 2n = 2(m + n). Since m and n are whole numbers, so is m + n; therefore a + b is an even number. ■

Notice in Example 1.1.2 that the statement says nothing about the result a + b when a and b are not both even. It simply makes no comment on any of the three cases: (1) a is even and b is odd; (2) a is odd and b is even; and (3) a and b are both odd.

In fact, a + b is even in case (3) but the statement of Example 1.1.2 says nothing about case (3).

The same is true of general statements made in everyday life. Suppose that the statement: “If it is raining then I shall wear my raincoat” is true. This statement says nothing about what I wear if it is not raining. I might wear my raincoat, especially if it is cold or it looks like rain, or I might not.

This shows an important point about statements and proof. If you are proving the truth of a statement such as “If P then Q,” where P and Q are statements such as “a and b are even” and “a + b is even,” you cannot deduce anything at all about the truth or falsity of Q if the statement P is not true.

1.2 Proving by Contradiction

Sometimes it can be difficult to see how to proceed with a direct proof of a statement, and ...