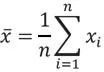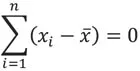Multiple lineare Regression & High Performance Computing

Methodik und Software-Implementation komplexer Analysemodelle

Thomas Kaul

• Verlag: Books on Demand
• Jahr: 2015
• ISBN drucken: 9783734743610
• eBook-ISBN: 9783738669497
• Auflage: 4
• Thema: Informatik
• Thema: Informationstechnologie

Dieses Buch hat zum Ziel, die in der empirischen Forschung häufig verwendete Methode der multiplen linearen Regressionsanalyse in nachvollziehbarer Weise darzulegen. Als Hilfsmittel hierfür wird die schrittweise Entwicklung einer leistungsfähigen Software mit der weitverbreiteten Programmiersprache C unter Rückgriff auf Konzepte der parallelen Programmierung und des Cluster Computing herangezogen. Hierzu werden zunächst relevante mathematische Zusammenhänge aufgegriffen, die auch ohne größere Vorkenntnisse für den Leser nachvollziehbar sein sollten.Es werden Betrachtungen zur Effizienz von Algorithmen vorgenommen, welche für die Analyse von komplexen Modellen und von umfangreichen Datenmengen ("big data") unabdingbar sind. Im Buch wird anschaulich erläutert, wie die Berechnung eines komplexen Prognosemodells mit 20 Eingangsvariablen -abhängig von der konkreten Software-Implementation- entweder über 8000 Jahre oder unter 8 Minuten Rechenzeit benötigt. Beispielhaft werden mit der erstellten Analysesoftware empirische Daten einer vom Autor im Sommer 2014 durchgeführten psychologischen Feldstudie zur Burnout-Forschung an Beschäftigten im deutschen Gesundheitswesen untersucht.Das Buch integriert methodische Ansätze aus den Disziplinen Informatik und Psychologie und enthält 72 Tabellen, 67 Abbildungen sowie 45 Formeln.

1. Über dieses Buch

für meine Frau Gesa

Dieses Buch hat zum Ziel, die in der empirischen Forschung häufig verwendete Methode der multiplen linearen Regressionsanalyse in nachvollziehbarer Weise darzulegen. Als Hilfsmittel hierfür wird die schrittweise Entwicklung einer performanten Software mit der weitverbreiteten Programmiersprache C unter Rückgriff auf Konzepte der parallelen Programmierung und des Cluster Computing herangezogen. Hierzu werden zunächst relevante mathematische Zusammenhänge aufgegriffen, die auch ohne größere Vorkenntnisse für den Leser nachvollziehbar sein sollten.

Es werden Betrachtungen zur Effizienz von Algorithmen vorgenommen, welche für die Analyse von komplexen Modellen und von umfangreichen Datenmengen („big data“) unabdingbar sind. Im Buch wird anschaulich erläutert, wie die Berechnung eines komplexen Prognosemodells mit 20 Eingangsvariablen -abhängig von der konkreten Software-Implementation- entweder über 8000 Jahre oder unter 8 Minuten Rechenzeit benötigt. Beispielhaft werden mit der erstellten Analysesoftware empirische Daten einer vom Autor im Sommer 2014 durchgeführten psychologischen Feldstudie zur Burnout-Forschung an Beschäftigten im deutschen Gesundheitswesen untersucht.

Das Buch integriert methodische Ansätze aus den Disziplinen Informatik und Psychologie und enthält 72 Tabellen, 67 Abbildungen sowie 45 Formeln.

Anmerkungen zur 5.Auflage

Zur weiteren Laufzeitoptimierung wurde eine zusätzliche Parallelisierung der Hauptregressionsanalyse auf im Cluster verfügbare Computer mit Mehrkernprozessoren umgesetzt (Kap. 5.14). Mit dem zusätzlich vorgenommenen Experiment 9 konnten nunmehr weitere Performanzgewinne von zusätzlich 35% nachgewiesen werden. Dabei wurde z.B. die Berechnung eines komplexen Regressionsmodells mit 20 Prädiktoren in einer Durchlaufzeit von weniger als acht Minuten auf einer experimentellen Clusterumgebung mit 16 verfügbaren Prozessorkernen abgeschlossen. Diese Performanzgewinne ermöglichten die Simulation hochkompexer Regressionsmodelle mit 24 Prädiktoren mit einer Durchlaufzeit von weniger als neun Stunden. In methodischer Hinsicht erfolgte im Kap. 4.4 eine Berücksichtigung der Modelldiagnose von Residuen und Mahalonobis-Distanzen. Anhand eines konkreten Beispiels wurden die Auswirkungen von Ausreißern und einflussreicher Datenpunkte auf die Parameterschätzungen und die Modellpassung einer Regressionsanalyse veranschaulicht. Im Kap. 4.5 wurde das Bootstrapping-Verfahren anhand eines nachvollziehbaren Beispiels eingearbeitet und die Grundlage zur späteren Anwendung dieser Technik in der multiplen linearen Regression gelegt.

Zudem wurde im Kap. 5.16 eine vergleichende Betrachtung zwischen verschiedenen C-Compilern und deren Auswirkungen auf die Performance der Software eingearbeitet und experimentell nachvollzogen.

Dätgen, im April 2015

Anmerkungen zur 4.Auflage

Als weitere Ergänzung wurde das Konzept des Cluster Computing im Kap. 5.14 berücksichtigt. Die vorgestellte Software-Lösung wurde um ein simples Protokoll zur Rechnerkommunikation im Cluster in Kombination mit paralleler Ausführung auf beteiligten Mehrkern-Prozessoren erweitert. Im Zuge dessen wird auch die Lastverteilungs-Problematik näher diskutiert.

Anmerkungen zur 3.Auflage

Mit der 3.Auflage erfolgte eine weitere Optimierung der Software zur effizienten Berechnung komplexer Regressionsmodelle und damit einhergehend eine Erweiterung des Kapitels 5.9. Zudem wurde in Kap.0 ein weiterer Hypothesentest der zugrundeliegenden Studie aufgenommen. Im Anhang A-8 wurde zusätzlich eine um eine simple Dateiverwaltung erweiterte Softwareversion aufgenommen, welche eine wiederholte Eingabe von Messdaten überflüssig macht.

Anmerkungen zur 2.Auflage

In der 2.Auflage erfolgte eine Überarbeitung von Kap. 2.4 mit genaueren Erläuterungen zur linearen Transformation von Matrizen. Zudem wurde das Kap. 5.10 und der Anhang A-6 mit optimierten Programmroutinen zur linearen Transformation von Matrizen und zur Berechnung von Determinanten aktualisiert. Der Abschnitt zur praktischen Anwendung der multiplen linearen Regression (Kap.0) wurde um die Prüfung einer weiteren Hypothese aus der zugrundeliegenden Studie ergänzt.

2. Ausgewählte mathematische Grundlagen

Mit korrelativen Analysen können lediglich ungerichtete Zusammenhänge zwischen Merkmalen untersucht werden. Sachlogische Überlegungen können jedoch häufig eine Richtung der Beeinflussung nahelegen (Fahrmeir, Künstler, Pigeot & Tutz, 2007, S. 153). In der Regressionsanalyse muß entschieden werden, welche Variablen (die sog. Prädiktoren, meist mit X_i bezeichnet) welche Variable (das sog. Kriterium, meist mit Y bezeichnet) vorhersagen sollen (Sedlmeier & Renkewitz, 2013, S.237).

Für die lineare Regressionsanalyse sind ausgewählte mathematische Grundlagen von Bedeutung. Aus der deskriptiven Statistik werden sowohl univariate Maße (auf ein Merkmal bezogen), bivariate Maße (auf zwei Merkmale bezogen), als auch multivariate Maße (auf mehr als zwei Merkmale bezogen) benötigt.

2.1. Univariate Maße

Das arithmetische Mittel aus n vorliegenden Messwerten x_i (der sog. Urliste) ist in Formel 1 für metrische Merkmale definiert (Fahrmeir et al., 2007, S. 53-54). Bedeutsam für die lineare Regression ist die Schwerpunkteigenschaft des arithmetischen Mittels, d.h. alle Abweichungen der einzelnen Messwerte von ihrem gemeinsamen Mittelwert heben sich zu Null auf (vgl. hierzu die Formel 2).

Formel 1: Arithmetisches Mittel

Formel 2: Schwerpunkteigenschaft des arithmetischen Mittels

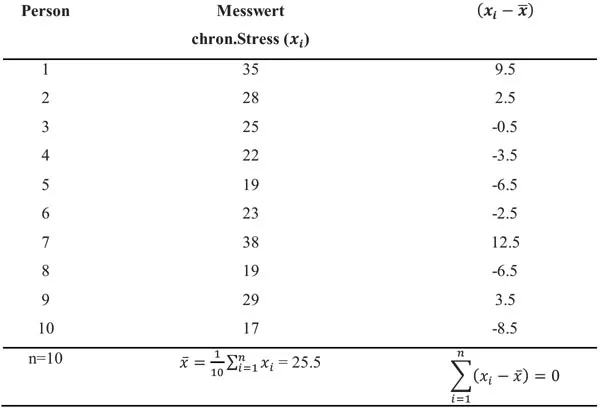
Beispiel. Messreihe zum chronischen Stress von zehn Probanden.

Tabelle 1 Das arithmetische Mittel zu realen Messdaten

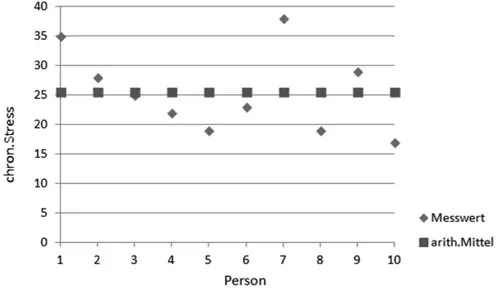
Abbildung 1: Messreihe zum chronischen Stress.

Tabelle 1 und Abbildung 1 demonstrieren anschaulich die Schwerpunkteigenschaft des arithmetischen Mittels. Die Messwerte einzelner Personen weichen mehr oder weniger vom aus allen Personen errechneten Mittelwert ab. Dabei heben sich die Über- und Unterschreitungen der Einzelpersonen vom Mittelwert zu Null auf.

Eine weitere, für die lineare Regression bedeutsame univariate Kenngröße ist die Streuung der Messwerte eines Merkmals, die empirische Varianz. Sie steht im Zusammenhang mit dem arithmetischen Mittel und ist nur für metrische Merkmale sinnvoll einsetzbar (Fahrmeir et al., 2007, Kap. 2.2.3). Es ist wichtig festzuhalten, daß die empirische Varianz (Formel 3) aus der mittleren quadrierte...

Inhaltsverzeichnis

• Über den Autor
• Inhaltsverzeichnis
• Abkürzungsverzeichnis
• Tabellenverzeichnis
• Abbildungsverzeichnis
• Formelverzeichnis
• 1. Über dieses Buch
• 2. Ausgewählte mathematische Grundlagen
• 3. Das einfache lineare Regressionsmodell
• 4. Das multiple lineare Regressionsmodell
• 5. Software-Implementation
• 6. Ein praktischer Anwendungsfall
• Literaturverzeichnis
• Anhang
• Impressum