Quantenmechanik aus elementarer Sicht Buch 2

Karl Fischer

• Verlag: Books on Demand
• Jahr: 2013
• ISBN drucken: 9783732243556
• eBook-ISBN: 9783732209408
• Auflage: 1
• Thema: Biological Sciences
• Thema: Science General

Das Buch bringt die Euler-Lagrange-Gleichungen klassisch und für die QM, das Schrödinger-Näherungs-Verfahren z.B. für den anharmonischen Oszillator, QM-typische komplizierte Integrationsmethoden, die Streuung ohne und mit Feldoperatoren, nicht-euklidische Geometrie im Hinblick auf die Gravitationstheorie, Young-Diagramme, indefinite Metrik dazu die regularisierte Zweipunktfunktion, Primzahlsätze und vieles mehr und zu allem viele Beispiele.

1.0 Variationsrechnung, Eulergleichungen, Lagrangefunktionen

1.1 Allgemeines, die Brachistochrone

Die Variationsrechnung sei gleich an einem Beispiel illustriert.

Ein Körper soll in einer senkrecht gedachten Ebene von der Stelle x=0, y=0 ausgehend zur Stelle x=h, y=a reibungsfrei gleiten. Gefragt ist nach dem Kurvenverlauf y(x), bei dem er am schnellsten zum Ziel kommt.

(griech. brachistos chronos kürzeste Zeit)

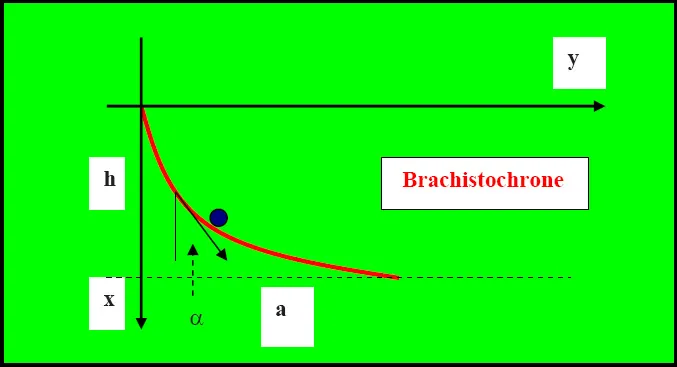
Das (x,y)-Koordinatensystem ist gegenüber dem gewöhnlichen Zeichnen um 90Grad im Uhrzeigersinn gedreht. Die Schwere zeigt so nach unten.

Wäre es in Normalanordnung, also zurückgedreht, so würde die Kurve einem Parabelzweig ähneln und die Schwerkraft würde nach rechts ziehen, was die Anschauung strapaziert, aber äquivalent ist.

Für ein kleines Wegstück ds auf der Bahn braucht der Körper die Zeit

dt = ds/v, wenn v die aktuelle Geschwindigkeit ist.

Nun ist ds² = dx² + dy² = [1 + (dy/dx)²]*dx², also ds = (1+y´²)^1/2 * dx

Dabei ist y´ = dy/dx der Differentialquotient von y

Die aktuelle Geschwindigkeit v ergibt sich aus dem Energiesatz:

mv²/2 = mg*x Kinetische Energie = aufgebrauchte potentielle Energie. Daraus folgt unmittelbar v = [2gx]^1/2

Wir haben also

Mit diesem Integral kann man die Laufzeit berechnen, wenn der Kurvenverlauf y(x) bzw y´(x) bekannt ist. Das gilt also allgemein.

Wir gehen einen Schritt weiter. Wir wollen durch Variation des Integrals den Kurvenverlauf mit der Minmaleigenschaft, im Beispiel die Zeit, erst ermitteln.

-------------------------------------------------------------------

Variation: Um nun den Bahnverlauf y(x) zu finden, wird der Integrand, nennen wir ihn allgemein A(y, y´,x) variiert:

Angenommen der Kurvenverlauf wäre etwas anders, also y(x) => y(x) + δy(x), wobei die kleine Funktion δy(x) die Abweichung von y(x) ausdrückt, dann ist die Ableitung der geänderten Funktion gleich (y(x)+ δy(x))´ = y´(x)+δy´(x).

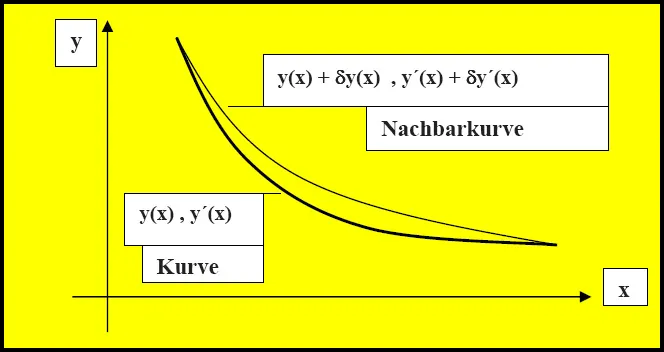
Es ist erlaubt, nach solchen Komplexen wie y und y´partiell zu differentieren.

Das ist analog zur Kettenregel.

Für die Änderung von A, als Funktion von y, y´und x, gilt dann analog zur Taylorreihe, in erster Ordnung:

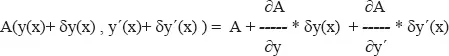
δy´(x) ist also nicht unabhängig, sondern ist die Ableitung von δ(x), also δy´(x) = dδy(x)/dx.

Die Änderung von A, namentlich δA, kommt also nicht dadurch zu Stande, dass sich x ändert, sondern, dass bei gleichem x die Funktion A

hinsichtlich ihrer Argumente y bzw y´ um einen Betrag δy bzw δy´ verändert, variiert wird. Deswegen tritt auch ∂A/∂x bei δA nicht auf.

-------------------------------------------------------------------

Die Änderung des Integrals ist also

-------------------------------------------------------------------

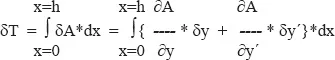
Es ist nun weiterführend, wenn man im zweiten Term partiell die Kleinfunktion δy´ integriert

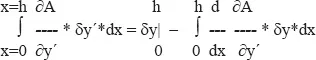
Da die Funktion y(x) gewissermaßen an den Enden festgezurrt ist, siehe Bild, ist an diesen Stellen δy(h) = δy(0) = 0, somit ist der erste Teil = 0.

---------------------------------------------------------------------------------

Und es verbleibt

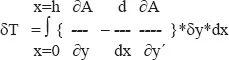
Wenn nun y(x) so ist, dass das Gesamtintegral T minimal (oder maximal) ist, so muss δT =0 sein. Da δy klein, aber beliebig ist, hat das zur Folge, dass der {…}-Ausdruck gleich 0 sein muss, also

-------------------------------------------------------------------

-------------------------------------------------------------------

In unserem Beispiel ist

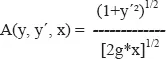
Da y in A explizit nicht vorkommt, ist ∂A/∂y = 0

Es ist ∂A/∂y´ = ½*(1+y´²)^-1/2 *2y´ * [2gx]^-1/2

Die verbleibende Variations-Gleichung ist also d/dx[∂A/∂y´] = 0, man kann [2g]^-1/2 wegkürzen, sie kann fürs erste bezüglich x sofort integriert werden. Man erhält [∂A/∂y´] = C eine Konstante, konkret hier

-------------------------------------------------------------------------

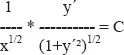
Zu ihrer Lösung, zur Bestimmung von y, substituiert man nun y´ = tanα α ist also jeweils der Steigungswinkel der Kurventangente zur x-Achse Nun ist tanα = sinα/cosα,

deshalb ist (1+y´²)^1/2 = 1/cosα und y´/(1+y´²...

Inhaltsverzeichnis

• Titelseite
• Widmung
• Inhaltsverzeichnis
• Einleitung
• 1.0 Variationsrechnung, Eulergleichungen, Lagrangefunktionen
• 2.0 Das Schrödinger-Näherungsverfahren mit Eigenwerten
• 3.0 Die Dipolstrahlung
• 4.0 Interessante Integrale und Integrationsmethoden
• 5.0 Beispiel: Zweite Bornsche Näherung beim Yukawa-Potential
• 6.0 Streuung, relativistisch
• 7.0 Relativistische Kinematik
• 8.0 Geometrie und Physik im Nichteuklidischen
• 9.0 Betrachtungen über die indefintite Metrik
• 10.0 Über Schiebeoperatoren und Young-Diagramme
• 11.0 Betrachtungen über Primzahlen, Wahrscheinlichkeit, Primzahlsatz
• 12.0 Kleinere Themen
• Stichwortverzeichnis
• Literaturverzeichnis
• Über den Autor
• Impressum