In diesem Buch werden die drei großen Themengebiete der Mathematik in der Oberstufe, die Analysis, die analytische Geometrie bzw. lineare Algebra und die Stochastik zusammengefasst. Dabei wird alles mit vielen Beispielen und Abbildungen erklärt. Die Beschreibungen orientieren sich an den Aufgaben- und Problemstellungen, wie sie in der Oberstufe an Gymnasien als auch an Fachoberschulen behandelt werden. Das Buch kann auch zur Abiturvorbereitung verwendet werden oder zum selbstständigen Aufarbeiten des Stoffes der Oberstufe beispielsweise vor einem Studium. Es wurden viele Erklärungen, wichtige Hinweise für bestimmte Aufgabentypen, Aufgabenbeispiele mit Lösungstipps und Grafiken eingefügt. Bei allen Beschreibungen wurde darauf geachtet, dass diese für Schülerinnen und Schüler möglichst verständlich sind. Die Grafiken und auch die meisten hier beschriebenen Methoden können mit der Seite www.alles-mathe.de erstellt bzw. angewendet werden, um beispielsweise eigene Lösungen von Aufgaben zu überprüfen oder auch mal um eine Wertetabelle zu erstellen. Weitere Aufgaben, Beispiele und Erklärungen zum Buch sind auf der Seite www.mathe-total.de zu finden. Da dieses Buch drei Bücher von mir zu den einzelnen Themengebieten umfasst, besteht es aus drei Teilen. Begonnen wird im ersten Teil mit der Analysis, gefolgt von der analytischen Geometrie im zweiten Teil und der letzte dritte Teil befasst sich mit der Stochastik. In der aktuellen Auflage wurden Links zu Übungsaufgaben mit Lösungen und Erklärungen ergänzt.
Häufig gestellte Fragen
Ja, du kannst dein Abo jederzeit über den Tab Abo in deinen Kontoeinstellungen auf der Perlego-Website kündigen. Dein Abo bleibt bis zum Ende deines aktuellen Abrechnungszeitraums aktiv. Erfahre, wie du dein Abo kündigen kannst.
Derzeit stehen all unsere auf mobile Endgeräte reagierenden ePub-Bücher zum Download über die App zur Verfügung. Die meisten unserer PDFs stehen ebenfalls zum Download bereit; wir arbeiten daran, auch die übrigen PDFs zum Download anzubieten, bei denen dies aktuell noch nicht möglich ist. Weitere Informationen hier.
Perlego bietet zwei Pläne an: Elementar and Erweitert
Elementar ist ideal für Lernende und Interessierte, die gerne eine Vielzahl von Themen erkunden. Greife auf die Elementar-Bibliothek mit über 800.000 professionellen Titeln und Bestsellern aus den Bereichen Wirtschaft, Persönlichkeitsentwicklung und Geisteswissenschaften zu. Mit unbegrenzter Lesezeit und Standard-Vorlesefunktion.
Erweitert: Perfekt für Fortgeschrittene Studenten und Akademiker, die uneingeschränkten Zugriff benötigen. Schalte über 1,4 Mio. Bücher in Hunderten von Fachgebieten frei. Der Erweitert-Plan enthält außerdem fortgeschrittene Funktionen wie Premium Read Aloud und Research Assistant.
Beide Pläne können monatlich, alle 4 Monate oder jährlich abgerechnet werden.
Wir sind ein Online-Abodienst für Lehrbücher, bei dem du für weniger als den Preis eines einzelnen Buches pro Monat Zugang zu einer ganzen Online-Bibliothek erhältst. Mit über 1 Million Büchern zu über 1.000 verschiedenen Themen haben wir bestimmt alles, was du brauchst! Weitere Informationen hier.
Achte auf das Symbol zum Vorlesen in deinem nächsten Buch, um zu sehen, ob du es dir auch anhören kannst. Bei diesem Tool wird dir Text laut vorgelesen, wobei der Text beim Vorlesen auch grafisch hervorgehoben wird. Du kannst das Vorlesen jederzeit anhalten, beschleunigen und verlangsamen. Weitere Informationen hier.
Ja! Du kannst die Perlego-App sowohl auf iOS- als auch auf Android-Geräten verwenden, um jederzeit und überall zu lesen – sogar offline. Perfekt für den Weg zur Arbeit oder wenn du unterwegs bist. Bitte beachte, dass wir keine Geräte unterstützen können, die mit iOS 13 oder Android 7 oder früheren Versionen laufen. Lerne mehr über die Nutzung der App.
Ja, du hast Zugang zu Jetzt lerne ich Mathematik für die Oberstufe von Marco Schuchmann im PDF- und/oder ePub-Format sowie zu anderen beliebten Büchern aus Mathematics & Higher Education. Aus unserem Katalog stehen dir über 1 Million Bücher zur Verfügung.
Die waagrechte Achse ist im Folgenden immer die x-Achse (Abszisse) und die senkrechte Achse die y-Achse (Ordinate).
m ist die Steigung. Wenn x um eines erhöht wird, dann erhöht oder verringert sich f(x) um m, je nachdem, ob m positiv oder negativ ist (denn f(x+1) - f(x) = m). Wenn m = 0 ist, dann ist die Gerade eine parallele zur x-Achse und für b = 0 liegt diese auf der x-Achse. b ist der Achsenabschnitt auf der y-Achse (kurz: y-Achsenabschnitt). D.h. die Gerade scheidet die y-Achse im Punkt Sy(0; b), denn f(0) = b. Die Nullstelle ist der Schnittpunkt mit der x-Achse. Da alle Punkte, die auf der x-Achse liegen, die y-Koordinate Null haben, muss man zur Berechnung der Nullstellen die Funktionsgleichung gleich Null setzen.
Nullstellen bestimmen:
Es sei m ≠ 0
f(x) = mx + b = 0 | -b
mx = -b
x = -b/m.
Also ist x = -b/m die Nullstelle der Gerade, bzw. N(-b/m; 0) deren Schnittpunkt mit der x-Achse.
Beispiel:
Gegeben ist die Geradengleichung f(x) = -2x + 4. Gesucht sind die Schnittpunkte mit den Koordinatenachsen.
Mit der y-Achse: Sy(0; 4)
Mit der x-Achse: -2x + 4 = 0 | -4
-2x = -4 | :(-2)
x = 2 ⇒ N(2; 0)
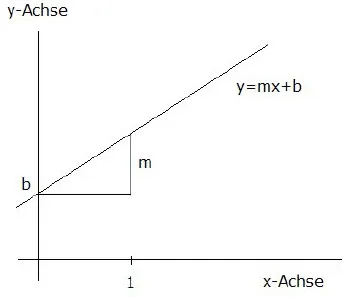
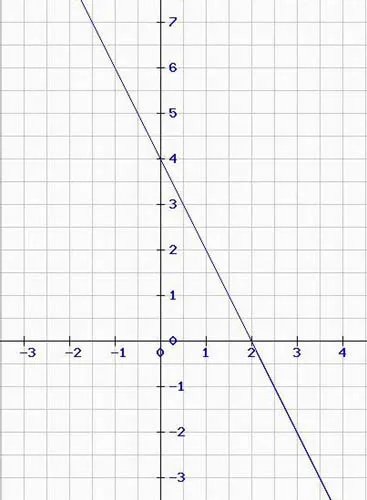
1.1.2 Bestimmung der Geradengleichung
Gegeben seien zwei Punkte P(x1; y1) und Q(x2; y2) und gesucht ist die Gleichung der Geraden durch diese zwei Punkte.
Beispiel:
Gegeben sind die Punkte P(-2; 4) und Q(1; 10). Gesucht ist die Gleichung der Geraden durch diese Punkte.
Eine Möglichkeit die Gleichung zu bestimmen, wäre die, die Komponenten der beiden Punkte in die Funktion f(x) = mx + b einzusetzen. Diese Möglichkeit funktioniert auch bei anderen Funktionstypen und man muss sich keine Formel merken:
(1) f(-2) = -2m + b = 4
(2) f(1) = m + b = 10
Es handelt sich hier um ein Gleichungssystem mit zwei Unbekannten.
Subtrahiert man die Gleichung (1) von der Gleichung (2), so „fällt b weg“:
(1) - (2) -3m = -6 |: (-3)
m = 2
Setzt man m = 2 z.B. in (2) ein, so ergibt sich
2 + b = 10 | -2
b = 8
Damit lautet die Gleichung: f(x) = 2x + 8
Man könnte die Gleichung auch mit folgenden Formeln bestimmen:
(I) f(x) = m(x – x1) + y1 mit m =
Würde man die Formel im Beispiel von oben verwenden, so gilt:
f(x) = 2(x - (-2)) + 4 = 2x + 8
Statt zwei Punkten könnte auch ein Punkt P(x1; y1) und die Steigung m gegeben sein. In diesem Fall kann man m und die Koordinaten des Punktes P direkt in (I) einsetzen.
Ein weiteres Beispiel:
Gegeben ist die Gleichung f(x) = 2x + 2 der Geraden f.
a) Liegt P(1; 4) auf der Geraden f?
f(1) = 2 + 2 = 4, womit P auf der Geraden liegt.
b) Bestimme die fehlenden Koordinaten der Punkte Q(3;?) und R(?; -4) auf der Geraden f.
f(3) = 6 + 2 = 8 ⇒ Q(3; 8)
f(x) = 2x + 2 = -4 | -2
2x = -6 | :2
x = -3, also ist R(-3; -4).
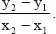
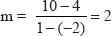
1.1.3 Schnittpunkte und Schnittwinkel
Stimmen die Steigungen zweier Geraden überein, so sind diese parallel zueinander. Sind die Achsenabschnitte verschieden, dann sind sie „echt parallel“ und haben auch keinen Schnittpunkt.
Schnittstellen bestimmt man allgemein durch Gleichsetzten beider Funktionsgleichungen.
Beispiel:
f(x) = 2x + 4
g(x) = -x + 1
f(x) = g(x)
2x + 4 = -x + 1 | +x
3x + 4 = 1 | -4
3x = -3 | :3
x = -1
Nun kann man den y-Wert des Schnittpunktes bestimmen, indem man x = -1 in eine der beiden Geradengleichungen einsetzt:
y = g(-1) = -(-1) + 1 = 2
Also ist S(-1; 2) der Schnittpunkt.
Kommen wir nun zur Berechnung des Schnittwinkels:
Der Neigungswinkel einer Geraden y = mx + b in Bezug zur x-Achse ergibt sich durch folgende Gleichung:
m = tan(α)
Hier kann sich auch ein negativer Wert für α ergeben, falls die Gerade eine negative Steigung hat. In diesem Fall ergibt sich die Gerade durch Drehung der x-Achse in negativer Drehrichtung (d.h. mit dem Uhrzeigersinn) um die Nullstelle der Geraden. Der Schnittwinkel mit der x-Achse ist |α|.
