Die Spiegelung am Kreis

zubereitet für SchülerInnen ab der 9. Klasse

Florian Borges

• Verlag: Books on Demand
• Jahr: 2015
• ISBN drucken: 9783734791864
• eBook-ISBN: 9783739252490
• Auflage: 2
• Thema: Matematica
• Thema: Geometria

Die Kreisspiegelung schlummert meist verborgen in der Schatzkiste der Mathematik - dabei ist sie bereits den Schülerinnen und Schülern der 9. Klasse zugänglich, sie benötigen nicht mehr als den Satz des Pythagoras zum Verständnis und finden jede Menge überraschender, faszinierender Eigenschaften dieser Abbildung, die weit mehr zu bieten hat als die üblichen Kongruenz- bzw. Ähnlichkeitsabbildungen der Schulmathematik. Für angehende und/oder geometrisch interessierte Lehrkräfte eignet sich dieses Schmankerl ebenso hervorragend wie für ältere Schüler in W-Seminaren oder ähnlichen studienvorbereitenden Veranstaltungen. Interaktives Arbeiten am Computer und eigenes Forschen zum Thema wird möglich durch die Verfügbarkeit der meisten Abbildungen als Geogebra-Datei, die beim Autor angefragt werden können und gerne zugeschickt werden. Ziel des Autors ist es, Schüler und Lehrkräfte mit seiner Faszination für die Inversion anzustecken, wer sich dem hingibt, merkt bald: es lohnt sich!

1. Einführung der Kreisspiegelung

In diesem Kapitel werden wir die Kreisspiegelung kennen- und hoffentlich auch gemeinsam schätzen lernen. Zu diesem Zweck wird sie als Abbildung zunächst durch eine geeignete, sehr einfache Vorschrift festgelegt. Gleich darauf werden wir uns überlegen, warum diese Zuordnung mit Recht eine „Spiegelung“ genannt wird und in welch enger Beziehung sie zur bekanntesten aller Spiegelungen, nämlich der an einer (geraden) Achse, steht.

Bei der Untersuchung der Bilder von Geraden und Kreisen stoßen wir auf verblüffende Ergebnisse, die uns von den bisher bekannten (linearen) Abbildungen her völlig unbekannt waren: Geraden werden meistens auf Kreise abgebildet, Kreise manchmal auch auf Geraden! Einigermaßen erholt von diesem Schock prüfen wir, ob es Fixpunktmengen oder Fixmengen bei dieser sogenannten „Inversion“ gibt. Einige Aufgaben sollen die frischen Erkenntnisse vertiefen, ehe eine letzte, unerwartete Eigenschaft dieser Abbildung behandelt wird: obwohl sie weder geraden-, längen- noch flächentreu ist, bleiben nämlich Winkel (bis auf den Drehsinn) erhalten! Der Abschnitt schließt mit einer kurzen Zusammenfassung der abbildungsgeometrischen Neuigkeiten.

1.1. Abbildungsvorschrift der Spiegelung am Kreis k_s((M_s;;r_s)):

(Abb.1)

Wegen der Eindeutigkeit der zugrundeliegenden, stets möglichen Konstruktion sieht man:

Zu jedem Punkt P beliebig außerhalb des Spiegelkreises k_s gibt es genau einen Bildpunkt P' innerhalb k_s\{M_s}mit folgenden Eigenschaften:

a) P' liegt auf [M_s P und

b) P' liegt auf [T₁T₂],wobei T₁ und T₂ die Berührpunkte der Tangenten durch P an k_s sind.

Zu P innerhalb k_s\{M_s} gilt die umgekehrte Abbildungsvorschrift entsprechend (Lot auf den Radius durch P schneidet k_s in T₁ und T₂, die dortigen Tangenten schneiden sich in P')

Definiert ist die Kreisspiegelung überall in der Ebene außer in M_s. Die Abbildung ordnet also jedem Punkt außerhalb k_s genau einen Punkt innerhalb k_s\{M_s} zu und umgekehrt! An der Abbildungsvorschrift erkennt man gleich: Die Kreisspiegelung ist selbstinvers. Fixpunkte der Kreisspiegelung sind genau die Punkte der Spiegelkreislinie (vgl. dazu auch 1.2.3. sowie Achsen- und Punktspiegelung).

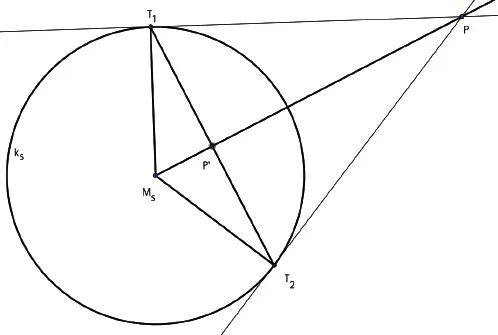
1.2. Eigenschaften der Kreisspiegelung

Zunächst wollen wir den Namen „Spiegelung“ rechtfertigen, ehe wir die Bilder von bestimmten Sorten von Geraden und Kreisen betrachten.

1.2.1. Grenzverhalten für große Spiegelkreis-Radien

Nach dem Kathetensatz (aus der Satzgruppe des Pythagoras, siehe Abb.1) gilt:

(für beliebiges P)

Im Grenzübergang "Spiegelkreisradius r_s gegen unendlich" wird die Kreisspiegelung zur bekannten Achsenspiegelung:

(Abb.2)

Anhand von Abb.2 wollen wir uns überlegen, wie sich das Bild P' eines Punktes P verändert, wenn man den Spiegelkreisradius immer größer werden läßt. Dabei halten wir den rechten Rand des Kreises fest und lassen stattdessen den Mittelpunkt M immer weiter nach links wandern. Der Schnittpunkt S der Halbgeraden [MP mit ks sowie der Punkt P bleiben so immer an der gleichen Stelle. Betrachten wir das Verhältnis der Längen der Strecken [PS] und [P'S]:

Weil der Term

für große r immer kleiner wird und schließlich immer weniger von Null abweicht, wird das Verhältnis der Streckenlängen immer weniger von 1 abweichen, d.h. die Kreisspiegelung unterscheidet sich immer weniger von der Achsenspiegelung.

Weiterhin kann man anschaulich sagen (und das ist eine sehr bemerkenswerte Feststellung):

Die Kreisspiegelung "klappt" alles außerhalb k_s (d.h. eine unendlich große Fläche!) nach innen (in eine endlich große Fläche!) und umgekehrt; bildet man endlich viele Punkte so ab, so wird die "Bildpunktdichte" beim "Hineinspiegeln" umso größer, je näher das Bild bei M_s liegt.

En...

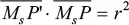
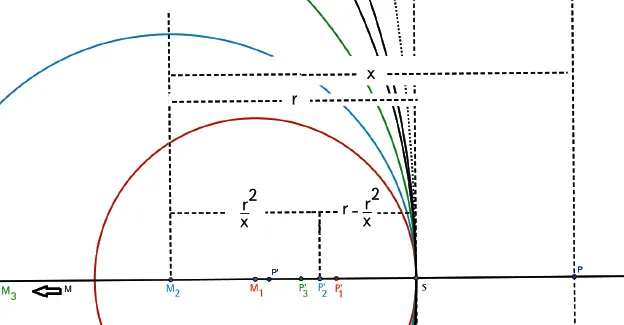
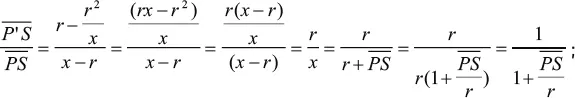
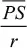
Inhaltsverzeichnis

• Inhaltsverzeichnis
• Vorbemerkung
• 0. Hilfreiche Voraussetzungen
• 1. Einführung der Kreisspiegelung
• 2. Beispiele für Spiegelei-Spielerei
• 3. Die Kreisspiegelung - eine alte Bekannte!
• 4. Die Funktionsgleichung der Kreisspiegelung
• 5. Die Spiegelbilder der Kegelschnitte
• 6. Weitere Verfahren zur Bildpunktkonstruktion
• 7. Mascheronische Konstruktionen
• 8. Ein mechanischer Kreisspiegler zum Selbstbauen
• 9. Die stereographische Projektion
• 10. Die Berühreigenschaften des Feuerbachkreises als Anwendung
• 11. Die „große Schwester“ der Kreisspiegelung – die Kugelinversion
• 12. Getriebe des Teufels – oder: Kann die Inversion tatsächlich Erdbeben verhindern?
• 13. Ergänzung: Der Sehnen - Tangenten - Satz Schlussbemerkung
• Schlussbemerkung
• Literaturhinweise
• Impressum