Jetzt lerne ich Stochastik für die Oberstufe

www.mathe-total.de

Marco Schuchmann

• Verlag: Books on Demand
• Jahr: 2012
• ISBN drucken: 9783844812534
• eBook-ISBN: 9783844826104
• Auflage: 3
• Thema: Mathematik
• Thema: Hochschulausbildung

In diesem Buch werden Anwendungen der Stochastik in der Oberstufe mit vielen Beispielen beschrieben. Die Beschreibungen orientieren sich an den Aufgaben- und Problemstellungen, wie sie in der Oberstufe an Gymnasien als auch an Fachoberschulen behandelt werden. Das Buch kann man auch zur Abiturvorbereitung verwenden, wenn man selbstständig noch mal den Stoff der Klassen 12 und 13 aufarbeiten möchte.Zum Inhalt des Buches gehören die Grundlagen der Kombinatorik, die Erstellung vonWahrscheinlichkeitsbäumen, die Berechnung des Erwartungswertes und der Varianz, die Berechnung von Kenngrößen von Stichproben, bedingte Wahrscheinlichkeiten und Kreuztabellen, das Bernoulli-Experiment und die Binomialverteilung, die Berechnung der Sigma-Umgebung, die Durchführung von Hypothesentests und Grundlagen zur Normalverteilung.Es wurden viele Erklärungen, wichtige Hinweise für bestimmte Aufgabentypen, Aufgabenbeispiele mit Lösungstipps und Grafiken eingefügt. Bei allen Beschreibungen wurde darauf geachtet, dass diese für Schülerinnen und Schüler möglichst verständlich sind. Weitere Aufgaben, Ergänzungen und Beispiele zum Buch sind auf der Seite www.mathe-total.de zu finden.

1 Grundlagen

1.1 Grundbegriffe

Alle möglichen Ereignisse eines Zufallsexperiments fassen wir in einer Ereignismenge Ω zusammen. Ereignisse sind Teilmengen von Ω. Umfasst das Ereignis nun ein Element von Ω, dann handelt es sich um ein Elementarereignis.

Beispiel:

Bei einem Würfel mit sechs Seiten wäre Ω={1, 2, 3, 4, 5, 6}.

Ein mögliches Ereignis A ist, dass man eine gerade Zahl würfelt:

A={2, 4, 6}

Ein Elementarereignis wäre B={6}, also das Ereignis, dass eine 6 gewürfelt wird.

Laplace-Experiment:

Man geht davon aus, dass es nur endlich viele Elementarereignisse gibt: |Ω| = n.

Jedes Elementarereignis E soll mit derselben Wahrscheinlichkeit auftreten

.

Somit gilt für ein Ereignis

.

Beispiel „fairer“ Würfel:

Hier gibt es 6 mögliche Elementarereignisse, wobei jedes (deshalb „fairer Würfel“) mit der gleichen Wahrscheinlichkeit auftritt. Beispielsweise gilt dann:

Es gilt folgendes Gesetz für zwei Ereignisse A und B:

P(A∪B) = P(A) + P(B) − P(A∩B)

Beispiel:

In einer Urne sind 20 Kugeln mit den Ziffern von 1, 2, …, 20 beschriftet. Es wird zufällig eine Kugel gezogen.

Wir betrachten folgende Ereignisse:

A: Es wird eine Kugel mit einer Ziffer gezogen, die durch 9 teilbar ist.

B: Es wird eine Kugel mit einer Ziffer gezogen, die durch 6 teilbar ist.

A = {9, 18}

B = {6, 12, 18}

A∩B = {18}

Das ist das gleiche wie P(A ∪B) = P({6, 9, 12, 18})

Weiterhin gilt:

Beispiel:

A sei das Ereignis, dass keine 6 geworfen wird: A = {1, 2, 3, 4, 5}

Damit ergibt sich das Komplement von A (dies sind alle Elemente von Ω = {1, 2, 3, 4, 5, 6}, die nicht in A liegen):

Somit gilt:

Bemerkung:

Diese Formel wir bei der Berechnung von Wahrscheinlichkeiten bei der Binomialverteilung später oft verwendet. Man kann sie auch einsetzen, wenn die Berechnung der Wahrscheinlichkeit für P(A) aufwändig wäre und man P(

) einfach berechnen kann.

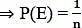
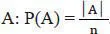
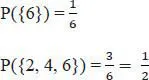
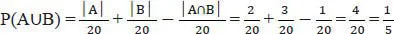
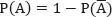
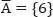
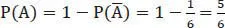
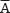
1.2 Wahrscheinlichkeitsbaum

Eine Urne enthält 10 blaue (b), 6 rote (r) und 4 gelbe (g) Kugeln. Es wird 2-mal mit Zurücklegen eine Kugel gezogen.

Hier sind folgende Elementarereignisse denkbar: {(b, b), (b, r), (b, g), (r, b), (r, r), (r, g), (g, b), (g, r), (g, g)}

Dies sind 3² = 9 Elementarereignisse. Würde man dreimal ziehen, so ergäben sich 3³ = 27 Elementarereignisse.

Man kann dieses Zufallsexperiment mit einem Baum darstellen (wie allgemein bei Experimenten, die wiederholt ausgeführt werden).

Die Wahrscheinlichkeit, dass beide Kugeln blau sind, ergibt sich durch

Die Wahrscheinlichkeit, dass eine Kugel (d.h. genau eine) blau ist wäre:

Wie sieht es aus, wenn ohne Zurücklegen gezogen wird?

Hier würde sich nach jedem Zug die Wahrscheinlichkeiten ändern, da die jeweils gezogene Kugel fehlt. Wir zeichnen für diesen Fall einen Baum mit den entsprechenden Wahrscheinlichkeiten.

Hier wäre beispielsweise

Ein weiteres Beispiel für die Verwendung eines Baumes:

Es wird 3-mal gewürfelt. Wie groß ist die Wahrscheinlichkeit dabei mindestens eine 6 zu würfeln (Ereignis A)?

1. Möglichkeit:

Die Wahrscheinlichkeit beträgt:

Sobald im Baumdiagramm eine 6 vorkommt, kann der Ast beendet werden (das wäre das selbe, wie bei einem Spiel, bei dem ein Spieler 3-mal würfelt und gewinnt, sobal...

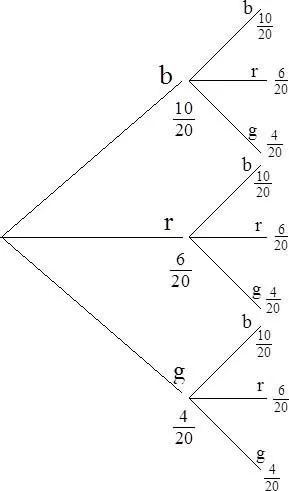
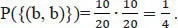
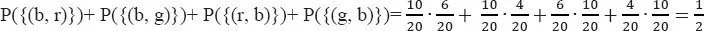
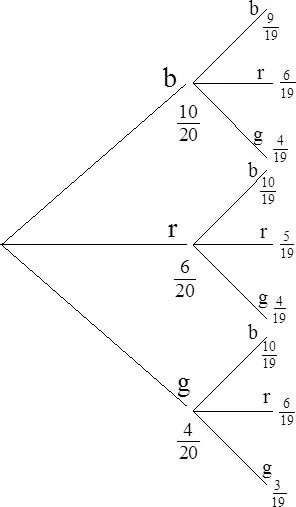
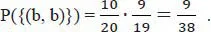
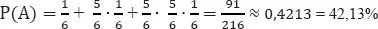
Inhaltsverzeichnis

• TITELSEITE
• VORWORT
• INHALTSVERZEICHNIS
• 1. GRUNDLAGEN
• 2. KOMBINATORIK
• 3. ERWARTUNGSWERT UND VARIANZ
• 4. STICHPROBEN UND DEREN KENNGRÖßEN
• 5. BEDINGTE WAHRSCHEINLICHKEIT, KREUZTABELLEN UND UNABHÄNGIGKEIT
• 6. DIE BINOMIALVERTEILUNG
• 7. DIE TSCHEBYSCHEFF-UNGLEICHUNG
• 8. AUFGABEN ZUR STOCHASTIK
• 9. ANHANG
• IMPRESSUM