Warum sind manche Stoffe fest, andere aber flüssig? Schwimmt ein Schiff auch in der Badewanne? Wie kalt ist es im Weltraum? Was uns beschäftigt und gleichzeitig fasziniert, sind nicht die alltäglichen Dinge. Physik erweist sich als gute Basis unsere von Naturwissenschaft und Technik geprägte Welt besser zu verstehen.Pumping-Physics regt mit interessanten, oft spannenden und vor allem auch für Laien verständlichen Themen dazu an, sich mit diesen Fragen zu beschäftigen. Die Beispiele werden in Form einer klar umrissenen Frage und Beantwortung mittels vorgegebener Auswahlmöglichkeiten präsentiert.Anschauliche Fragestellungen führen Schritt für Schritt auch durch schwieriges Terrain und vermitteln die Fähigkeiten, die Antworten darauf selbst nachvollziehen zu können.Mit Kenntnis und Freude an der Sache geschrieben und mit über 350 zum Teil farbigen Abbildungen pfiffig illustriert wird die Lektüre dennoch nicht zur Anstrengung. Physik kann auch Spaß machen.Anschaulich und treffend zugleich, leicht geschrieben und durchweg illustriert, dabei immer exzellente Physik. Pumping-Physics macht es vor.Brian Clegg, Science-Autor.
Häufig gestellte Fragen
Ja, du kannst dein Abo jederzeit über den Tab Abo in deinen Kontoeinstellungen auf der Perlego-Website kündigen. Dein Abo bleibt bis zum Ende deines aktuellen Abrechnungszeitraums aktiv. Erfahre, wie du dein Abo kündigen kannst.
Derzeit stehen all unsere auf mobile Endgeräte reagierenden ePub-Bücher zum Download über die App zur Verfügung. Die meisten unserer PDFs stehen ebenfalls zum Download bereit; wir arbeiten daran, auch die übrigen PDFs zum Download anzubieten, bei denen dies aktuell noch nicht möglich ist. Weitere Informationen hier.
Perlego bietet zwei Pläne an: Elementar and Erweitert
Elementar ist ideal für Lernende und Interessierte, die gerne eine Vielzahl von Themen erkunden. Greife auf die Elementar-Bibliothek mit über 800.000 professionellen Titeln und Bestsellern aus den Bereichen Wirtschaft, Persönlichkeitsentwicklung und Geisteswissenschaften zu. Mit unbegrenzter Lesezeit und Standard-Vorlesefunktion.
Erweitert: Perfekt für Fortgeschrittene Studenten und Akademiker, die uneingeschränkten Zugriff benötigen. Schalte über 1,4 Mio. Bücher in Hunderten von Fachgebieten frei. Der Erweitert-Plan enthält außerdem fortgeschrittene Funktionen wie Premium Read Aloud und Research Assistant.
Beide Pläne können monatlich, alle 4 Monate oder jährlich abgerechnet werden.
Wir sind ein Online-Abodienst für Lehrbücher, bei dem du für weniger als den Preis eines einzelnen Buches pro Monat Zugang zu einer ganzen Online-Bibliothek erhältst. Mit über 1 Million Büchern zu über 1.000 verschiedenen Themen haben wir bestimmt alles, was du brauchst! Weitere Informationen hier.
Achte auf das Symbol zum Vorlesen in deinem nächsten Buch, um zu sehen, ob du es dir auch anhören kannst. Bei diesem Tool wird dir Text laut vorgelesen, wobei der Text beim Vorlesen auch grafisch hervorgehoben wird. Du kannst das Vorlesen jederzeit anhalten, beschleunigen und verlangsamen. Weitere Informationen hier.
Ja! Du kannst die Perlego-App sowohl auf iOS- als auch auf Android-Geräten verwenden, um jederzeit und überall zu lesen – sogar offline. Perfekt für den Weg zur Arbeit oder wenn du unterwegs bist. Bitte beachte, dass wir keine Geräte unterstützen können, die mit iOS 13 oder Android 7 oder früheren Versionen laufen. Lerne mehr über die Nutzung der App.
Ja, du hast Zugang zu Pumping-Physics von Ottmar Kögel im PDF- und/oder ePub-Format sowie zu anderen beliebten Büchern aus Naturwissenschaften & Physik. Aus unserem Katalog stehen dir über 1 Million Bücher zur Verfügung.
Auch die Physik des 21. Jahrhunderts beginnt mit dem Studium der Mechanik. So erschließt sich am einfachsten die Bedeutung vieler physikalischer Grundprinzipien wie die Erhaltungsätze oder das Wechselwirkungsprinzip.
Seit Galileo Galilei nehmen das Experiment und die Messung von Größen eine zentrale Stellung ein. Der Vorteil des Experimentierens gegenüber der reinen Beobachtung liegt darin, dass im Experiment die Versuchsbedingungen verändert und so der Einfluss einer Größe auf eine andere untersucht werden kann. Dabei verfolgt der Physiker die Vorgänge immer auch messend. Die Resultate werden miteinander in Zusammenhang gebracht, um die Abhängigkeit der Größen zu erkennen oder sogar ein physikalisches Gesetz zu erhalten.
Das sich daraus entwickelnde Wechselspiel von Modellbildung und experimenteller Untersuchung ist bis heute kennzeichnend für die physikalische Forschung.
Neben der grundlegenden Vorgehensweise zur Gewinnung neuer Erkenntnisse kamen auch typische Methoden der Physik ursprünglich aus der Mechanik.
Ein wichtiges Ziel der Mechanik ist es, die Bewegung von Körpern unter dem Einfluss von Kräften zu beschreiben. Dazu werden Bewegungsgleichungen aufgestellt, deren formelmäßige Lösung dann z. B. die gewünschte Bahnkurve des Körpers ergibt.
Daher stehen die grundsätzlichen Bewegungsgrößen am Anfang.
Die Kinematik behandelt die Gesetzmäßigkeiten, die den Bewegungsabläufen zugrunde liegen. Die bei der Bewegung auftretenden Kräfte bleiben unberücksichtigt. Man unterscheidet zwei Arten von Bewegung: geradlinige Bewegung (Translation) und Drehbewegung (Rotation).
Werden auch die auftretenden Kräfte und Massen mit einbezogen, werden aus reinen Bewegungsabläufen dynamische Prozesse. Das Konzept der Kraft ist fundamental in Physik und Technik, um beispielsweise die Bewegung eines Körpers vorherzusagen.
Die berühmten Newtonschen Gesetze dürfen bei diesem Einstieg natürlich nicht fehlen.
Größen und Einheiten
Eine Messung könnte ein Resultat wie das obige liefern: Eine Strecke von s = 20 m. Sie liefert eine physikalische Größe, die aus einem Zahlenwert und einer Einheit besteht. Die Stoppuhr gibt die benötigte Zeit von t ≈ 2 s.
Größen (Formelzeichen) wie „s“ und „t“ werden kursiv, die Symbole für Einheiten wie „m“ für Meter oder „s“ für Sekunde immer in Normalschrift dargestellt.
Präfixe für SI-Einheiten
Faktor
Präfix
Zeichen
1012
Tera-
T
109
Giga-
G
106
Mega
M
103
Kilo-
K
102
Hekto
H
101
Deka-
da
10-1
Dezi-
d
10-2
Zenti-
c
10-3
Milli-
m
10-6
Mikro-
μ
10-9
Nano-
n
10-12
Piko-
P
10-15
Femto-
f
Eine Zusammenstellung wichtiger (SI) Einheiten findet sich im Anhang.
Auch für sehr große oder sehr kleine Zahlenwerte gibt es kürzere Schreibweisen. Entweder in der sogenannten wissenschaftlichen Notation mit 10er-Potenzen oder mit bestimmten Präfixen, die jeweils einer Potenz entsprechen. Die Strecke 1250 m lässt sich somit abkürzen zu: 1,25 103 m bzw. 1,25 km. Insbesondere für die Mechanik wichtige Basisgrößen sind
Länge
Vor gut 100 Jahren wurde die Längeneinheit Meter (m) über zwei Kerben in einem Metallstab festgelegt. Von diesem in Paris aufbewahrten Original wurden exakte Kopien an alle Normungsbehörden weltweit verschickt. Heute geht die Einheit Meter auf eine Naturkonstante zurück, nämlich die Lichtgeschwindigkeit:
Ein Meter ist die Entfernung, die das Licht im Vakuum in
Sekunden zurücklegt.
Die Bestimmung der Länge wird letztlich auf eine hochpräzise Zeitmessung zurückgeführt.
Zeit
Die Zeitmessung basiert auf einem periodischen Vorgang. Naheliegend wurden früher Stunde, Minute und Sekunde auf die tägliche Rotation der Erde zurückgeführt. Im 17. Jh. aufkommende Uhren nutzten die regelmäßigen Schwingungen von Pendeln oder Federn.
Heute definiert man die Zeit ebenfalls über eine Naturkonstante:
Taktgebende Schwingung zur Definition der Zeiteinheit Sekunde (s) ist eine bestimmte Oszillation des Caesiumatoms. Diese extrem schnelle Schwingung ermöglicht die von Atomuhren bekannte Ganggenauigkeit.
Masse
Noch wird die Masseneinheit Kilogramm (kg) über einen Zylinder aus einer Platin-Iridium-Legierung festgelegt, der sich ebenfalls in Paris befindet und von dem es weltweit Kopien gibt. Für Messungen auf atomarer Skala verwendet man die atomare Masseneinheit u, die anhand des Kohlenstoff-12-Atom definiert ist. Aktuell wird im aus Deutschland koordinierten Avogadro-Projekt eine Neudefinition des Kilogramms über das „Zählen“ von Atomen in einem Silizium-Einkristall angestrebt.
Besser messen
Zu den ganz grundlegenden Messungen gehört die Bestimmung von Zeitpunkten oder Zeitintervallen. Dazu nutzt man einfache, mechanische Stoppuhren, die man über Druckknöpfe bedient. Manche haben eine Digitalanzeige. Für eine höhere Präzision gibt es auch elektronisches Zeitmess-Equipment. Alle Messungen jedoch hängen, neben der Ganggenauigkeit der verwendeten Uhren, vom exakten Starten bzw. Stoppen der Zeitmessung ab. Das Erfassen kurzer Zeitintervalle mit einer Stoppuhr ist problematisch, da das Drücken der Start-Stopp-Knöpfe große Unsicherheiten mit sich bringt.
Wie kann man diese systembedingten Unzulänglichkeiten abmindern oder weitgehend ausschließen?
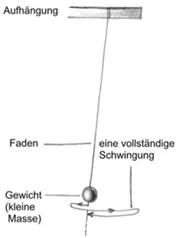
Wiederholen der gleichen Messung und bilden des Mittelwertes
Es bleibt nur eines: Den Umgang mit der Stoppuhr trainieren
Bei periodischen Vorgängen kann man die Messung über einen längeren Zeitraum durchführen und das Ergebnis durch die Anzahl der Perioden teilen.
Antwort
Die Antworten a) und c) sind richtig Beide Wege sind das Standard-Verfahren zur Erhöhung der Messgenauigkeit. Das Wiederholen ein und derselben Messung und die Bildung des Mittelwertes ist über die sogenannte Fehlerrechnung sogar mathematisch exakt definiert. Die Anzahl ...
