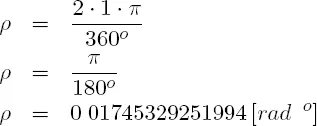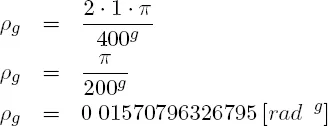Geoinformatik

Von den Grundlagen zum Fachwissen

Markus Penzkofer

• Verlag: Books on Demand
• Jahr: 2017
• ISBN drucken: 9783741251405
• eBook-ISBN: 9783743170988
• Auflage: 2
• Thema: Ciencias físicas
• Thema: Geografía

In diesem Manuskript sollen einige theoretische Hintergründe und Zusammenhänge der Geoinformatik zusammengestellt werden. Auch die wichtigsten Formeln aus Mathematik, Niederer Geodäsie, Höherer Geodäsie und Kartographie sollen kurz vorgestellt werden. Neben diesen Fächern bildet natürlich die Informatik einen wesentlichen Bestandteil von Geoinformationssystemen. Anschließend werden alle Grundlagen zu einem kurzen Überblick über die Geoinformatik vereint, wobei insbesondere die Modellierungen, Erweiterungen, Spezialisierungen und Analysen der Geoinformatik gezeigt werden. Die vom Autor erstellte Open Source GIS-Anwendung MensorGIS setzt die besprochene Thematik in Quellcode und Funktionalität um. In einem abschließenden Kapitel wird aufgezeigt, wo sich dort die Grundlagen am besten erkennen lassen. Als Zusatz wird die in allen Fachgebieten des Vermessungswesens wichtige Ausgleichungsrechnung mit Beispielen vorgestellt.A Geoinformatik - von der Theorie zur Anwendung1 Einführung2 Überblick über die Grundlagen der Geoinformatik3 Grundlagen der Mathematik4 Grundlegende Berechnungen der Niederen Geodäsie5 Grundlegende Berechnungen der Höheren Geodäsie6 Grundlagen der Kartographie und Photogrammetrie7 Grundlagen der Informatik8 Geoinformatik9 Praktische Anwendung in MensorGISB Statistik und Ausgleichungsrechnung1 Einführung2 Grundlagen der Statistik3 Grundlagen der Matrizenrechnung4 Ausgleichungsrechnung5 Anwendung der AusgleichungsrechnungMit umfangreichem Anhang und Index.Das Buch sollte von Studenten gelesen werden, die in die Fachvorlesungen mit Schwerpunkt Geoinformatik einsteigen. Auch Quereinsteigern zu empfehlen, die sich für die geodätischen Hintergründe der Geoinformationssysteme interessieren.

Kapitel 1

Einführung

1.1 Anwendungsfelder der Geoinformatik

Die Geoinformatik besitzt viele unterschiedliche Anwendungsbereiche, die heutzutage auch der Öffentlichkeit bekannt sind. Reine Expertensysteme sind nun die Ausnahme, wobei hinter jeder Nutzeroberfläche selbstverständlich nach wie vor ein Kern steckt, der von einem fachlichen Administrator bedient werden muss. Üblicherweise werden die Anwendungsbereiche von GIS-Anwendungen wie folgt eingeteilt:

• Fach-Informationssysteme, z.B. Grunddaten-Erfasser, Umwelt-Informationssysteme, Energie- u. Wasser-Dienstleister, Flottenmanagement
• Öffentliche Informationssysteme, z.B. Routing (Navigationssystem), Google Earth, Location Based Services, Geodatenportale

1.2 Zeilsetzung dieses Skripts

In diesem Manuskript sollen einige theoretische Hintergründe und Zusammenhänge der Geoinformatik zusammengestellt werden. Auch die im Kontext Geoinformatik wichtigsten Formeln aus Mathematik, Niederer Geodäsie, Höherer Geodäsie und Kartographie sollen kurz vorgestellt werden. Neben diesen Fächern bildet natürlich die Informatik einen wesentlichen Bestandteil der GIS-Anwendungen. Anschließend werden alle Grundlagen zu einem kurzen Überblick über die Geoinformatik vereint, wobei insbesondere die Modellierungen, Erweiterungen, Spezialisierungen und Analysen der Geoinformatik gezeigt werden. In einem abschließenden Kapitel werden Funktionalität und Quellcode der Open-Source GIS-Anwendung MensorGIS dahingehend diskutiert, wo sich dort die Grundlagen am besten erkennen lassen. Ziel dieses GIS-Projekts ist nicht seine operative Verwendung, sondern die beispielhafte Umsetzung von Algorithmen. MensorGIS ist frei verfügbar unter: https://sourceforge.net/projects/mensorgis/.

Dieses Skriptum kann für jeden einzelnen Fachbereich nur die grundlegenden Thematiken ansprechen; falls das eine oder andere vermisst wird, sollte in der entsprechenden Fachliteratur nachgeschlagen werden (siehe auch Literaturverzeichnis im Anhang A). Das Buch sollte von Studenten, ggf. auch von Quereinsteigern, gelesen werden, die in Fachvorlesungen mit Schwerpunkt Geoinformatik einsteigen.

Das nächste Kapitel gibt eine Übersicht über die einzelnen Disziplinen, die bei der Konzipierung, Programmierung und Nutzung eines GIS notwendig sind. Dabei wird u.a. auch auf die bei der Implementierung zu beachtenden Sachverhalte verwiesen.

Wichtige Begriffe sind in Fettdruck, zusätzliche Begriffe und Kapitelverweise in kursiver Schrift angegeben.

Kapitel 2

Überblick über die Grundlagen der Geoinformatik

Wenn über GIS-Anwendungen gesprochen wird, werden meistens Grundlagen aus Mathematik, Landesvermessung und Informatik genannt. Wenn man jedoch an die Herkunft der GIS-Daten denkt, gehören sowohl einige der Messverfahren der Niederen Geodäsie vor dem GPS-Zeitalter als auch die Photogrammetrische Herstellung von Orthophotos und Geländemodellen dazu. Daneben werden einige wichtige Methoden der Kartographie auch in GIS-Anwendungen benötigt. Das Vermessungswesen bringt das traditionelle Wissen ein, die Informatik stellt die Grundlagen zur Einführung neuer Techniken in die Informationsverarbeitung von Geodaten zur Verfügung.

2.1 Die Mathematik

Die Mathematik bildet die Grundlage für viele Ingenieurwissenschaften, aber auch für die theoretischen und praktischen Anwendungen der Informatik. Im Hinblick auf die Geoinformatik fließt sie beginnend bei der Niederen und Höheren Geodäsie über Kartographie und Photogrammetrie schließlich auch in die Informatik und Geoinformatik ein.

Die grundlegenden geodätischen Anwendungen betreffen v.a. die Trigonometrie, Geometrie und Matrizenrechnung. Kartographie und Photogrammetrie benötigen dieselben Grundlagen, daneben noch Interpolationsverfahren. In der Informatik spielen bei der Programmierung die Zahlendarstellung und die Boolsche Logik eine Rolle. Eine spezielle GIS-Analyse basiert auf der Graphentheorie als Teilgebiet der mathematischen Topologie.

2.2 Die Niedere Geodäsie

Die Niedere Geodäsie umfasst alle Berechnungen, die unter Annahme einer ebenen Bezugsfläche durchgeführt werden können. Dazu wird entweder ein lokales ebenes Koordinatensystem verwendet oder mit Koordinaten aus einer Projektion gerechnet. Höhenwerte werden klassischerweise getrennt von Grundrissdaten gemessen (Ausnahme GPS).

Aus der Niederen Geodäsie stammen die meisten praktischen Messdaten, wenn man auch die Messung von GPS heutzutage als „normalen“ Vermessungsalltag betrachtet.

2.3 Die Höhere Geodäsie

Die Höhere Geodäsie basiert auf der Festlegung einer Bezugsfläche, die im Gegensatz zur Niederen Geodäsie gekrümmt ist, d.h. in früheren Zeiten eine Kugel, in der jüngeren Geschichte ein Ellipsoid oder Geoid zur Repräsentation der Erde. Die Höhere Geodäsie legt landes- oder weltweite Bezugssysteme fest. Außerdem beschäftigt sie sich mit der Messung und Definition des Erdschwerefeldes (in Bezug auf GIS nicht weiter zu verfolgen). Eine Methode, die sowohl in der Niederen und Höheren Geodäsie als auch in der Photogrammetrie verwendet wird, ist die Ausgleichungsrechnung (siehe auch zweiten Teil dieses Buchs).

2.4 Kartographie und Photogrammetrie

Mittels Methoden der Kartographie kann eine systematische Darstellung (Kartierung) von gemessenen und berechneten Objekten erfolgen. Zwei Teilgebiete der Kartographie sind für die Geoinformatik wesentlich: Zum einen die mathematischen Berechnungsverfahren zur Abbildung dieser Objekte in die Ebene (Kartenprojektion), zum anderen die graphische Aufbereitung und Ausgestaltung der Objekte in Geometrie und Erscheinungsform (z.B. Generalisierung, Farbgebung, Schraffur, Thematische Darstellung).

Die Photogrammetrie ermittelt aus zweidimensionalen Bilddaten dreidimensionale Koordinaten. Auf diesem Weg können ebenfalls Daten gewonnen werden, die zur Kartierung und/oder als Eingabe in ein GIS verwendet werden. Wie die Niedere Geodäsie ist die Photogrammetrie somit ein Datenlieferant für GIS-Anwendungen, die Kartographie kann diese als auch die terrestrisch ermittelten Daten verwenden.

2.5 Die Informatik

Die Informatik stellt heutzutage Rechen- und Datenhaltungswerkzeuge zur Verfügung. Von der zeilenweisen Eingabe in Computeralgebra-Systemen bis hin zur Erstellung eigenständiger Programme mit graphischer Oberfläche reichen die Möglichkeiten der Informatik, um Berechnungen zu automatisieren.

Eigenständige Programme bieten i.d.R. zusätzlich den Import, Export sowie die dauerhafte Speicherung der Daten in einer Datenbank an. Dies setzt eine durchdachte Datenmodellierung voraus. Wesentlicher Bestandteil heutiger GIS-Anwendungen ist auch eine Möglichkeit zur graphischen Darstellung der Daten. Hier spielt die Computergraphik eine bedeutende Rolle. Im Zeitalter des Internets finden Verteilte Systeme zunehmende Verbreitung.

2.6 Die Geoinformatik

Die Geoinformatik vereint vieles aus den bisher genannten Grundlagen. Insbesondere die Art der Datenhaltung und Datenmodellierung sowie die Visualisierungsund Analysemöglichkeiten zeichnen GIS-Anwendungen aus. Dabei gibt es gegenüber der Informatik und auch den anderen klassischen Fachrichtungen viele Erweiterungen und Spezialisierungen. Davon soll im Kapitel über Geoinformatik die Rede sein.

Kapitel 3

Grundlagen aus der Mathematik

Die Mathematik ist natürlich viel zu umfangreich, um hier vollständig dargestellt zu werden. Im Folgenden sollen nur die für die Niedere Geodäsie, Kartographie und Geoinformatik wesentlichen Teilgebiete herausgenommen werden.

3.1 Trigonometrie

Die Trigonometrischen Funktionen Sinus, Cosinus, Tangens, deren Inverse und weitere trigonometrische Funktionen treten sowohl in der Geodäsie (z.B. bei Transformationen) als auch in der Kartographie (z.B. bei Projektionen) häufig auf.

Bei der Programmierung ist zu beachten, daß die meisten Programmiersprachen Funktionsargumente in Radiant erwarten. Radiant ist die Angabe in Vielfachen von π und wird in Formeln als rad geschrieben.

3.1.1 Das Bogenmaß

Das Bogenmaß ist die Länge des Bogens, der zwischen den Schenkeln des Mittelpunktswinkels im Einheitskreis (Radius = 1) liegt.

Der Umrechnungsfaktor zwischen Gradmaß (Altgrad) und Bogenmaß beträgt:

Für Neugrad (Gon) gilt folgender Umrechnungsfaktor:

Diese Erwähnung klingt banal, der falsche oder vergessene Umrechnungsfaktor führt jedoch in längeren Berechnungen (Programmen) oft zu ärgerlichen Ergebnissen.

3.1.2 Das Rechtwinklige Dreieck

Formeln zur Auflösung des Rechtwinkligen Dreiecks treten in der Geodäsie sehr häufig auf. Die dem Rechten Winkel gegenüberliegende Seite bezeichnet man als Hypotenuse, die beiden anderen Seiten als Katheten. Deshalb hier die Definitionen der grundlegenden Trigonometrischen Funktionen im Rechtwinkligen Dreieck als Merkregeln:

• Sinus = Gegenkathete zu Hypotenuse
• Cosinus = Ankathete zu Hypotenuse
• Tangens = Gegenkathete zu Ankathete

Weitere mathematische Zusammenhänge wie z.B. trigonometrische Identitäten entn...

Inhaltsverzeichnis

• Hinweise
• Inhaltsverzeichnis
• 1 Einführung
• 2 Überblick über die Grundlagen der Geoinformatik
• 3 Grundlagen aus der Mathematik
• 4 Grundlegende Berechnungen der Niederen Geodäsie
• 5 Grundlegende Berechnungen der Höheren Geodäsie
• 6 Grundlagen der Kartographie und der Photogrammetrie
• 7 Grundlagen der Informatik
• 8 Geoinformatik
• 9 Praktische Anwendung in MensorGIS
• 10 Anhänge
• Impressum