Gewußt wie: Praxisleitfaden Seriation und Korrespondenzanalyse in der Archäologie

Frank Siegmund

• Verlag: Books on Demand
• Jahr: 2015
• ISBN drucken: 9783738654080
• eBook-ISBN: 9783739298016
• Auflage: 1
• Thema: Storia
• Thema: Storia mondiale

Seriation und Korrespondenzanalyse (CA) sind statistische Verfahren, die in der Archäologie häufig angewendet werden. Die CA dient vor allem dazu, die Kombination von Objekten (Typen) in zahlreichen Fundkomplexen wie z. B. Gräbern, Horten oder Siedlungsgruben zu analysieren, um deren relative zeitliche Abfolge aufzudecken. Das Buch führt in die Methode ein und bietet vor allem auf Basis der freien Software PAST eine praktische Einführung mit konkreten Übungsbeispielen. Der Text ist zum Selbststudium gedacht. Nach Durcharbeiten des Leitfadens und der Übungen ist der Leser in der Lage, selbständig eigene Analysen durchzuführen und auszuwerten. Der Praxisleitfaden ist von einem Archäologen für Archäologen geschrieben und mit Studierenden der Archäologie getestet, doch die Methode ist auch für andere Wissensbereiche wie etwa die Sozialwissenschaften oder Biologie und Ökologie relevant. Grundlage der praktischen Übungen ist die freie Software PAST, die für Rechner unter MS-Windows sowie MACs verfügbar ist.

1 Zielsetzung

Seriation und Korrespondenzanalyse (zu den Begriffen siehe Kap. 5) sind statistische Methoden, die oft auf archäologisches Material angewendet werden, vor allem bei einer chronologischen Fragestellung. Der Praxisleitfaden gibt Anfängern eine kurze Einführung in das Verfahren; dazu wird – soweit nötig – die statistische Theorie skizziert und vor allem eine praktische Einführung geboten. Für die hier vorgestellten Übungen und die eigene Praxis braucht es lediglich einen gewöhnlichen Computer, Zugang zum Internet, diesen Leitfaden und etwas Zeit und Energie, um den folgenden Text inklusive der praktischen Übungen gründlich durchzuarbeiten. Nach etwa acht Stunden konzentrierten Selbststudiums ist man kein Anfänger mehr, sondern in der Lage, die einschlägigen Publikationen besser zu verstehen und vor allem auch selbständig eigene Projekte mit “echten” Daten und Fragestellungen durchzuführen.

2 Einleitung

Korrespondenzanalyse – im Folgenden nach der englischen Bezeichnung correspondence analysis als CA abgekürzt – ist eine gut begründete multivariate Methode, mit der für die Zeilen und Spalten einer Tabelle eine optimale Reihenfolge gefunden werden kann, wenn die Daten dem unimodalen Modell folgen. Was bedeutet dieser Satz? Der Begriff “multivariat” meint statistische Verfahren, die viele Variablen gleichzeitig berücksichtigen – im Gegensatz zu Verfahren, die nur eine Variable untersuchen (univariat) oder den Zusammenhang zwischen zwei Variablen (bivariat), wie z. B. eine Korrelations- und Regressionsrechnung über den Zusammenhang zwischen Körperhöhe und -gewicht.

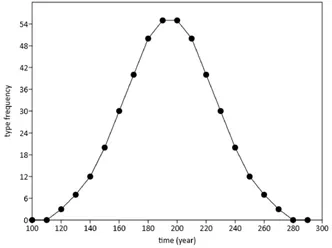
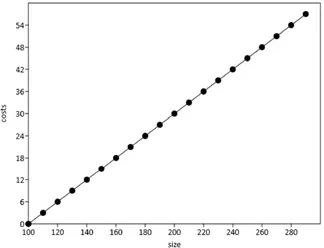
Der Begriff “unimodal” bezeichnet Phänomene, bei denen die Werte entlang einer Achse ein Maximum aufweisen und vorher ebenso wie nachher deutlich niedriger ausfallen oder Null betragen. Ein schönes Beispiel für eine unimodale Datenreihe ist die Glockenkurve (Abb. 1). Der Begriff unimodales Modell steht im Kontrast zu einem eher linearen Verhalten (“je mehr von A, desto mehr von B”) von Phänomenen (Abb. 2). Um diesen wichtigen Gegensatz anschaulich zu erklären, wählen wir aus dem Alltag bekannte Beispiele: Die Beziehung zwischen Körperhöhe und Körpergewicht bei Menschen ist tendenziell linear, ebenso die zwischen dem Gewicht eines Autos und seiner Geschwindigkeit einerseits und seinem Benzinverbrauch andererseits. Generell sind größere Menschen auch schwerer, kleinere Menschen auch leichter. Je schwerer ein Fahrzeug ist und je schneller es fährt, desto mehr Benzin verbraucht es. Gewiss handelt es sich bei diesen Beispielen nicht um einfache 1:1 Beziehungen, aber für die nähere Untersuchung solcher Phänomene wählt man lineare Verfahren. Ein gutes Alltags-Beispiel für ein unimodales Phänomen ist die übliche Beziehung zwischen dem Körpergewicht von Menschen und ihrem Lebensalter: Neugeborene sind noch vergleichsweise leicht und werden mit zunehmendem Alter schwerer; viele Menschen weisen ein Gewichtsmaximum irgendwann während ihres Erwachsenenlebens auf und sind im hohen Alter wieder etwas leichter.

Abb. 1. Unimodales Modell. Eine glockenförmige Kurve als Ideal für die Häufigkeitsverteilung eines archäologischen Phänomens entlang der Zeitachse. Zu Beginn wird ein neuer Typ gerade erst eingeführt, seine Häufigkeit steigt von Null auf gering. Danach wird er häufiger, ist modern, nach einem Maximum lässt seine Beliebtheit wieder nach bis hin zum völligen Verschwinden.

Abb. 2. Lineares Modell. Idealbild einer linearen Beziehung: Je mehr die eine Größe wächst, desto mehr wächst auch die andere Größe.

Die noch kurze Geschichte der Speichermedien für Computer ist ein anderes Beispiel für unimodale Modelle, und dieses Beispiel ist bereits sehr nah an den archäologischen Anwendungen der Korrespondenzanalyse. Mechanische Lösungen zur Informationsspeicherung wie etwa Lochstreifen und Lochkarten wurden in den 1960er Jahren allmählich durch die Speicherung auf großen rotierenden Magnetplatten abgelöst. Nach einigen Jahren der dominanten Verwendung von sog. Winchester-Laufwerken wurden diese in den 1980er Jahren sukzessive abgelöst durch 8-Zoll Floppy-Disks, dann 5¼-Zoll Floppy-Disks, dann 3½-Zoll Disketten und später durch wiederbeschreibbare CDs bis hin zu den aktuellen USB-Sticks (CHRISTENSEN 1997). Diese von vielen Zeitgenossen zumindest in Teilen erlebte Geschichte ähnelt den Vorstellungen in der Archäologie über Artefakte und Zeit: Ein spezieller Gegenstand – oft als “Typ” bezeichnet – ist noch nicht erfunden, seine Häufigkeit in der Welt beträgt Null. Nach seiner Erfindung und Einführung erscheint er zunächst in geringen Häufigkeiten in der Welt, sobald er sich durchgesetzt hat und “modern” wird, tritt er häufig auf. Später treten neue Objekte auf, die seine Stelle übernehmen und der von uns beobachtete Typ wird wieder seltener bis hin zu seinem völligen Verschwinden, d. h. seine Häufigkeit geht auf Null zurück (Abb. 1). Für die Analyse derartiger Phänomene ist die CA das Verfahren der Wahl. Dabei ist es nicht erforderlich, dass wie bei einer Glockenkurve – Statistiker sprechen hier häufig von einer “Normalverteilung” – eine exakte Symmetrie des Bildes gegeben ist. Der Begriff unimodal erwartet nur, dass es ein Maximum irgendwo innerhalb der untersuchten Reihe gibt, während an beiden Enden Minima beobachtet werden. Abweichungen vom Idealbild einer Glockenkurve sind erlaubt und beeinflussen das Ergebnis einer CA nicht schwerwiegend.

Erscheinungen, die dem unimodalen Modell folgen, sind weder exotisch noch auf die Archäologie oder das Phänomen Zeit beschränkt. Andere Beispiele für unimodale Modelle bieten z. B. Pflanzen und Tiere, die für ihr Leben bestimmte Umweltbedingungen bevorzugen, d. h. eine bestimmte Temperatur, Feuchtigkeit, Lichtexposition, Bodensäure etc. Unter den für sie optimalen Bedingungen sind sie in der Natur häufig und werden seltener, wenn dieses Optimum verlassen wird, und zwar unabhängig davon, in welche Richtung vom Optimum abgewichen wird (z. B. sowohl deutlich kälter/nasser als auch deutlich wärmer/trockener). Entlang der Umweltbedingungen zeigt die Häufigkeit vieler Lebewesen ein unimodales Verhalten.

Eine andere willkommene Eigenschaft der CA ist ihre Robustheit. Sie ist voraussetzungsarm und kann auf viele Arten von Daten angewendet werden. Die CA kann mit Anwesenheits- und Abwesenheitsinformationen umgehen, Häufigkeiten (statistisch “Nominalskala”) oder Ränge (“Rangskala”) analysieren, aber auch auf Messwerte angewendet werden, während viele andere multivariate Verfahren Messwerte (“Intervallskala”, “Verhältnisskala”) erfordern. Dies ist ein weiterer Grund für die Beliebtheit der CA in der Archäologie, da hier oft Anwesenheits-/Abwesenheits-Beobachtungen oder Häufigkeiten vorliegen. Indes: die CA ist nicht auf die Archäologie begrenzt. Vielmehr ist sie auch in vielen anderen Wissenschaften eine beliebte statistische Methode, wie etwa in den Sozialwissenschaften, der Biologie oder Ökologie. Das bekannte Werk des französischen Soziologen Pierre Bourdieu “Die feinen Unterschiede. Kritik der gesellschaftlichen Urteilskraft” (1979, deutsch 1982) ist ein interessantes Beispiel für eine frühe Anwendung der CA in den Sozialwissenschaften.

Plant man die Anwendung multivariater Verfahren zur Analyse von Daten und ist unsicher, ob die Daten eher dem unimodalen Modell (Abb. 1) oder einem linearen Modell (Abb. 2) folgen, ist es nützlich, die methodischen Alternativen für lineare Modelle zu kennen. Angemessen und vergleichbar zur CA ist für lineare Daten die Hauptkomponentenanalyse (PCA) resp. Faktorenanalyse; sie ist – ähnlich der CA – ein ordnendes Verfahren, im Unterschied z. B. zu Clusteranalysen als gruppierende Verfahren. Die Anwendung einer Hauptkomponentenanalyse (PCA) auf unimodale Daten führt zu irrigen Ergebnissen, ebenso wie die Anwendung einer CA auf lineare Daten. In Kap. 12.5 werden wir uns dies an einem Beispiel anschauen. In der Praxis erweist sich die PCA als empfindlicher gegen leichte Verletzungen ihrer Anforderungen an die Daten, während die CA robuster gegenüber solchen Abweichungen vom idealen Modell ist.

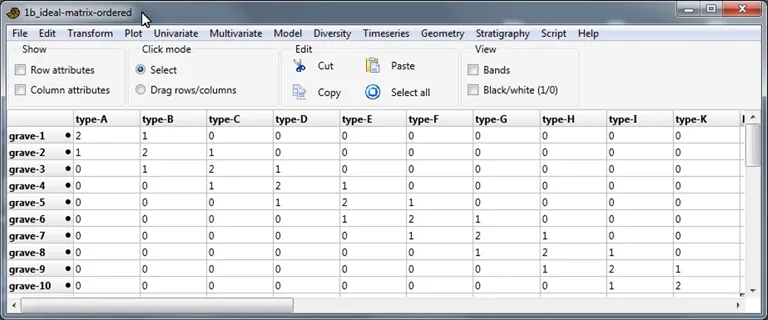
Abb. 3. Beispiel einer ideal diagonalisierten Tabelle (Matrix), in der die Zeilen und die Spalten dem unimodalen Modell folgen.

3 Theorie und Zielsetzung der Korrespondenzanalyse

Wirft man einen Blick auf den aktuellen (Sommer 2015) Artikel correspondence analysis in der englischsprachigen Wikipedia, erscheint die CA als etwas höchst Kompliziertes. Dieser Eindruck täuscht. Die CA ist einfach zu verstehen, zu rechnen und durchzuführen. Gleichwie, eine gründliche Einführung in die Theorie und die Berechnung ist hier nicht notwendig, denn es gibt gute weiterführende Bücher, die dies bereits leisten (Kap. 5). Das eigenhändige Rechnen oder Programmieren einer CA ist heutzutage ebensowenig nötig, weil es Computer und Software gibt, welche diese Aufgabe übernehmen (Kap. 4). Wir wollen uns daher zunächst darauf konzentrieren, die Zielsetzung der CA zu verstehen: Es geht darum, die Zeilen und Spalten einer gegebenen Tabelle so neu zu ordnen, dass die Zahlen in dieser Tabelle am Ende eine Diagonale bilden. Üblicherweise bestehen solche Tabellen (auch: Kontingenztafel, engl. contingency table) aus einer Vielzahl von leeren Zellen oder Nullen und wenigen anderen Zellen mit Einsen oder Häufigkeiten. Nach der Neuordnung der Tabelle sollten all diese Einsen resp. Häufigkeiten sich entlang einer Diagonalen in der Mitte der Tabelle häufen (Abb. 3). Mit Erreichen dieser neuen Ordnung folgen die Werte in den Zellen – jeweils zeilen- oder spaltenweise gelesen – dem unimodalen Modell: Jede Zeile und jede Spalte zeigt zunächst Nullen resp. leere Zellen, dann diverse Einsen oder Häufigkeiten, und anschließend wieder Nullen oder leere Zellen. Eine CA beginnt also mit einer ungeordneten Tabelle und ihr Ergebnis ist eine nach dem unimodalen Modell optimal neu geordnete Tabelle.

Unmittelbar nach Erfindung des Verfahrens geschah dieses Sortieren tatsächlich durch ein sukzessives mechanisches Umordnen der Zeilen und Spalten einer Tabelle mit der Hand. Zunächst wird die Ordnung der Zeilen optimiert, dann die der Spalten, dann wiederum die der Zeilen usw., bis sich eine stabile Lösung mit einer guten Diagonalen ergibt und das wiederholte Umordnen abgebrochen werden kann. Weil dabei die Position der Spalten oder Zeilen jedesmal wieder neu gemittelt wird, spricht man auch vom reciprocal averaging. Die ganze Methode wurde oft als Seriation (engl. seriation, ordination) oder als sequencing resp. sequence dating bezeichnet. Fotos einer konsequent ausgearbeiteten mechanischen Lösung dieser Aufgabe finden sich bei Périn (1980, Abb. 23). Die erste computergestützte Lösung für eine CA war nur eine Automatisierung dieses mechanischen Prozesses, d. h. per Computer wurde nach einem sehr einfachen Rechenverfahren (IHM 1983) eine wiederholte Umsortierung aller Zeilen und Spalten einer Tabelle vorgenommen (GOLDMANN 1972). Heutzutage ist das Rechenverfahren besser ausgearbeitet, mathematisch feinsinniger und beruht allein auf Berechnungen, d. h. erst am Ende des Verfahrens wird die Tabelle aufgrund der Ergebnisse einmal neu geordnet.

4 Software zur Durchführung einer Korrespondenzanalyse

Bei vielen der heute für eine CA verwendeten Computer-Programme handelt es sich um freie oder sogar quell-offene Software (Open Source), sodass dem Anwender keine besonderen Kosten entstehen. Man muss also nur lernen, mit diesen Programmen umzugehen. Die nachfolgend vorgestellte Liste ist eine persönliche Auswahl des Autors, der selbst sehr gründliche und langjährige Erfahrungen mit WinBASP und PAST besitzt. Alle genannten Programme werden mit guten Anleitungen verteilt, anhand derer ihre Bedienung leicht erlernbar ist. Ich empfehle sehr, die jeweiligen Handbücher eingehend zu studieren. Dieser Praxisleitfaden verwendet PAST für die praktischen Übungen, es sei jedoch betont, dass andere Softwarelösungen ebenfalls gut sind und jeweils spezifische Vorzüge haben. Näheres zur Software-Auswahl bietet Kap. 6.

Caveat: Dieser Text wurde im Sommer 2015 verfasst. Alle hier erwähnte Software resp. die Links dorthin wurden zuletzt im September 2015 benutzt und überprüft. Sollten sich danach insbes. die Links geändert haben, müssten es die verwendeten Begriffe ermöglichen, das Gesuchte mit den einschlägigen Suchmaschinen selbst schnell zu finden.

PAST 3.0: PAleontological STatistics Version 3.x (von Øyvind Hammer). Quelle: http://folk.uio.no/ohammer/past/

PAST 3.x wird vor allem für Computer unter MS-Windows entwickelt, es gibt...

Inhaltsverzeichnis

• Inhaltsverzeichnis
• Verzeichnis der Abbildungen
• 1 Zielsetzung
• 2 Einleitung
• 3 Theorie und Zielsetzung der Korrespondenzanalyse (CA)
• 4 Software zur Durchführung einer Korrespondenzanalyse
• 5 "Seriation" oder "Korrespondenzanalyse":Name der Methode und einführende Literatur
• 7 Der Start mit PAST
• 8 Einige Erläuterungen zu den statistischen Maßzahlen
• 9 Mehr Erfahrung gewinnen mit der CA
• 10 Zwei Beispiele mit echten archäologischen Datensätzen
• 11 "Der jüngste Typ datiert den Komplex" – oder: Was datiert die CA?
• 12 Start in eigene Projekte
• 13 Übernehmen der Ergebnisse einer vorliegenden CA
• 14 Schlussbemerkungen
• 15 Anregung für eine weiterführende Lektüre
• 16 Anregungen für weitere Trainingsfälle
• 17 Ziel erreicht
• Anhang: Das semi-automatische Sortieren großer Tabellen
• Abkürzungen
• Literatur
• Datensätze für die praktischen Übungen
• Über den Autor
• Danksagung
• Index
• Impressum