Mathematische Erzählungen

Geschichten mit grundlegenden Begriffen der Mathematik

Hans-Peter Zerlauth, Johannes Barton

• Verlag: Books on Demand
• Jahr: 2015
• ISBN drucken: 9783734799846
• eBook-ISBN: 9783739253800
• Auflage: 1
• Thema: Mathematik
• Thema: Mathematik Allgemein

»Über Mathematik sprechen und sie lesbar und erlebbar machen!« Unter diesem Motto erzählen Hans-Peter Zerlauth und Johannes Barton Geschichten, in denen Grenzwert, Steigung, Baumdiagramm, Rekursion, Ereignis & Co. die Hauptdarsteller sind. Diese Erzählungen streifen durch die mathematischen Gefilde der Folgen und Reihen, der Stochastik sowie der Differenzial- und Integralrechnung. Die »Mathematischen Erzählungen« richten sich an all jene, die an der Mathematik interessiert sind und Lust haben, einmal einen etwas anderen Blick auf mathematisch Bekanntes zu werfen. Zum Weiterlesen lädt die von Johannes Barton betreute Seite www.zbmathematik.at ein. Ein Band zu Zahlen, Vektoren und Funktionen ist unter dem Titel »Mathematik quergedacht« im Braumüller Verlag erschienen (ISBN 978-3-99100-013-6).

Die Pferdewette

Wie wir gesehen haben, sind die Objekte, welche wir mit der Wahrscheinlichkeitsrechnung untersuchen, Teilmengen, denen wir Wahrscheinlichkeiten, also Chancen zuordnen. Bevor wir uns allerdings einer solchen Zuordnung zuwenden, müssen wir feststellen, wie viele Teilmengen, an denen wir Interesse haben, in Frage kommen. Wir beginnen mit einem einfachen Beispiel und untersuchen ein Pferderennen, an dem acht Pferde (A, B, C, D, E, F, G, H) teilnehmen, nach den Gewinnchancen. Je weniger Information wir über Pferderennen haben, desto eher sind wir geneigt, jedem Pferd die gleichen Chancen einzuräumen. Nehmen wir als Ergebnismenge die Menge dieser acht Pferde und unterstellen wir einmal, dass uns zu Pferden nur der Begriff »Leberkäse« einfällt, dann werden wir jedem Pferd die Siegeswahrscheinlichkeit 1/8, also 12.5 %, zuordnen.

Laplace-Versuch

Eine Situation, bei der eine solche Gleichverteilung der Wahrscheinlichkeiten auftritt, wollen wir Laplace-Versuch nennen. Jedes mögliche Ergebnis eines solchen Versuches entspricht einem Element der Ergebnismenge und wird aus Symmetrie-gründen mit der gleichen Wahrscheinlichkeit wie die anderen Elemente belegt.

VERGLEICHENS –

Die Symmetrie eines Spielwürfels mit seinen sechs Möglichkeiten

– WERT

Um nun eine konkrete Wahrscheinlichkeit zu berechnen, müssen wir nur die Anzahl der uns interessierenden Elemente durch die Anzahl aller Elemente der Ergebnismenge dividieren. Beispielsweise bestimmt sich die Wahrscheinlichkeit, dass weder A noch B gewinnt, zu:

Nun gehen wir einen Schritt weiter und fragen nach den möglichen Platzierungen. Wollen wir auch diese Fragestellungen mit einem Laplace-Versuch beantworten, dann müssen wir eine andere Ergebnismenge zugrundelegen. Diese neue Ergebnismenge besteht aus allen möglichen Anordnungen, die wir mit den acht Pferden erzielen können.

ERINNERNS –

8! sprechen wir als »Acht Fakultät«

– WERT

Es gibt, als Fakultät angeschrieben,

mögliche Anordnungen.

Diese neue Ergebnismenge besteht also aus mehr als vierzigtausend Elementen. Kontrollieren wir diese Überlegungen anhand der Fragestellung: »Wie groß ist die Wahrscheinlichkeit, dass Pferd F gewinnt?« Das uns interessierende Ereignis ist dabei die Menge aller Anordnungen, bei denen das Pferd F an erster Stelle steht und diesen Platz gewissermaßen blockiert. Es gibt

BEACHTENS –

Anordnung

– WERT

Anordnungen für einen Zieleinlauf mit F als Sieger. Wie erwartet, wird die Fragestellung durch die Angabe der Wahrscheinlichkeit von 7! / 8! = 1/8 beantwortet. Offensichtlich sind wir jetzt in der Lage die Wahrscheinlichkeit für jede konkrete Belegung des Siegerpodestes, also der ersten drei Plätze, anzugeben. Wir denken uns beispielsweise Pferd F an der ersten, Pferd G an der zweiten und Pferd A an der dritten Stelle fixiert und erhalten so

mögliche Anordnungen und eine Wahrscheinlichkeit von

BEACHTENS –

Diese Frage kann auch ohne Laplace-Versuch, dafür aber mit bedingten Wahrscheinlichkeiten, behandelt werden.

– WERT

»Das sind ja nicht einmal 0.3 %!«, wird man vielleicht einwenden. »Bei so einer kleinen Wahrscheinlichkeit würde ich niemals wetten.« Um nun Pferdewetten schmackhaft zu machen, werden wir die Wahrscheinlichkeit etwas erhöhen. Dazu müssen wir nur das zu untersuchende Ereignis ein wenig umformulieren: »Wie groß ist die Wahrscheinlichkeit, dass die Pferde F, G und A am Siegespodest landen, und zwar unabhängig von der Reihenfolge?« Wir stellen fest, dass wir für Pferd F drei Plätze und daher für Pferd G nur noch zwei Plätze zur Verfügung haben. Für Pferd A bleibt jetzt nur noch ein Platz am Siegespodest übrig. Die restlichen Pferde, welche die Plätze vier bis acht belegen, können wir beliebig anordnen.

So ergibt sich die gesuchte Wahrscheinlichkeit zu:

Wir finden also die sechsfache Wahrscheinlichkeit von zuvor, da wir die drei ausgewählten Pferde auf sechs verschiedene Arten auf dem Siegerpodest anordnen können, wenn wir die Anordnung außer Acht lassen.

BEACHTENS –

In der Wahrscheinlichkeitsrechnung sprechen wir von Teilmengen, in der Statistik von Stichproben, im Alltag von Auswahlen.

– WERT

Abgesehen davon, dass man vielleicht auf dieses Ereignis wetten wird, haben wir auch aus mathematischer Sicht viel erreicht. Da wir nämlich zwischen Mengen (keine Anordnung der Elemente) und deren Anordnungen (der Anordnung von Elementen) wohl unterscheiden können, abstrahieren wir folgendermaßen: Wir haben die Wahrscheinlichkeit einer konkreten 3-elementigen Teilmenge, bei einer gegebenen 8-elementigen Grundmenge bestimmt und festgestellt, dass diese 1/56 ist. Da es sich dabei um einen Laplace-Versuch handelt, können wir behaupten, dass es

solcher Teilmengen gibt.

Wie so oft in der Mathematik können wir neue bzw. allgemeine Erkenntnisse gewinnen, wenn wir neue Bezeichnungen und Symbole verwenden. Eine n-elementige Menge hat

Binomialkoeffizient

k-elementige Teilmengen. Wir lesen das als »n über k« und nennen diese Anzahl an Teilmengen Binomialkoeffizient.

Nun sind wir in der Lage obiges Zahlenbeispiel durch die Formel

zu verallgemeinern und diese Formel auch induktiv zu beweisen.

Dazu benötigen wir einen allgemeinen Induktionsschritt, welchen wir uns beispielsweise so konstruieren können: Fokussieren wir unsere Betrachtungen auf ein konkretes Element, sagen wir das Element A unserer n-elementigen Grundmenge. Die k-elementigen Teilmengen können nun das Element A enthalten oder auch nicht. Um nun eine Teilmenge, welche A enthält, zu bestimmen, müssen wir aus den restlichen (n - 1) Elementen der Grundmenge (k - 1) Elemente auswählen. Mit unserer Schreibweise gibt es dazu

ERINNERNS –

Induktio...

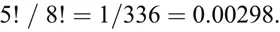
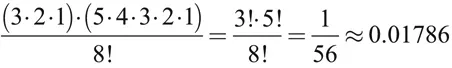
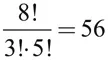
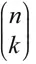
Inhaltsverzeichnis

• Inhaltsverzeichnis
• Vorwort
• Das Tagebuch
• Schriftschnitt
• Schriftart
• Schritt für Schritt
• Die Prognose
• Wer ist stärker?
• Der Brückenschlag
• Umkehrwachstum
• Grenzen erzwingen?
• Ein neuer Job
• Die Investition
• Bitte der Reihe nach!
• Der Tausch
• Schnitt für Schnitt
• Ein kurzer Blick zurück
• Das Netz
• Die Rückmeldung
• Wohnungssuche
• Jeder Fünfte schummelt?
• Das Wesen der Bäume
• No sports
• Vorsorgeuntersuchung
• Wie wird das Wetter?
• Die Pferdewette
• Die Sicherheit in unserer Stadt
• Die Bedeutung der Bedingung
• Ein stockdunkler Raum
• Ein kurzer Blick zurück
• Das Foto
• Punktgenau
• Die Satellitenschüssel
• Rüstzeug
• Das Versteck
• Kurvenfahrt
• Dumm gelaufen
• Der Reiz und die Empfindung
• Haben und Wollen
• Nachgefragt
• Ein kurzer Blick zurück
• Die Waage
• Vier Wände
• Temperatur
• Warum Flächen?
• Immer mehr – oder doch nicht?
• Es schneit!
• Was ist Fläche?
• Wie lange noch?
• Ausgefallen
• Berechnend
• Die kalte Reserve
• Ein kurzer Blick zurück
• Index
• Der letzte Gedanke
• Impressum