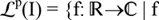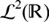Approximation der Lösungen von Differentialgleichungen mit Wavelets und Einstellung der Parameter

Marco Schuchmann

• Verlag: Books on Demand
• Jahr: 2019
• ISBN drucken: 9783739222134
• eBook-ISBN: 9783739268064
• Auflage: 2
• Thema: Mathematik
• Thema: Mathematik Allgemein

Die Modellierung physikalisch-technischer Fragestellungen führt oft zu numerischen Problemen, insbesondere zur numerischen Behandlung von Differentialgleichungen. Trotz des gewaltigenFortschrittes auf dem Gebiet der Computertechnologie ist man hier auf effiziente – aber auch gerade auf "robuste" – Verfahren angewiesen, die man auch auf steife oder instabile Probleme anwenden kann.In diesem Buch geht es um die Approximation von Lösungen von Differentialgleichungen mit Hilfe von Waveletbasen. Dabei muss die Differentialgleichung nicht in expliziter Formgegeben sein und es werden auch Differentialgleichungen höherer Ordnung, partielle Differentialgleichungen, wie auch Parameteridentifikationsprobleme betrachtet. Im ersten Teil des Buches werden Überlegungen zum Einstellen der Parameter angestellt, auf deren Basis dann ein adaptiver Algorithmus zum Lösen von Differentialgleichungen konstruiert wird. Dieser adaptive Algorithmus wurde im Rahmen eines Forschungsprojektes entwickelt.Danach wird das Lösen diverser Differentialgleichungen mit dieser Methode beschrieben und es wird gezeigt, dass bei einigen "kritischen" Testproblemen dieser adaptive Algorithmus stabiler als konventionelle Methoden ist (die u.a. in der Mathematica Funktion NDSolve implementiert wurden). Später wird aber auch auf die Approximation von Funktionen auf einem Kompaktum eingegangen, wo es einen Zusammenhang zur Fourieranalyse gibt.

1 Vorwort

Die Modellierung physikalisch-technischer Fragestellungen führt oft zu numerischen Problemen, insbesondere zur numerischen Behandlung von Differentialgleichungen. Trotz des gewaltigen Fortschrittes auf dem Gebiet der Computertechnologie ist man hier auf effiziente - aber auch gerade auf „robuste“ - Verfahren angewiesen, die man auch auf steife oder instabile Probleme anwenden kann.

Seit mehreren Jahren beschäftige ich mich mit der Approximation der Lösung von Differentialgleichungen mit Hilfe von Approximationsfunktionen, die über Vaterwavelets konstruiert werden. In den Jahren 2012 bis 2014 hatte ich hierzu ein Projekt geleitet, welches vom Zentrum für Forschung und Entwicklung (ZFE) der Hochschule Darmstadt finanziert wurde. Das Projekt trug im Jahr 2012 den Titel "Bestimmung der Parameter beim numerischen Lösen von Differentialgleichungen mit einem Wavelet-Kollokationsverfahren". Hier wurde von mir untersucht, wie man die verschiedenen Parameter, wie die Anzahl der Summanden bzw. der Basiselemente bei der Approximationsfunktion, die Anzahl der Stützstellen und auch den Parameter j, der Index des Raumes V_j der Multiskalenanalyse, dessen Basiselemente bei der Konstruktion der Approximationsfunktion verwendet werden, "optimal" wählen kann. Dabei wurde keine Voraussetzung an den Typ der Differentialgleichung gestellt. Weiterhin wurden mehrere Abschätzungen hergeleitet und es ergaben sich auch weitere Resultate, die zunächst nicht anvisiert wurden, die aber bei den Untersuchungen und Simulationen aufgefallen waren.

Die Vorarbeit für dieses Projekt und für die Veröffentlichungen in den Jahren 2013 und 2014 zu diesem Thema umfasst aber deutlich mehr Jahre. Seit dem Jahr 2000 beschäftige ich mich mit diesem Gebiet und habe hierzu diverse Projekte und Diplomarbeiten angeboten und auch Fachbücher veröffentlicht (siehe [82], oder auch [83] mit einem Kapitel von mir zum Thema Wavelets).

Nach den ersten Simulationen wurde anstelle eines klassischen Kollokationsverfahrens ein Verfahren verwendet, das etwas allgemeiner ist, da hier die Quadratsumme der Residuen minimiert wird. D.h., anstatt ein Gleichungssystem zu lösen und die Residuen an bestimmten Stellen gleich Null zu setzen, wird die Quadratsumme der Residuen an den Kollokationsstellen (wir behalten hier die Bezeichnung bei) minimiert, so dass man bei der Anzahl der Kollokationsstellen nicht eingeschränkt ist. Für eine bestimmte Anzahl von Kollokationsstellen ist dieses Verfahren wiederum äquivalent zu einem klassischen Kollokationsverfahren und in vielen Beispielen ist dieser Fall mit eingeschlossen. Wir sprechen der Einfachheit halber im Folgenden von einer Wavelet-Kollokationsmethode.

Im Rahmen des Projektes wurden verschiedene Typen von Differentialgleichungen mit diesem Verfahren approximativ gelöst, denn diese Methode kann man auf diverse Typen von Differentialgleichungen anwenden. Es wurde hierbei ein Indikator (dieser wird später öfter das Kriterium genannt, siehe Definition 4-1 von Q_a), der auf der Quadratsumme der Residuen basiert, gefunden, mit dem man erkennen kann, in wie weit einige gewählte Parameter des Verfahrens gut gesetzt wurden, wie die Anzahl der Stützstellen. Hier ergaben sich Zusammenhänge zwischen dem Approximationsfehler und dem Wert dieses Indikators in diversen Beispielen (wobei in den meisten Beispielen a = 2 gesetzt wurde). Dieser Indikator wird im 4. Kapitel näher untersucht. Auf der Basis dieses Indikators wurde ein adaptiver Algorithmus entwickelt, um die Parameter der Wavelet-Kollokationsmethode einzustellen (siehe Überlegungen dazu in Kapitel 4.2 bzw. 4.3 und den Algorithmus im Kapitel 4.4). Dieser wurde in ein Mathematica-Modul implementiert und getestet (siehe hierzu auch [V14]). Bei einigen Test-Differentialgleichungen lieferte dieser Algorithmus deutlich bessere Resultate als die Mathematica Funktion NDSolve, die auf diverse klassische (implizite und explizite) Methoden zurückgreift.

Für den Approximationsfehler konnten Abschätzungen mit Sätzen aus der numerischen Mathematik hergeleitet werden. Einige dieser Resultate wurden veröffentlicht (siehe Kapitel 16.2).

Es ergaben sich - neben den ursprünglich geplanten Forschungszielen - weitere Ergebnisse, wie beispielsweise jenes, dass man die Methode der Approximation bzw. die Wavelet-Kollokationsmethode auch zur Extrapolation verwenden kann. D.h., wenn man die Lösung einer Differentialgleichung beispielsweise mit dem Shannon-Wavelet auf einem Intervall approximiert hat, dann gibt es auch in einem größeren Bereich außerhalb des Approximationsintervalls nur relativ kleine Abweichungen zwischen der Approximationsfunktion und der exakten Lösung (siehe Kapitel 5.1.2 und Kapitel 15). Weitere Resultate ergaben sich beim Vergleich der Approximationen über die Wavelet-Kollokationsmethode mit denen der Orthogonalprojektion auf V_j (siehe Kapitel 10 und 13).

Eine ursprüngliche Idee von mir, bei der eine diskrete Wavelettransformation (DWT) zur Abschätzung der Verbesserung einer Lösung durchgeführt werden kann, wurde getestet (siehe Kapitel 4.2 und Kapitel 9). Da man aber mit dem Indikator eine Approximation relativ gut beurteilen kann, ist eine DWT nicht nötigt. Zudem müssen hier zusätzliche Voraussetzungen erfüllt sein.

Es konnten auch Parameter der Differentialgleichung (DGL) in den Beispielen aus der Reaktionskinetik (dies waren hier die Reaktionsgeschwindigkeiten) identifiziert (d.h. statistisch geschätzt) werden. Hier ergaben sich ebenfalls signifikante Zusammenhänge zwischen dem Wert des Kriteriums Q_a und dem Fehler bei der Identifikation in den Beispielen. Bei der Parameteridentifikation wurde auch eine Schätzung in zwei Schritten durchgeführt, die bei vielen Problemen - beispielsweise in der Reaktionskinetik - mit relativ geringem Aufwand durchgeführt werden kann (siehe Kapitel 7.2 und [V5]).

Bei den Simulationen wurden gewöhnliche Differentialgleichungen erster und zweiter Ordnung verwendet, wie auch Systeme und Differential-Algebraische Gleichungen. Hier konnten mit der Wavelet-Kollokationsmethode sehr gute Ergebnisse erzielt werden. Ebenso bei partiellen Differentialgleichungen. Der entwickelte adaptive Algorithmus wurde auf gewöhnliche Differentialgleichungen angewendet, später aber auch auf partielle Differentialgleichungen. Dazu wurde eine Masterarbeit vergeben. In dieser Masterarbeit wurden Parameter (Rendite und Volatilität) der Black-Scholes Differentialgleichungen identifiziert bzw. geschätzt und es wurde auch die Schätzung in zwei Schritten angewendet.

Im Rahmen der Untersuchungen ergaben sich einige Vorteile bei der Wavelet-Kollokationsmethode:

1. Man erhält eine Funktion als Lösungsapproximation und nicht nur Punkte. Diese Funktion kann man auch (in gewissen Bereichen) zur Extrapolation verwenden. Man benötigt in der Regel auch keine stückweise definierte Funktion wie bei der Kollokation mit Polynomen.
2. Bei der Anpassung an Messwerte - im Rahmen einer Parameteridentifikation in zwei Schritten - muss man keinen Funktionstyp vorgeben, wie bei einer konventionellen Regression.
3. Die DGL muss nicht in der Form y´ = f(y, t) vorliegen, sondern kann auch implizit gegeben sein (F(y´, y, t) = 0). Es kann auch eine DGL höherer Ordnung vorliegen, ein Randwertproblem oder ein Differential-Algebraisches System oder eine partielle Differentialgleichung. Die Methode wurde auch auf Integralgleichungen angewendet (siehe [V11]).
4. Die Parameteridentifikation kann mit geringerem Aufwand durchgeführt werden, wenn genügend Messwerte vorhanden sind, denn man kann hier die Schätzung in zwei Schritten durchführen. Hier wurde zusätzlich eine Abschätzung hergeleitet (siehe [V5] und Kapitel 7.2). Man kann diese aber auch „in einem Schritt“ durchführen.
5. Es ist auch eine Parameterschätzung bzw. Parameteridentifikation bei steifen Problemen möglich, sowie auch bei instabilen Problemen (siehe Beispiel von H.G. Bock, Kapitel 8.4).

Ein Nachteil ist der Aufwand, der sich aber allgemein bei impliziten Methoden ergibt, die aber bei steifen oder instabilen Problemen verwendet werden (müssen), wie auch bei Randwertproblemen.

Weiterhin ergab sich:

Insgesamt kann man mit dem Shannon-Wavelet gute Ergebnisse erzielen, auch wenn es keinen kompakten Träger besitzt. Hier kennt man auch gut die Bedeutung des Detailparameters j im Fourierraum, die sich über das Abtasttheorem von Shannon ergibt (siehe Kapitel 11). Man benötigt im Vergleich zu den Daubechies-Wavelets (Ordnung 5 bis 8) in den Beispielen mehr Koeffizienten, aber es wurde bei den Daubechies-Wavelets immer auch ein größerer Detailparameter j benötigt, was in der Hinsicht interessant ist, da die verwendeten Daubechies-Wavelets eine deutlich höhere Ordnung als das Shannon-Wavelet besitzen.

Mit dem Kriterium Q_a konnte in den Beispielen gut erkannt werden, in wie weit die Approximation "brauchbar" ist und bei Parameteridentifikationsproblemen, in wie weit die Schätzung gut war. Speziell ergab sich in diversen Simulationen sogar ein linearer Zusammenhang zwischen ln(Q₂) und ln(sse) (wobei sse die Quadratsumme der Approximationsfehler ist). Das Kriterium Q_a dient als Basis für den adaptiven Algorithmus und wurde auch theoretisch untersucht (im Kapitel 4.3). Bei dem Algorithmus kann man verschiedene Wavelets verwenden.

Eine wichtige Frage war auch die nach der Fehlerabschätzung bei der Approximation. Bei den Recherchen für diese Arbeit bzw. für das Forschungsprojekt wurde eine Reihe von Veröffentlichungen mit Fehlerabschätzung gefunden. Die meisten bezogen sich auf sogenannte interpolierende Wavelets. Bei vielen dieser Abschätzungen wird auch genau ein Typ von Differentialgleichung betrachtet (z.B. Randwertproblem 2. Ordnung), wie auch spezielle Wavelets. Eine Fehlerabschätzung für den Approximationsfehler in Abhängigkeit des Detailparameters j (und der Ordnung eines Wavelets) findet man in Kapitel 4.3, wobei beim Shannon-Wavelet ein direkter Bezug zum Fourierraum besteht (siehe auch Kapitel 11, 12 und [V15] und [V18]).

Es wurden Abschätzungen hergeleitet, die berücksichtigen, dass die Approximationsfunktion nicht über eine Orthogonalprojektion auf den Raum Vj berechnet wurde ("L²- Approximation"), sondern über die Minimierung der Residuen. D.h., hier wird berücksichtigt, dass die Approximationsfunktion - wie bei den meisten Anwendungen in dieser Arbeit - über eine Differentialgleichung bestimmt wurde und nicht über eine Orthogonalprojektion, wie bei vielen Abschätzungen, die "allgemein" aufgestellt wurden.

Hier gibt es einige Unterschiede, wenn man nur eine Approximation auf einem Kompaktum I bestimmt, was auch die Kapitel 10 und 13 zeigen. Bei Funktionen, die nicht auf

quadratisch integrabel sind, sondern nur auf einem Kompaktum I, kann man mit der Wavelet-Kollokationsmethode wesentlich bessere Approximationen erzielen, als wenn man

(mit Indikatorfunktion 1_I von I) orthogonal auf V_j projiziert, denn das "Abschneiden der Funktion y" hat i. Allg. negative Auswirkungen im Fourierraum (siehe Kapitel 10 und [V12]), so dass man i. Allg. ein deutlich größeres j für eine gute Approximation bei einer Orthogonalprojektion von

auf V_j benötigt. Die Orthogonalprojektion (mit dem Shannon- oder mit einem Daubechies-Wavelet) verhält sich bei einem solchen Typ von Funktion wie die Teilsumme einer Fourier-Reihe (siehe Kapitel 10, 13 und [V12] und [V19]).

2 Notationen

1)

ist messbar und

Wenn

dann nennen wir f quadratisch integrabel auf I. Für

schreiben wir später kurz

...

Inhaltsverzeichnis

• Inhaltsverzeichnis
• 1. Vorwort
• 2. Notationen
• 3. Kurze Zusammenfassung zur Multiskalenanalyse und zu Waveletbasen
• 4. Numerisches Lösen von gewöhnlichen Differentialgleichungen mit einer Wavelet-Kollokationsmethode
• 5. Beispiele zur Anwendung der Wavelet-Kollokationsmethode und zur Beurteilung einer Approximation
• 6. Problemstellung der Parameteridentifikation bei gewöhnlichen Differentialgleichungen
• 7. Konventionelle Methoden zum Lösen des Parameteridentifikationsproblems und Verwendung der Wavelet-Kollokationsmethode
• 8. Anwendung der Wavelet-Kollokationsmethode auf Parameteridentifikationsprobleme
• 9. Abschätzung der Verbesserung über eine DWT
• 10. Beispiel: Vergleich der Approximation der Kollokationsmethode mit der Orthogonalprojektion von 1[a,b]·y auf Vj
• 11. Shannons Abtasttheorem
• 12. Überlagerungen einer Funktion mit trigonometrischen Funktionen über eine MSA erkennen
• 13. Bessere Approximationen mit weniger Koeffizienten bei Anpassung an die DGL
• 14. Vergleich verschiedener Wavelets im Rahmen der Wavelet-Kollokationsmethode
• 15. Anhang: Vergleiche verschiedener Wavelets bei der Anwendung der Wavelet-Kollokationsmethode
• 16. Literaturverzeichnis
• Impressum