Neues verkehrswissenschaftliches Journal NVJ - Ausgabe 9

Entwicklung eines Algorithmus für die Kalibrierung von Modellen zur Betriebssimulation in spurgeführten Verkehrssystemen unter Berücksichtigung stochastischer Bedingungen DFG-Forschungsprojekt (MA 2326/9-1)

Yong Cui, Ullrich Martin, Weiting Zhao, Nan Cao

• Verlag: Books on Demand
• Jahr: 2015
• ISBN drucken: 9783735724366
• eBook-ISBN: 9783738682199
• Auflage: 1
• Thema: Technology & Engineering
• Thema: Engineering General

Simulationsverfahren unterstützen u.a. die Untersuchung und Planung von spurgeführten Verkehrssystemen, um Betriebsprogramme zu erstellen und die Effekte eines Betriebskonzepts zu bewerten. Die Qualität des Untersuchungsergebnisses bei Simulationsverfahren hängt von der Plausibilität des Simulationsmodells ab. Außerdem beschreibt der Ablauf der Kalibrierung des Modells den Betriebsprozess des Schienenverkehrs, sodass einzelne, dabei zu variierende Parameter von großer Relevanz sein können. Der hierzu entwickelte Algorithmus erreicht eine hinreichend gute Übereinstimmung des über Parameter beschriebenen Modells mit dem tatsächlichen Betriebsablauf in der Realität. Durch die Umsetzung des Algorithmus zum maschinellen Lernen wurde die Abweichung zwischen dem Simulationsmodell und der zu modellierenden Betriebsrealität in einem automatisierten iterativen Prozess minimiert und die Untersuchung und Planung von spurgeführten Verkehrssystemen durch ein realitätsnahes Simulationsmodell erheblich erleichtert.

1 Einleitung und Begriffe

Simulationsverfahren unterstützen u.a. die Untersuchung und Planung von spurgeführten Verkehrssystemen, um Betriebsprogramme zu erstellen und die Effekte eines Betriebskonzepts zu bewerten. Bei manuellen oder analytischen Methoden ist es schwer oder sogar unmöglich, die Wirkungen stochastisch beeinflusster Zugfahrten sowie der Interaktion zwischen den Zügen und der Infrastruktur eines komplexen Netzes hinreichend detailliert zu bestimmen. Deswegen werden Simulationssoftwares als experimentelle Tools bei Betriebsplanungen und Leistungsuntersuchungen eingesetzt.

Die Anwendung eines Simulationstools für spurgeführte Verkehrssysteme teilt sich in unterschiedliche Einzelprozesse auf: Erfassung der Infrastruktur, Erstellung eines Betriebsprogramms, Kalibrierung des Modells, Simulation und Auswertung. Dabei hängt die Qualität des Untersuchungsergebnisses bei Simulationsverfahren von der Plausibilität des Simulationsmodells ab. Außerdem beschreibt der Ablauf der Kalibrierung des Modells den Betriebsprozess des Schienenverkehrs, sodass einzelne, dabei zu variierende Parameter von großer Relevanz sein können. Die Parameter sind die Eingangswerte des Simulationsmodells für ein konkretes Anwendungsszenario. In der vorliegenden Arbeit werden die Anwendungsszenarien Betriebssimulation und Fahrplanerstellung bei der Modellkalibrierung berücksichtigt, um so die Plausibilität des Modells und die Qualität des Untersuchungsergebnisses durch Anpassung der Parameter sicherzustellen.

Zur Überprüfung der Plausibilität eines Simulationsmodells müssen Indikatoren definiert werden. Indikatoren sind Kenngrößen, die der Überprüfung der Plausibilität der jeweiligen Simulationsergebnisse dienen und in einem konkreten Anwendungsszenario (z. B. Betriebssimulation oder Fahrplanerstellung) relevant sind. D.h. die Kenngrößen aus den entsprechenden Simulationsergebnissen eines konkreten Anwendungsszenarios werden als Indikatoren betrachtet. Auf diese Arbeit bezogen bedeutet dies:

Zur Bewertung der Betriebsqualität werden die Verspätungen bei der durchgeführten Betriebssimulation betrachtet. Hierzu werden der Mittelwert und die Wahrscheinlichkeit der Verspätungen als Indikatoren verwendet.

Bei der Fahrplanerstellung werden die Sollfahrzeiten und Sollhaltezeiten abgebildet. Dafür werden die gebildeten Sollfahrzeiten und Sollhaltezeiten eines Fahrplans in einem Simulationsmodell als Indikatoren betrachtet.

Die Plausibilität der Simulationsergebnisse wird durch den Vergleich des Momentanwerts mit dem Zielwert der jeweiligen Indikatoren überprüft. Ein Momentanwert wird in Abhängigkeit von den eingegebenen Parametern ermittelt. Je nach Anwendungsszenario geschieht dies mit Hilfe von mathematischen Methoden oder mittels Auswertung von Simulationsergebnissen. Ein Zielwert ist der Wert des Indikators, der vom Simulationsmodell erreicht werden soll, d.h. der Momentanwert soll sich dem Zielwert durch die Kalibrierung angleichen. Die jeweilige Höhe des Zielwerts ergibt sich aus statistischen Erhebungen des realen Betriebsablaufs. Ein Simulationsmodell wird durch Anpassung der Parameter im Vergleich zwischen Momentanwert und Zielwert der Indikatoren kalibriert. Der Zusammenhang zwischen den Parametern und den Indikatoren bei einem Kalibrierungsprozess wird in Abbildung 1-1 dargestellt.

Abbildung 1-1:   Schema des Kalibrierungsprozesses

Um den erheblichen Aufwand bei der manuellen Kalibrierung zu reduzieren, wird in dieser Arbeit eine automatisierte Kalibrierungsmethode entwickelt. In Kapitel 2 werden zunächst der Aufwand bei Simulationsverfahren sowie die vorhandenen Forschungen und Anwendungen zur Modellkalibrierung erläutert.

Nach dem Anwendungsziel lassen sich die Simulationsaufgaben zum einen in Fahrplansimulation und zum anderen in Betriebssimulation unterscheiden. In einer Betriebssimulation werden die stochastischen Einflüsse durch den realen Betriebsablauf berücksichtigt. Hierfür besteht die Anforderung, die Störungsparameter, die in einem Simulationsmodell die stochastischen Einflüsse definieren, realitätsnah zu kalibrieren. In Ka-Kapitel 3 wird daher das Zielsystem für die Kalibrierung sowie der Algorithmus spezifiziert. Hieran anknüpfend und um die Effekte der Auswirkungen von unterschiedlichen Parametern zu bestimmen, wird eine Sensitivitätsanalyse in die Betrachtung einbezogen und die Auswahl der zu berücksichtigenden Parameter diskutiert. Der Aufwand der Kalibrierung wird reduziert, in dem nur die Parameter, die eine signifikante Auswirkung bei der Sensitivitätsanalyse zeigen, im Kalibrierungsprozess Berücksichtigung finden.

Bevor Fahrplan- und Betriebssimulationen durchgeführt werden können, müssen die Fahrpläne erforderlichenfalls auf der Grundlage eines Betriebskonzepts erstellt werden, da in vielen Fällen noch keine konkreten Fahrpläne vorhanden sind. Bei einem Kalibrierungsprozess werden nicht nur die Störungsparameter in einer Betriebssimulation, sondern auch die fahrplanbezogenen Parameter, die bei der Fahrplanerstellung beeinflusst werden, berücksichtigt. Der Algorithmus, der eine Anpassung der fahrplanbezogenen Parameter beinhaltet, wird daher in Kapitel 4 auf Grundlage von [ZHAO, 2012] diskutiert.

Die entwickelten Kalibrierungsmethoden können bei der Betriebssimulation und Fahrplanerstellung umgesetzt werden. Im darauffolgenden Kapitel 5 werden die Anforderungen, die Anwendungsfälle und die Systemarchitektur zur automatisierten Anwendung des Algorithmus spezifiziert. Zuletzt wird ein Ausblick auf weitere Forschungen und Entwicklungen in Kapitel 6 gegeben.

2 Grundlage der vorhandenen Forschung

Der Betriebsprozess in spurgeführten Verkehrssystemen unterliegt grundsätzlich stochastischen Einflüssen (vgl. u. a. [POTTHOFF, 1962]), die zu entsprechenden Abweichungen zwischen dem geplanten und dem tatsächlichen Betriebsablauf führen. Diese Gesetzmäßigkeiten werden in gängigen Simulationsmodellen und den darauf aufbauenden Simulationsprogrammen (vgl. u. a. RailSys [RMCON, 2010], LUKS [VIA CON, 2011], OpenTrack [OPENTRACK RAILWAY TECHNOLOGY LTD.]) durch eine Mehrfach- bzw. Betriebssimulation abgebildet.

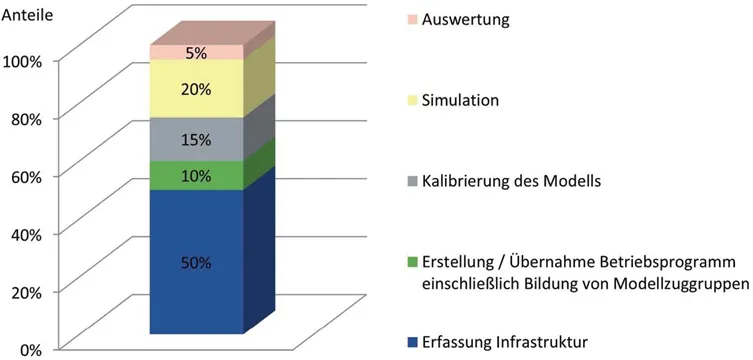
Abbildung 2-1 zeigt eine Übersicht der aus umfangreichen eigenen Erfahrungen abgeschätzten Aufwandsanteile bei der Anwendung von Modellen zur Betriebssimulation im spurgeführten Verkehr, wobei nachfolgend der Aufwand mit der Bearbeitungszeit gleichgesetzt wird. Dementsprechend entfallen auf die Kalibrierung etwa 15 von insgesamt 100 Zeitanteilen. Dieser Wert schwankt jedoch in Abhängigkeit von der konkreten Aufgabenstellung. Bei großer Inhomogenität bzw. Komplexität des Betriebsprogramms ist ein deutlich höherer Zeitanteil zu veranschlagen.

Abbildung 2-1: Aufwandsanteile bei der Anwendung von Modellen zur Betriebssimulation

Da bei der Auswertung bereits erhebliche Verbesserungen erreicht wurden (vgl. u. a. [MARTIN und SCHMIDT, 2010]), die Erstellung sowie Variation des Betriebsprogramms relativ komfortabel möglich sind und der Zeitbedarf für die Simulation selbst unmittelbar vom Entwicklungsstand der Rechentechnik abhängt, verbleibt wesentlich erschließbares Potenzi-Potenzial bei der Erfassung der Infrastruktur und der Kalibrierung.

Während bei den Modellen der Betriebssimulation des spurgeführten Verkehrs gegenwärtig noch „von Hand“ auf der Grundlage des Erfahrungsschatzes der Anwender kalibriert werden muss, gibt es bereits eine Reihe von Forschungsarbeiten zur automatisierten Kalibrierung von Modellparametern in der kurzfristig vorausschauenden Simulation des Betriebsablaufs und in anderen Fachgebieten.

HUANG und VERBRAECK beschreiben einen Algorithmus zur dynamischen, prozessnahen Kalibrierung auf der Grundlage einer quasi-kontinuierlichen Erfassung von Echtzeitdaten mit anschließender Parameterschätzung (vgl. u. a. [HUANG und VERBRAECK, 2009]). Der Aufwand diese Echtzeitdaten synthetisch im prozessfernen Simulationsprozess zusätzlich zu erzeugen und auszuwerten würde den Aufwand der Simulation deutlich erhöhen und den Zeitbedarf für die Simulationsläufe vergrößern, sodass das eigentliche Ziel einer aufwandsreduzierten Beschleunigung des Gesamtablaufs konterkariert werden würde.

In [HOMER et al., 1999] werden die primären Methoden zur Kalibrierung eines Parameters in spurgeführten Verkehrssystemen diskutiert. Anhand verwandter Beispiele wird gezeigt, dass die Kalibrierung ein iterativer Prozess ist. Daher werden eine Diskussion des kontinuierlichen Szenarios und eine zusätzliche Datenanalyse benötigt. Wenn nicht ausreichend Informationen vorliegen, um einen bestimmten Parameter mit akzeptabler Genauigkeit schätzen zu können, wird ein weiterer Arbeitsablauf der Teilmodellkallibrierung verwendet. Hierbei ist jedoch zu beachten, dass Teil- und Vollmodellkalibrierung jeweils zeitaufwändig sind.

Die Herausforderungen der Kalibrierung und Ansätze für ein- und zweigleisige Streckenabschnitte werden in [LINDFELDT, 2010] dargestellt. Bezogen auf die Kalibrierung sind die Rahmenbedingungen auf isoliert betrachteten Streckenabschnitten vergleichsweise einfach, da u. a. die Abhängigkeiten der Fahrten untereinander relativ klar strukturiert sind und die dispositiven Einflüsse überschaubar bleiben. Die in komplexeren Infrastrukturen zu beachtenden Verflechtungen und oftmals reflexiven Abhängigkeiten zwischen den Fahrten sowie die Variantenvielfalt bei Reihenfolgeänderungen sind kaum vorhanden und können demzufolge auch bei der Kalibrierung weitestgehend vernachlässigt werden.

Die Kalibrierung eines stochastischen Modells ist schwieriger als die eines deterministischen Modells, da bei letzterem Störungsparameter einen deutlich geringeren Einfluss auf das Simulationsergebnis haben und sie sich vorhersehbarer verhalten. In [SONG und JAMES, 1990] wird ein Verfahren beschrieben, mit dem die Verteilung eines einzelnen Parameters kalibriert werden kann. Monte-Carlo-Simulation und Bayesian-Ansatz werden bei diesem Verfahren genutzt, um Wasserläufe in Wassereinzugsgebieten zu kalibrieren.

Auch wenn eine unmittelbare Anwendung der vielfältigen und teilweise sehr umfangreichen Lösungen zur automatisierten Kalibrierung aus anderen Fachgebieten nicht möglich ist, sind doch die grundsätzlichen Erkenntnisse gleichermaßen für eine Anwendung im spurgeführten Verkehr gültig, sodass eine sinnvolle Adaption naheliegend ist.

Eine automatische Kalibrierung des Simulationsprozesses wurde bereits auch im Bereich des Straßenverkehrs entwickelt. In [SACKS et al., 2000] wird eine Testumgebung angewandt, um das Simulationsmodell CORSIM, das die Signal-Zeitpläne in einem Straßennetz von Chicago erzeugt, zu kalibrieren. Aufgrund von mangelhaften Beschreibungen des Fahrerverhaltens führt dieser Ansatz allerdings mitunter zu realitätsfernen Sperrungen von Kreuzungen und wegen des Mangels an genauen Daten zur Spurverteilung verfälscht das Verkehrsmodell die tatsächliche Situation. Die Kalibrierungsergebnisse werden deshalb nur mit einigen Einschränkungen verwendet. Ein mehrstufiges Kalibrierungsverfahren für die mikroskopische Verkehrssimulation wird dagegen in [CHU et al., 2004] beschrieben. Es kalibriert das Verkehrssimulationsmodell in vier Schritten. Die Genauigkeit der Kalibrierung hängt jedoch hauptsächlich von der Qualität der beobachteten Daten ab, sodass dies eine Unsicherheit im Kalibrierungsprozess darstellt.

In [TOLLKÜHN, 2006] wird ein lokaler Simplex-Algorithmus ¹ zur multiplen Parameterkalibrierung bei der Modellierung optischer Lithographieprozesse verwendet. Insbesondere der mathematische Ansatz regt zu einer Prüfung im Hinblick auf eine Anwendung im Rahmen des hier beantragten Forschungsprojekts an.

Die Entwicklung einer standardisierten und automatisierten Prozedur zur Kalibrierung und Datenanalyse auf Grundlage statistischer Berechnungsverfahren zur Systemkalibrierung von flugzeuggetragenen Laserscannersystemen wird in [SCHIELE, 2005] beschrieben. Das angewandte robuste Schätzverfahren unter Verwendung von geeigneten Referenzwerten bietet interessante Ansatzpunkte, die möglicherweise auch sehr sinnvoll bei der Kalibrierung von Modellen zur Betriebssimulation im spurgeführten Verkehr genutzt werden können.

Die statistische Analyse der Verspätungsverteilungen im spurgeführten Verkehr kann verwendet werden, um die fahrplanbezogenen Parameter genau vorherzusagen. Eine negative exponentielle Verteilung der Verspätungen wurde zuerst von [SCHWANHÄUßER, 1974] eingeführt. Diese beruht auf manuellen Probenergebnissen des realen Betriebspro-Betriebsprozesses. Auf dieser Grundlage können aus umfangreichen empirischen Betriebsdaten mittels statistischer Analyse Verspätungsverteilungen für automatische Beschreibungsmodelle bestimmt werden (vgl. u. a. [GÜTTLER, 2006]). Verschiedene Verteilungsmodelle werden verwendet, um die Zufälligkeit der Zugverspätungen zu erfassen. In [HANSEN und PACHL, 2008] wird beschrieben, wie geeignete Bertriebsmodelle ausgewählt werden, um die reale Variabilität für Zugverspätungen zu erfassen. Zwei statistische Methoden zur Schätzung der Parameter eines Verteilungsmodells werden hierbei erläutert. Jedoch ist bei diesen Methoden eine große Menge an realen Daten erforderlich.

Sensitivitätsanalysen wurden auch ausgiebig im Bereich der spurgeführten Verkehrssysteme angewandt, um die Anpassungsgüte und Robustheiten des Liniennetzes zu erhöhen, indem zunächst die Auswirkung der Änderung eines Parameters bestimmt, danach die benötigte Genauigkeit dieses Parameters ermittelt und zuletzt ein Bereich aufgestellt wird, bei dem die Änderung des Parameters das Ergebnis nicht mehr signifikant verändert.

In [ODIJK, 1999] wird die Sensitivitätsanalyse verwendet, um Robustheiten der entworfenen Gleisanlage in Bezug auf die genutzten Fahrpläne zu bestätigen. In diesem Zusammenhang wurde ein Algorithmus entwickelt, der einen gegebenen Fahrplan mittels Markow-Ketten stören kann.

In [OKE und CHARLES-OWABA, 2006] wird die Sensitivität eines Wartungszeitplans durch einen analytischen Ansatz geprüft. Die Sensitivitätsanalyse wird mit Hilfe eines optimalen anfänglichen Wartungszeitplans als Eingabewert in einem bestehenden Modell verwendet, um die Reaktionsfähigkeit der Modellparameter zu testen. Zur Erklärung einiger wichtiger Punkte, z.B. die Untersuchung der Beziehungen zwischen den Parametern des Modells und den Konvergenzkriterien des Modells, kann auf dieses Dokument verwiesen werden.

In [VILARINHO und TAVARES, 2012] werden verschiedene Analysen durchgeführt, um die Sensitivität eines Parameters anhand einzelner oder mehrerer Änderungen in einem mikroskopischen Verkehrsmodell zu erkennen. Die Wichtigkeit eines jeden Parameters im Verfahren der Verkehrsmodellierung wird beurteilt und das Ergebnis verwendet, um die relevanten Parameter für die Kalibrierung auszuwählen.

In [PALMA und MARCHAL, 2000] wird eine statische Quell-Ziel-Matrix entwickelt, um die Verkehrsnachfrage in dynamischen spurgeführten Verkehrssystemen zu modellieren, da die Verkehrsnachfrage ein bedeutender Parameter zur Bestimmung der Sollhaltezeit ist.

Auf der Grundlage einer arbeitsintensiven Felduntersuchung in Peking wird ein Modell der Sollhaltezeit in [ZHOU, 2011] vorgeschlagen. Darin wird insbesondere die Abhängigkeit der Sollhaltezeit von der Anzahl der ein- und aussteigenden Fahrgäste berücksichtigt. Jedoch sind gerade die lokalen Bedingungen die potenziellen Parameter des Modells, weshalb das in [ZHOU, 2011] entwickelte Modell nur für die operativen Linien Pekings gültig ist. Es kann deshalb kaum in anderen Städten ohne neue Felduntersuchung verwendet werden.

Durch eine automatisierte Kalibrierung für spurgeführte Verkehrssysteme wird der Aufwand bei einer Untersuchung mit Simulationsverfahren deutlich reduziert. In Kapitel 3 wird dies...

Inhaltsverzeichnis

• Vorwort
• Inhaltsverzeichnis
• Abbildungsverzeichnis
• Tabellenverzeichnis
• 1 Einleitung und Begriffe
• 2 Grundlage der vorhandenen Forschung
• 3 Kalibrierung von Störungsparametern für Betriebssimulationen
• 4 Kalibrierung von fahrplanbezogenen Parametern für Fahrplanerstellungen
• 5 Spezifikation zur automatisierten Anwendung des Algorithmus
• 6 Fazit
• 7 Glossar
• 8 Literaturverzeichnis
• Anhang I Verlauf des Kalibrierungsprozesses
• Anhang II Sensitivitätsanalyse der Störungsparameter
• Anhang III Berechnungsprozess des Ausgleichs
• Anhang IV Sequenzdiagramm der Sensitivitätsanalyse
• Anhang V Traceability-Diagramme
• Impressum