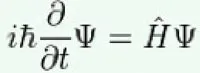Die faszinierende Welt der Quanten

Matthias Matting

• Verlag: AO Edition
• Jahr: 2013
• eBook-ISBN: 9783955770563
• Thema: Naturwissenschaften
• Thema: Quantentheorie

Eine Einladung auf eine Entdeckungstour zwischen Science Fiction und Mystik Die Quantenphysik steckt voller überraschender, seltsamer, ja befremdlicher Phänomene, die sich dem gesunden Menschenverstand zu entziehen scheinen. Teilchen, die sich an mehreren Orten zugleich befinden, ein Vakuum, das nicht leer ist, Computer, die rechnen, ohne die Aufgabe zu kennen, Systeme, über Milliarden Lichtjahre getrennt, die sich trotzdem gleichzeitig verändern: Selbst berühmte Forscher meinen manchmal, die Quantenphysik müsse sich irren. Oder sei zumindest generell unverständlich. Der Autor Matthias Matting, selbst Physiker, versucht, mit diesem Buch das Gegenteil zu beweisen. So widersinnig ihre Ergebnisse manchmal klingen, beschreibt die Quantenphysik unsere Wirklichkeit doch hervorragend. Dabei ist sie durchaus für Jedermann zu verstehen, auch ohne Mathematik-Studium. In einer klaren, unterhaltsamen Sprache beschreibt Matting die Phänomene, unterstützt von zahlreichen Fotos und Grafiken und einem umfangreichen Glossar. Eine Einladung auf eine Entdeckungstour, die zwischen Science Fiction und Mystik zu pendeln scheint – und doch eine der bestüberprüften Theorien der modernen Physik darstellt.

Superposition

Die Beschreibung der Realität mit Hilfe von Wellenfunktionen führt zuweilen zu bizarr anmutenden Schlussfolgerungen: Zur berüchtigten Schrödinger-Katze etwa, die so lange einen Zustand zwischen Leben und Tod einnimmt, bis jemand nachsieht.

Materie hat gleichzeitig Teilchen- und Wellencharakter, so viel wissen wir nun. Na und? Ein Lebkuchen schmeckt auch gleichzeitig süß und würzig, wo ist das Problem? Sehen wir uns dazu das im Kapitel 2 erwähnte Doppelspalt-Experiment noch einmal an. Da die quantenmechanische Wellenlänge von Weihnachtsgebäck zu klein ist, einen passenden Durchlass zu konstruieren, feuern wir zum Beispiel mit Elektronen auf die Anordnung. Auf dem Detektorschirm dahinter zeigen sich die typischen Interferenzmuster.

Die Wellenfunktion

Nun senken wir die Abschussfrequenz, und zwar derart, dass wir stets nur ein Teilchen auf die Reise schicken. Noch immer bleibt das Interferenzmuster erhalten. Klar, erinnern wir uns, das einzelne Elektron ist ja eine Welle, die mit sich selbst interferiert und gar keine zweite Welle braucht. Aber was heißt das für das Teilchen namens Elektron, das nach heutigem Wissen unteilbar ist und anders als etwa Neutronen nicht einmal aus Quarks besteht? Durch welchen Schlitz hat es sich bewegt?

Probehalber halten wir einfach den oberen Schlitz zu. Das Interferenzmuster verschwindet. Alle Elektronen treffen direkt hinter dem Loch auf den Detektor, sie fliegen in gerader Richtung, wie man es von einem Teilchen erwartet. Dasselbe passiert, wenn wir den unteren Durchlass schließen. Selbst wenn wir abwechselnd eines der beiden Löcher öffnen, kommen die Intensitäts-Maxima und -Minima auf dem Schirm nicht zustande. Durch unsere experimentelle Festlegung verhält sich das Elektron plötzlich wieder brav wie ein Teilchen und verzichtet auf die Interferenz.

Deshalb lassen wir nun beide Schlitze offen und nehmen einfach nur an, das Elektron sei diesmal durch den oberen Spalt geflogen. Ja, aber dann hätte es ja auch direkt hinter dem Durchlass auf den Detektor treffen müssen – ein Elektron fliegt schließlich nicht von sich aus einen Bogen, um uns den Gefallen zu tun, die Gesetze der Quantenphysik einzuhalten. Durch den oberen Spalt kann das Teilchen also nicht gekommen sein. Drehen wir das Gedankenexperiment um, fällt auch der untere Durchlass als Weg für das Elektron aus.

Das Dilemma bringt uns zu einer Schlussfolgerung, die in der klassischen Physik als völlig unsinnig abgetan werden müsste: Das unteilbare Elektron muss sich gleichzeitig durch beide Schlitze bewegt haben. Wenn wir ihm die Entscheidung durch Verschließen eines der beiden Wege abnehmen, wählt es schlichtweg beide auf einmal. Der gesunde Menschenverstand will sich mit dieser Folgerung zwar nicht so recht anfreunden. Aber das liegt ganz einfach daran, dass er in der Alltagswelt zuhause ist. Hier gelten die Gesetze der Quantenphysik zwar auch, doch sie nehmen so wenig Einfluss auf das Geschehen, dass wir davon nichts bemerken. Das ist nicht ungewöhnlich: Auch von den Regeln der Relativitätstheorie bekommt der Mensch im Alltag nichts mit. Oder ist Ihnen schon aufgefallen, dass die Zeit im Zug oder im Auto einen Hauch langsamer vergeht?

Trösten Sie sich am besten mit Nobelpreisträger Richard Feynman, der die Beschreibung der Wirklichkeit durch die Quantenphysik als „vom Standpunkt des gesunden Menschenverstands absurd“, aber doch als „vom Experiment in jedem Detail bestätigt“ beschrieb. „Ich hoffe“, meinte der Physik-Professor, „Sie können die Natur einfach als das akzeptieren, was sie ist: absurd.“

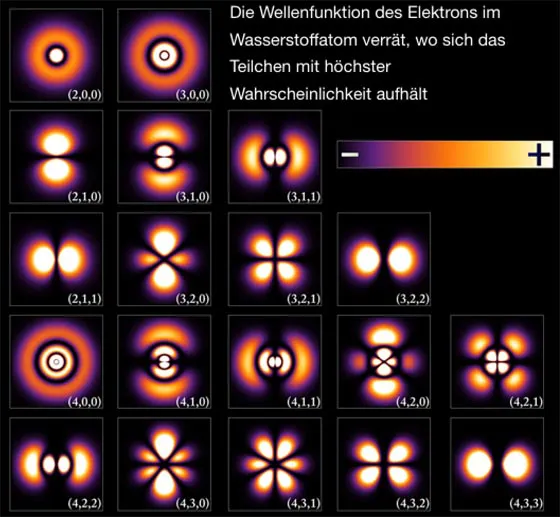
Bild 9: Die Wellenfunktion eines Elektrons in einem Wasserstoffatom. Messen würde man es mit höchster Wahrscheinlichkeit in einem der farbigen Tori. Das Proton sitzt im Zentrum der Grafik

Wie absurd sie wirklich ist, wird noch deutlicher, wenn wir das zulassen, was die Forscher als „delayed choice“ bezeichnen. Mit der „verzögerten Wahl“ ist die Strategie gemeint, einen der beiden Durchlässe des Doppelspalt-Experiments zuzuhalten (auch Öffnen funktioniert), nachdem (!) das Teilchen das Hindernis überwunden hat – aber bevor es auf dem Detektor erschienen ist. Das Experiment ist in anderer Form tatsächlich oft genug durchgeführt worden. Das Ergebnis widerspricht auf den ersten Blick der Kausalität: Für das Entstehen oder Wegbleiben der Interferenz ist unerheblich, wann genau wir die passenden Voraussetzungen geschaffen haben.

Solange der Detektor noch nicht angesprochen hat, können wir das Ergebnis des Versuchs noch beeinflussen. Der Physiker John Archibald Wheeler, auf den diese „delayed choice“-Experimente zurückgehen, trieb die Idee mit einem Gedankenexperiment auf die Spitze. Das Licht manch weit entfernter Himmelsobjekte, so genannter Quasare, erreicht uns nämlich doppelt. Das liegt daran, dass die Anziehungskraft massereicher Objekte zwischen dem Quasar und der Erde wie eine Linse wirkt. Bringt man im Experiment die einen unterschiedlichen Weg gegangenen Photonen wieder zusammen, lässt sich durch eine Veränderung des Experimentaufbaus auch noch Milliarden Jahre nach Reisebeginn der Lichtteilchen noch festlegen, welchen Weg diese genommen haben müssen.

Bild 10: Gedankenexperiment von John Archibald Wheeler: erst der Experimentator entscheidet, welchen Weg die vor Jahrmilliarden ausgesandten Photonen eines Quasars genommen haben müssen

Die Absurdität der Natur lässt sich in ein Wort und eine Formel fassen. Das magische Wort heißt „Superposition“: Damit bezeichnet man die grundlegende Eigenschaft jedes Quantensystems, in jedem seiner theoretisch möglichen Zustände gleichzeitig zu existieren. Die Wahrscheinlichkeit, das System bei einer Messung in einem ganz bestimmten Zustand anzutreffen, wird durch seine Wellenfunktion beschrieben. Dabei handelt es sich um eine komplexe Funktion, die auch imaginäre Anteile haben kann. Die Wahrscheinlichkeit, einen Parameter (etwa den Ort des Teilchens) mit einem bestimmten Wert vorzufinden, berechnet sich aus dem Quadrat des Betrags dieser Funktion. Aber Achtung: Es handelt sich nur um eine Wahrscheinlichkeit, nicht um eine exakte Vorhersage! Der Apfel fault sehr wahrscheinlich, wenn man ihn nicht aufhebt, aber er könnte auch frisch bleiben.

Dass sich Teilchen in dieser Weise verhalten, entzieht der Wissenschaft eine Grundlage der klassischen Physik, die nicht ohne Grund auch eine philosophische Seite hat: Es gibt in der Natur keine Vorbestimmung, keinen Determinismus. Selbst unter identischen Anfangsvoraussetzungen lässt sich das Ergebnis eines Prozesses nicht vorhersagen.

Dabei waren die Forscher doch seit dem Zeitalter der Aufklärung so stolz gewesen: Mit Hilfe der Newtonschen Mechanik sollte sich das komplexe Zusammenspiel des Kosmos bis ins kleinste Detail berechnen lassen. Wenn man nur die Anfangsbedingungen genau misst, kennt man das Schicksal jedes Systems. Die Quantenphysik macht dieser Auffassung einen Strich durch die Rechnung. Und zwar auf prinzipieller Ebene. Der Schmetterling, der im Amazonas-Regenwald mit den Flügeln schlägt und dadurch ein Gewitter in Berlin verursacht, er ist im Vergleich dazu ein klassisches Phänomen. Dass wir seinen Flügelschlag noch nicht in Wettermodelle einbeziehen können, liegt an unserer eigenen Unfähigkeit: So komplexe Rechnungen überfordern jeden Supercomputer, außerdem sind wir einfach nicht in der Lage, jeden einzelnen Schmetterling gleichzeitig zu erfassen.

Die Unsicherheit, die die Quantenphysik nun aber in die Natur einführt, ist von ganz anderer Qualität: Sie sagt, dass eine genaue Vorhersage prinzipiell unmöglich ist. Der Zufall, die Wahrscheinlichkeit, ist das bestimmende Element, das sich durch keinen Trick überwinden lässt. Das Universum ist eben kein kompliziertes Uhrwerk, für das Newton und seine Nachfolger es noch hielten. Ihnen kommt dieses Konzept ein wenig negativ vor? Selbst Albert Einstein, immerhin einer der Mitbegründer der Quantentheorie, war da ähnlich skeptisch: „Gott würfelt nicht“, beschrieb er mehrfach (unter anderem in einem Brief an Kollegen Niels Bohr) sein Unbehagen daran, dass die Quantentheorie der Physik die eindeutige Ursache-Wirkungs-Beziehung nimmt. Später werden Sie sehen, dass es sogar noch ein zweites Hindernis dafür gibt, die Entwicklung eines Quantensystems mit Sicherheit vorherzusagen...

Bild 11: Wellenfunktion des Elektrons im Wasserstoffatom

Die Schrödinger-Gleichung

Wie erhält man die Wellenfunktion eines Teilchens oder eines anderen Quantensystems, wie berechnet man sie? Dazu ist etwas erforderlich, was in der Schule immer sehr beliebt war: Das Lösen einer Gleichung, der Schrödinger-Gleichung. In diesem Fall handelt es sich um eine partielle Differentialgleichung.

Erinnern Sie sich noch an den Begriff „Ableitung“? Er tauchte im Mathematik-Unterricht auf, als es um Kurvendiskussionen ging. Das Maximum oder das Minimum einer Funktion lässt sich berechnen, indem man nach Stellen auf der Funktionskurve sucht, in denen der Anstieg gleich Null ist. Der Anstieg einer Funktion lässt sich aus ihrer ersten Ableitung berechnen – die erste Ableitung der Funktion f(x)=x2 ist zum Beispiel f‘(x)=2x. Eine Differentialgleichung ist eine Gleichung, deren Lösung (auch) von solchen Ableitungen der darin enthaltenen Funktionen abhängt. Wenn Ihnen das schon in der Schule Kopfzerbrechen bereitet hat – kein Problem, Sie müssen diese Gleichung nicht selbst lösen. In ihrer allgemeinsten Form lautet sie:

Dabei ist i die imaginäre Zahl (Wurzel aus -1), ħ (h-Strich) ist das Plancksche Wirkungsquantum, geteilt durch 2π. Ψ (Psi) ist die Wellenfunktion des Teilchens. Auf der linken Seite der Gleichung befindet sich die Wellenfunktion in ihrer Ableitung nach der Zeit (δ/δt) – sie beschreibt also, wie sich die Wellenfunktion mit der Zeit entwickelt.

Der auf der rechten Seite eingetragene Hamilton-Operator (das H mit dem Dach) beschreibt die physikalischen Verhältnisse des Systems, also etwa Impuls und Masse des Teilchens und die Kräfte, die darauf wirken. Der Hamilton-Operator ist insofern nur ein Dummy, eine Leerstelle, die die Physiker für konkrete Anwendungen mit den passenden Inhalten füllen müssen.

Die Schrödinger-Gleichung ähnelt insofern den klassischen Bewegungsgleichungen, die Sie aus der Schule kennen. Die klassische Gleichung x(t) = v*t etwa gibt den Ort eines Teilchens in Abhängigkeit von der Zeit an, wenn sich das Teilchen mit der Geschwindigkeit v bewegt. Die Wellenfunktion Ψ, also die Lösung der Schrödinger-Gleichung, bestimmt aber nicht nur einzelne Parameter wie den Ort – sie enthält alle (!) Eigenschaften eines Quantensystems zu einem bestimmten Zeitpunkt.

So einfach wie in der Schule ist die Bestimmung der Wellenfunktion (das heißt also das Lösen der Schrödinger-Gleichung) allerdings nicht. Die Physiker müssen sich dazu, von besonders einfachen Spezialfällen abgesehen, meist mit numerischen Methoden behelfen.

Dabei handelt es sich um mit Computerhilfe arbeitende Näherungsverfahren. Je nach Komplexität des Systems braucht man dazu sehr viel Rechenleistung – die Forscher sind deshalb sehr an so genannten Quantensimulatoren interessiert, die schwer erfassbare Systeme mit leichter kontrollierbaren Systemen simulieren (dazu später mehr).

Schrödingers Katze

Als Erwin Schrödinger seine Gleichung formulierte, war er selbst nicht sicher, was da eigentlich gerade entstand. Zunächst hatte er nur an einen Spezialfall gedacht – so wie ja auch Planck seine Ideen speziell für die Strahlung des Schwarzen Körpers entwickelte und selbst erstaunt war, als wie allgemeingültig sie sich erwiesen. Das Problem, das Schrödinger sah, bestand im Einfluss der Messung auf das Ergebnis. Wie kann es sein, dass ein solch subjektives Element wie ein Beobachter die Wirklichkeit definiert? Denn Welle hin oder her – ein Detektor misst das Elektron an einem ganz bestimmten Platz.

Hier vermutete Schrödinger ein fehlendes Element, eine versteckte Variable, die er mit einem berühmt gewordenen Gedankenexperiment aufzeigen wollte: Man stelle sich eine Katze in einer verschlossenen, nicht einsehbaren Kiste vor. Ebenfalls in der Kiste befindet sich eine Mord-Apparatur, die vom Zerfall eines radioaktiven Atoms gesteuert wird. Dieser Vorgang läuft komplett zufällig ab. Man kann zwar sagen, wie viele von 1000 Atomen binnen einer Stunde zerfallen werden. Doch es ist unmöglich, die restliche Lebenszeit für ein einzelnes Atom zu bestimmen. In welchem Zustand befindet sich die Katze?

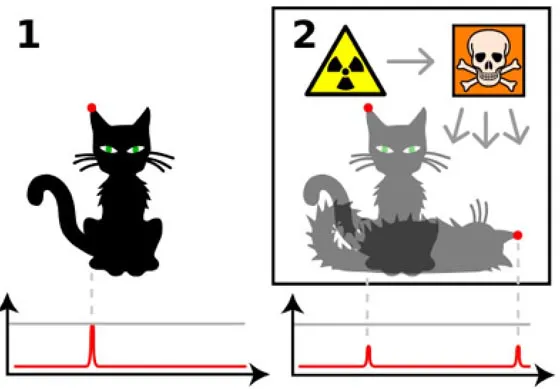
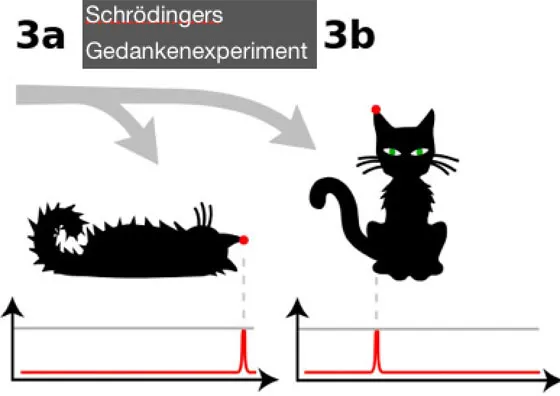
Aus Sicht der Quantentheorie könnte die Antwort lauten: In einer Überlagerung aus den beiden Zuständen „tot“ und „lebendig“. Die Wellenfunktion der Katze würde aussehen wie in Bild 2 der Zeichnung unten. Diese Superposition ist nicht mehr nachweisbar, wenn ein Beobachter die Kiste öffnet: Abhängig vom Zustand des Atoms in der Mordmaschine geht die Katze entweder in Zustand 3a oder 3b über.

Bild 12: Schrödingers Katze

Was das für unser Verständnis von der Wirklichkeit bedeutet, darüber waren sich die Quantenphysiker lange uneins. Die Kopenhagener Deutung etwa, 1927 von Niels Bohr und Werner Heisenberg in Kopenhagen formuliert, geht davon aus, dass die Wellenfunktion zum Zeitpunkt der Messung kollabiert – sie nimmt einen der möglichen Messwerte an. In ihrer extremsten Deutung wird die Katze also nicht durch das vom Kernzerfall aktivierte Giftgas getötet, sondern durch den Menschen, der die Kiste öffnet.

Viele Welten?

Eine alternative Erklärung bietet die Everettsche Viele-Welten-Theorie: Jeder mögliche Zustand wird na...

Inhaltsverzeichnis

• Inhaltsverzeichnis
• Die Welt im Kleinsten
• Teilchen-Welle-Dualismus
• Superposition
• Verschränkung
• Quanten-Kryptografie
• Quanten-Computer
• Quanten-Teleportation
• Das Vakuum ist nicht leer
• Impressum
• Glossar