La teoría del caos

Alberto Pérez Izquierdo

• Verlag: RBA Libros
• Jahr: 2019
• ISBN:
  9788491875291
• Thema: Ciencias biológicas
• Thema: Teoría de sistemas

En las primeras décadas del siglo XX, la física vivió dos grandes revoluciones: la teoría de la relatividad y la mecánica cuántica. En las últimas décadas, tuvo lugar otra revolución: la teoría del caos. Los científicos descubrieron que sistemas relativamente simples, cuya evolución estaba determinada por leyes precisas, podían mostrar un comportamiento irregular o caótico. Las claves del llamado efecto mariposa y la aparición de estructuras fractales son algunos de estos comportamientos tan impredecibles como fascinantes.LA GRAN PARADOJA DE LA FÍSICA.

¿Qué es el caos?

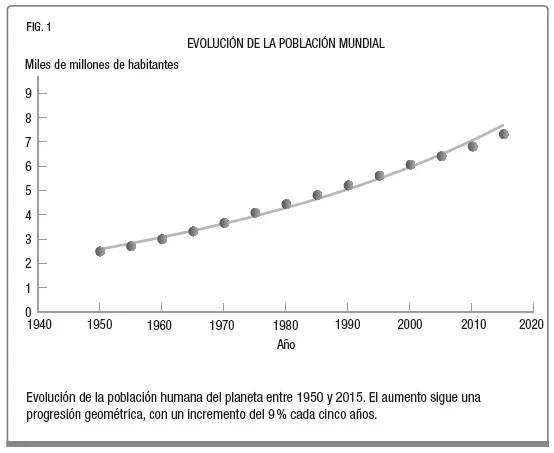
Entre los años 1950 y 2015, la población mundial pasó de 2500 millones a 7370 millones de personas. Dicha evolución se recoge en la gráfica de la figura 1. La línea continua trazada sobre la gráfica corresponde a un incremento exponencial de un 9% cada cinco años.

Esta evolución es el resultado de que la población, cada cinco años, se multiplica por un factor constante, lo que se refleja en la siguiente ley matemática:

x_n+1 = α x_n,

donde x_n es la población en un determinado año, x_n+1 es la población cinco años más tarde y α es una constante, que viene determinada por la tasa de crecimiento. En este caso, α vale aproximadamente 1,09. Si la población en 1960 era de 3000 millones de habitantes, en 1965 se acercaba a 1,09·3000=3270 millones.

Al multiplicarse por un factor constante cada vez, los valores de la población cada cinco años siguen una progresión geométrica y se disparan de forma exponencial. Este crecimiento exponencial de la población humana fue predicho por el pensador inglés Thomas Malthus en 1798. Malthus auguraba que la población, en ausencia de obstáculos, crecía según una progresión geométrica, de la forma α, α², α³, α⁴,… mientras que los recursos aumentarían en progresión aritmética, a la manera de la sucesión 1, 2, 3, 4,… Como la progresión geométrica crece mucho más deprisa que la aritmética, era solo cuestión de tiempo que la población humana empezara a toparse con dificultades si no se tomaban medidas para controlar el crecimiento.

En ausencia de factores limitantes, Malthus predecía que la población se doblaría cada 25 años. En la gráfica de la figura 1 vemos que eso no ocurre en la actualidad (se necesitan cerca de 40 años para duplicar la población mundial), pero lo que sí es cierto, en el intervalo analizado en esta gráfica, es que el aumento de la población sigue una progresión geométrica, con un incremento casi constante del 9% cada cinco años. Es decir, se cumple la ley de Malthus pero el coeficiente α es más pequeño de lo que él calculó.

La ley de Malthus es un caso particular de lo que en matemáticas se conoce como un sistema dinámico discreto. En general, un sistema dinámico es cualquier sistema cuyo estado cambia en el tiempo. La palabra sistema la debemos entender aquí en un sentido completamente general: puede tratarse de un conjunto de cuerpos celestes, el cuerpo humano, un ecosistema, la cotización de las acciones en la bolsa, etcétera. Para estudiar la evolución de un sistema dinámico se precisa una ley que nos diga cómo cambia con el tiempo. El sistema es discreto si esta ley proporciona el estado del sistema en intervalos fijos de tiempo, por ejemplo, el valor de las acciones cada día, o el de una población cada generación o cada cierto número de años, como en la figura 1. Si la ley proporciona el estado del sistema de instante en instante, para cualquier tiempo, se dice que el sistema es continuo.

Un sistema dinámico discreto viene definido por una variable x, que representa el estado del sistema (el número de individuos de la población mundial cada cinco años, en el ejemplo anterior), y una ecuación que dice cómo evoluciona el sistema:

x_{n + 1} = f(x_n) n = 1, 2, 3,…

La ley de evolución viene representada por f(x), una función matemática. Lo que expresa la ecuación anterior es que en cada iteración obtenemos el nuevo valor de x a partir del valor anterior. Para un valor inicial x0, la aplicación de f(x) (primera iteración) produce x₁=f(x₀). Una segunda aplicación, esta vez a x₁, produce x₂=f(x₁) (segunda iteración); haciéndolo una vez más obtenemos x₃ = f(x₂). De esta forma, la aplicación reiterada de f(x) produce una sucesión de valores x₀, x₁, x₂,… a partir de un valor inicial x0 dado. Por ejemplo, podemos construir un sistema dinámico sencillo duplicando a cada paso el valor de x. La función sería entonces f(x)=2x, y un valor inicial de la variable x₀ = 2 produciría la sucesión de valores 2, 4, 8, 16, 32,… Dando valores iniciales diferentes obtendríamos sucesiones diferentes, cada una correspondiente a una evolución posible del sistema. La figura 2 representa la función f(x)=2x, así como la evolución a la que da lugar su aplicación reiterada a partir del valor inicial 2.

En la teoría de Malthus f(x) es una función lineal: f(x)=α x, y su representación en una gráfica es una línea recta similar a la de la figura 2, aunque menos inclinada, porque el factor de crecimiento es menor que 2. Una función lineal tiene dos propiedades fundamentales:

1. Si multiplicamos la variable por un valor determinado el resultado queda multiplicado por el mismo valor:

f(k·x)= k·f(x).

2. La suma de dos valores da como resultado la suma de aplicar la función por separado a cada uno de ellos:

f(x₁+x₂)= f(x₁)+f(x₂).

En lo que nos ocupa en este libro, un sistema lineal nunca puede producir caos. En particular, la evolución propuesta por Malthus solo da lugar a tres comportamientos perfectamente predecibles. Si el factor α es mayor que 1, la población crece de manera exponencial, como en la figura 1, y a muy largo plazo se haría infinitamente grande. Si el factor α es menor que 1, la población disminuye en cada iteración de manera continuada; a muy largo plazo la población tiende a cero. Por último, si el valor α es igual a 1, la población no cambia. Un mundo lineal es un mundo perfectamente predecible, aburrido, cabría decir. Para que pasen cosas más interesantes, el comportamiento caótico entre ellas, las leyes que rigen los procesos naturales deben ser no lineales.

ROBERT MAY ESTUDIA LA DINÁMICA DE POBLACIONES

En 1976 un científico multidisciplinar, Robert May, estudió con detalle una modificación de la ley de Malthus que representaba un modelo más realista de la dinámica de poblaciones. May había estudiado Física en su Australia natal. Tras doctorarse en Física Teórica pasó un tiempo en Harvard como profesor de Matemática Aplicada, y en 1971 pasó un año en el Instituto de Estudios Avanzados de Princeton. Desde su fundación, el objetivo del instituto ha sido el de proporcionar a los científicos un ambiente relajado donde trabajar sin obligaciones, sin la presión de obtener resultados o completar proyectos en un plazo dado, una especie de «monasterio científico». En Princeton los científicos pueden embarcarse en proyectos que no lleven a ninguna parte, sin temor a ser expulsados. Allí May entabló relación con los biólogos de la universidad y empezó a interesarse por los problemas de la ecología teórica. May ofrece un claro ejemplo de hasta qué punto el caos determinista es un campo multidisciplinar. El sistema dinámico que él estudió ya había sido considerado por otros biólogos como modelo simplificado para la dinámica de poblaciones. Pero, donde otros vieron irregularidades y comportamientos extraños de dudoso interés, él vio algo que merecía la pena estudiar en detalle.

Como el propio Malthus había comprendido, el crecimiento exponencial no podía mantenerse indefinidamente. La falta de recursos limitaría necesariamente el crecimiento. Para tomar en cuenta este hecho, el modelo estudiado por May consideraba que el coeficiente α debía depender de la población, x, de modo que, a mayor población, menor tasa de crecimiento. May adoptó una forma en la que α, la tasa de crecimiento, decrece cuando crece la población, x, de una manera sencilla:

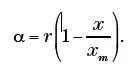
Es decir, si la población, x, es una fracción muy pequeña del valor constante x_m, α es esencialmente constante y su valor es muy próximo a r, que representa la tasa de crecimiento más alta posible. Por ejemplo, si x es una centésima parte de x_m, el número entre paréntesis vale 0,99 y α=0,99r. Pero a medida que crece la población, la tasa de crecimiento α va disminuyendo. Si la población es la mitad del valor x_m, es decir, x=0,5x_m, la tasa de crecimiento α disminuye a la mitad: r / 2. Por último, la tasa de crecimiento se hace cero para x=x_m. La constante x_m representa, pues, el máximo valor de población que el entorno puede admitir, ya que alcanzado este valor la población se extinguiría en el siguiente paso.

Para que la ecuación tenga un aspecto más manejable, vamos a redefinir la variable x de forma que represente no ya el número de individuos, sino la fracción entre el número de individuos existente y el total admisible, x_m. De esta forma, en adelante, x=1 representa una población con el número máximo de individuos, x_m; x=0,5 representa una población con la mitad del valor x_m, etcétera. Con este criterio, la ley de May se escribe así:

x_{n + 1}=r(1 – x_n)x_n.

Hay que entender esta ley como un modelo no solo de la población humana mundial, sino de cualquier especie en un ecosistema dado. Las diversas iteraciones corresponden a la población cada cierto intervalo fijo de tiempo, ya sean semanas, meses o años, pero también pueden referirse a sucesivas generaciones de individuos. Si la población es muy pequeña, se supone que hay suficiente alime...