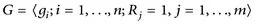The Elementary Theory of Groups

Benjamin Fine, Anthony Gaglione, Alexei Myasnikov, Gerhard Rosenberger, Dennis Spellman

• Verlag: De Gruyter
• Jahr: 2014
• ISBN:
  9783110382570
• Auflage: 1
• Thema: Matemáticas
• Thema: Álgebra abstracta

After being an open question for sixty years the Tarski conjecture was answered in the affirmative by Olga Kharlampovich and Alexei Myasnikov and independently by Zlil Sela. Both proofs involve long and complicated applications of algebraic geometry over free groups as well as an extension of methods to solve equations in free groups originally developed by Razborov. This book is an examination of the material on the general elementary theory of groups that is necessary to begin to understand the proofs. This material includes a complete exposition of the theory of fully residually free groups or limit groups as well a complete description of the algebraic geometry of free groups. Also included are introductory material on combinatorial and geometric group theory and first-order logic. There is then a short outline of the proof of the Tarski conjectures in the manner of Kharlampovich and Myasnikov.

1 Group theory and logic: introduction

1.1 Group theory and logic

The algebraic concept of a group and eventually the discipline of group theory arose in the early nineteenth century initially from the solution by Galois to the problem of solvability by radicals. This early work led primarily to finite groups and specifically to permutation groups, although as Cayley’s Theorem points out this is really no restriction. Later, infinite groups became prominent through their use in Geometry and Klein’s Erlanger Program (1876). Continuous groups were introduced by Lie and others to extend the methods of Galois for algebraic equations to the solutions of differential equations. Almost concurrently with the introduction of continuous groups, infinite discrete groups arose as tools in the study of combinatorial topology as introduced by Poincare. In addition, infinite discrete groups also became prominent in complex analysis via the work of Fricke and Klein on discrete groups of motions of the hyperbolic plane (Fuchsian groups). As these group objects were introduced through algebra, topology, geometry and analysis it became clear that there were strong interactions with formal logic. Each of the concrete examples of groups, mentioned above, permutation groups, matrix groups, groups of geometric transformations etc. are models in the sense of formal logic of abstract logical structures and languages. These ties became even clearer in the twentieth century as the study of mathematical logic became formalized.

This book will concentrate on the interactions between group theory and logic and will focus primarily on infinite discrete groups. We will deal with ideas and extensions of concepts arising around the Tarski Problems and their solution. The statements of the Tarski problems will be explained in the next section. First however we introduce some material that is needed to describe these problems.

The study of infinite discrete group theory essentially uses combinatorial group theory. This subdiscipline, within group theory, can roughly be described as the study of groups via group presentations. A presentation for a group G consists of a set of generators {g_v} for G from which any element of G can be generated as a word or expression in the {g_v} together with a set of relations on these generators from which any part of the group table can be constructed. In Chapter 2 we will examine combinatorial group theory in detail. Although a group presentation is a succinct way to express a group, it was clear from the beginnings of the discipline, that working with group presentations required some detailed algorithmic knowledge and certain decision questions.

In 1910 Max Dehn, as part of his work with group presentations for the fundamental groups of orientable surfaces, presented the three most fundamental decision problems. The first of these is the word problem or identity problem. This is given as follows:

(1) Word Problem: Suppose G is a group given by a finite presentation. Does there exist an algorithm to determine if an arbitrary word W in the generators of G defines the identity element of G?

Specifically if

is a finite presentation for G and W(g_v) is an arbitrary word in the generators of G, can one decide algorithmically, in a finite number of steps, whether W(g_v) represents the identity in G or not. If such an algorithm exists we say that G has a solvable word problem. If not, G has an unsolvable word problem. Dehn presented a geometric method to show that the fundamental group of an orientable surface of genus g ≥ 2, which we denote by S_g, has a solvable word problem. In particular he gave an algorithm which systematically reduced the length of any word equal to the identity in π(S_g). If a particular word’s length is greater than 1 and cannot be reduced then that word does not represent the identity. Such an algorithm is now called a Dehn algorithm. Subsequently small cancellation theory, (see Chapter 3), was developed to determine additional groups that have Dehn algorithms. More recently it was shown that finitely presented groups with Dehn algorithms are precisely the word-hyperbolic groups of Gromov (see Chapter 2). In 1955 Novikov ^[205] and independently Boone ^{[34] [35]} proved that, in general. the word problem is unsolvable, that is, there exist finitely presented groups with unsolvable word problems. Hence questions about word problems now focus on which particular classes of groups have solvable word problems. As decribed by Magnus (see ^[178]), given the Novikov-Boone result, any solution of the word problem is actually a triumph over nature.

The second fundamental decision problem is the conjugacy problem given by: (2) Conjugacy Problem: Suppose G is a group gi...