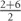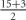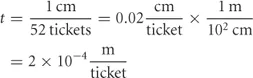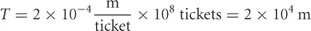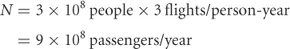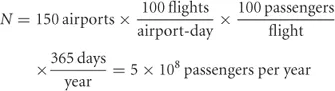![]()
Chapter 1
How to Solve Problems
For example, if it is 250 miles from New York to Boston, how long will it take to drive? You would immediately estimate that it should take about four or five hours, based on an average speed of 50–60 mph. This is enough information to decide whether or not you will drive to Boston for the weekend. If you do decide to drive, you will look at maps or the Internet and figure out the exact route and the exact expected driving time.
Similarly, before you go into a store, you usually know how much you are willing to spend. You might think it is reasonable to spend about $100 on an X-Game2. If you see it for $30, you will automatically buy it. If it sells for $300, you will automatically not buy it. Only if the price is around $100 will you have to think about whether to buy it.
We will apply the same reasoning here. We’ll try to estimate the answer to within a factor of ten. Why a factor of ten? Because that is good enough to make most decisions.
Once you have estimated the answer to a problem, the answer will fall into one of the three “Goldilocks” categories:
too big
too small
just right
If the answer is too big or too small, then you know what to do (e.g., buy the item, don’t drive to Boston). Only if the answer is just right will you need to put more work into solving the problem and refining the answer. (But that’s beyond the scope of this book. We just aim to help you estimate the answer to within a factor of ten.)
If all problems were as simple as that, you wouldn’t need this book. Many problems are too complicated for you to come up with an immediate correct answer. These problems will need to be broken down into smaller and smaller pieces. Eventually, the pieces will be small enough and simple enough that you can estimate an answer for each one. And so we come to
It is often easier to establish lower and upper bounds for a quantity than to estimate it directly. If we are trying to estimate, for example, how many circus clowns can fit into a Volkswagen Beetle, we know the answer must be more than one and less than 100. We could average the upper and lower bounds and use 50 for our estimate. This is not the best choice because it is a factor of 50 greater than our lower bound and only a factor of two lower than our upper bound.
Since we want our estimate to be the same factor away from our upper and lower bounds, we will use the geometric mean. To take the
approximate geometric mean of any two numbers, just average their coefficients and average their exponents.
∗ In the clown case, the geometric mean of one (10
0)
† and 100 (10
2) is 10 (10
1) because one is the average of the exponents zero and two. Similarly, the geometric mean of 2 × 10
15 and 6 × 10
3 is about 4 × 10
9 (because
and
)
∗ If the sum of the exponents is odd, it is a little more complicated. Then you should decrease the exponent sum by one so it is even, and multiply the final answer by three. Therefore, the geometric mean of one and 10
3 is 3 × 10
1 = 30.
EXAMPLE 1: MongaMillions Lottery Ticket Stack
Here’s a relatively straightforward example: Your chance of winning the MongaMillions lottery is one in 100 million.† If you stacked up all the possible different lottery tickets, how tall would this stack be? Which distance is this closest to: a tall building (100m or 300 ft), a small mountain (1000 m), Mt Everest (10,000 m), the height of the atmosphere (105 m), the distance from New York to Chicago (106 m), the diameter of the Earth (107 m), or the distance to the moon (4?108 m)? Imagine trying to pick the single winning ticket from a stack this high.
Let’s think about packs of paper in general. One ream of copier or printer paper (500 sheets) is about 1.5 to 2 in. (or about 5 cm since 1 in. = 2.5 cm) but paper is thinner than lottery tickets. A pack of 52 playing cards is also about 1 cm. That’s probably closer. This means that the thickness of one ticket is
Therefore, the thickness of 108 tickets is
2 × 104m is 20 kilometers or 20 km (which is about 15 miles since 1 mi = 1.6 km).
If stacked horizontally, it would take you four or five hours to walk that far.
If stacked vertically, it would be twice as high as Mt Everest (30,000 ft or 10 km) and twice as high as jumbo jets fly.
Now perhaps you used the thickness of regular paper so your stack is a few times shorter. Perhaps you used 1mm per ticket so your stack is a few times taller. Does it really matter whether the stack is 10 km or 50 km? Either way, your chance of pulling the single winning ticket from that stack is pretty darn small.
EXAMPLE 2: Flighty Americans
These problems are great fun because, first, we are not looking for an exact answer, and second, there are many different ways of estimating the answer. Here is a slightly harder question with multiple solutions.
How many airplane flights do Americans take in one year?
We can estimate this from the top down or from the bottom up. We can start with the number of airports or with the number of Americans.
Wow! Both methods agree within a factor of two.
The actual number of US domestic airline passengers in 2005 was 6.6 × 108, which is close enough to both answers.
EXAMPLE 3: Piano Tuners in Los Angeles
Now let’s work out a harder problem.
How many piano tuners are there in Los Angeles (or New York or Virginia Beach or your own city)? This is the classic example originated by Enrico Fermi [5] and used at the beginning of many physics courses because it requires employing the methods and reasoning used to attack these problems but does not need any physics concepts.
This means that we need to estimate the following:
population of Los Angeles
proportion of pianos per person
how often each piano is tuned per year
how much time it takes to tune each piano
how much time each piano tuner works per year
Let’s take it from the top.
The population of Los Angeles must be much less than 108 (since the population of the US is 3 × 108). It must be much more than 106 (since that is the size of an ordinary big city). We’ll estimate it at 107.
Pianos will be owned by individuals, schools, and houses of worship. About 10% of the population plays a musical instrument (it’s surely more than 1% and less than 1...