Optimierung in C++

Grundlagen und Algorithmen

Claus Richter

• Verlag: Wiley-VCH
• Jahr: 2016
• ISBN drucken:
  9783527341078
• eBook-ISBN:
  9783527800803
• Auflage: 1
• Thema: Mathematik
• Thema: Diskrete Mathematik

Die Optimierung ist einer der bedeutendsten Zweige der Mathematik mit weitreichenden Anwendungen in der Statistik, Physik, Meteorologie bis hin zur Wirtschaft und Unternehmensforschung. Ziel der Optimierung ist eine Minimierung oder Maximierung der im jeweiligen System relevanten Parameter unter einschränkenden Nebenbedingungen.

Praxisbezogen führt Claus Richter in die Algorithmen der Optimierung ein. Einsteiger und Fortgeschrittene werden gleichermaßen auf den heutigen Stand der Dinge gebracht. In klaren Schritten umreißt der Autor die Grundlagen dieses Gebietes, beginnend mit Definitionen und Optimalitätsbedingungen, um sich dann direkt an den C++-Programmierer zu wenden. Der nötige mathematische Apparat, die verwendete Programmiersprache C++ und ihre Klassen werden vorgestellt. Damit stellt der Autor ein einheitliches Niveau her und wird so einer breiten Leserschaft gerecht. Im Folgenden werden 20 Verfahren der linearen, quadratischen und nichtlinearen Optimierung behandelt und dem Anwender nähergebracht. Jeder Algorithmus wird im Aufbau erläutert und an einem konkreten Beispiel demonstriert. Fünf weitere Kapitel widmen sich anwendungsbezogenen Sachverhalten, u.a. der Parameteridentifikation, optimalen Steuerung und Strukturoptimierung. Durch die Bereitstellung der diskutierten Algorithmen und Beispiele als C++-Klassen gewährleistet das Buch einen optimalen Einstieg in die Optimierung.

Mit C++-Programmen zum Download unter www.wiley-vch.de/publish/dt/books/ISBN3-527-34107-2.

1
Einleitung

1.1 Das lineare und das nichtlineare Optimierungsproblem

Im vorliegenden Buch werden Optimierungsaufgaben betrachtet, die dadurch charakterisiert sind, dass eine lineare oder nichtlineare Zielfunktion f unter linearen oder nichtlinearen Ungleichungsnebenbedingungen minimiert wird, d. h.

(1.1)

wobei I

die Indexmenge der Ungeichungsrestriktionen bezeichnet. Gleichungsrestriktionen werden der Übersichtlichkeit halber zunächst weggelassen. An geeigneten Stellen werden sie zusätzlich berücksichtigt.

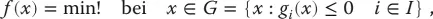
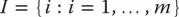
1.2 Definitionen und Bezeichnungen

Für die weiteren Überlegungen benötigen wir folgende Bezeichnungen:

• n-dimensionaler Euklidischer Raum: Rⁿ,
• Menge der reellen Zahlen: R,
• nichtnegativer Orthant des n-dimensionalen Euklidischen Raumes:
  
  ,
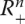
• Euklidische Norm:
  
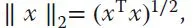
• Betragssummennorm:
  
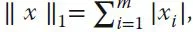
• (m, n)-Matrix A: rechteckiges Zahlenschema A = (a_i,j) von m ∗ n Zahlen, angeordnet in m Zeilen und n Spalten,
• quadratische Matrix: (m, n)-Matrix A mit m = n,
• Diagonalmatrix A: quadratische Matrix A mit a_{i j} = 0 für i ≠ j und a_ii ≠ 0,
• Einheitsmatrix I: Diagonalmatrix A mit a_ii = 1,
• obere Dreiecksmatrix A: quadratische Matrix A mit a_{i j} = 0, i > j,
• untere Dreiecksmatrix A: quadratische Matrix A mit a_{i j} = 0, i < j,
• positiv definite Matrix A: quadratische Matrix A mit x^TAx > 0 für alle x ≠ 0,
• symmetrische Matrix A: quadratische Matrix A mit a_{i j} = a_ji,
• transponierte Matrix A^T zu A: Matrix A^T mit A^T = (a_ji),
• inverse Matrix A⁻¹ zur Matrix A: Matrix mit der Eigenschaft A ∗ A⁻¹ = I,
• nichtsinguläre Matrix A: die inverse Matrix A⁻¹ zu A existiert,
• orthogonale Matrix A: Matrix mit der Eigenschaft A^T = A⁻¹,
• transponierter Vektor: x^T = (x₁, …, x_n),
• Gradient einer Funktion f : Rⁿ → R
  
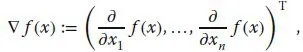
• Hesse-Matrix einer Funktion f : Rⁿ → R
  
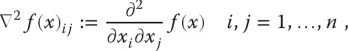
• Lagrang...

Inhaltsverzeichnis

• Cover
• Inhaltsverzeichnis
• Titel
• Autor
• Impressum
• Widmung
• Vorwort
• 1 Einleitung
• 2 Grundlagen
• 3 Mathematische Hilfsmittel
• 4 Probleme und Algorithmen als C++-Klassen
• 5 Lineare Optimierung
• 6 Quadratische Optimierung
• 7 Unbeschränkte nichtlineare Optimierung
• 8 Beschränkte nichtlineare Optimierung
• 9 Globalisierung
• 10 Innere-Punkte-Methoden
• 11 Parameteridentifikation
• 12 Optimale Steuerung
• 13 Form- und Strukturoptimierung
• 14 Optisoft – Ein C++-Softwaresystem zur Optimierung
• Anhang A: Referenzmanual
• Anhang B: Liste der Beispiele
• Literatur
• Stichwortverzeichnis
• End User License Agreement