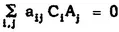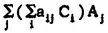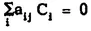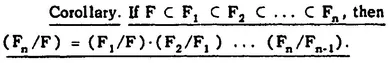Galois Theory

Lectures Delivered at the University of Notre Dame by Emil Artin (Notre Dame Mathematical Lectures,

Emil Artin, Arthur N. Milgram, Arthur N. Milgram

• Editorial: Dover Publications
• Año: 2012
• ISBN:
  9780486158259
• Categoría: Mathematik
• Categoría: Gruppentheorie

In the nineteenth century, French mathematician Evariste Galois developed the Galois theory of groups-one of the most penetrating concepts in modem mathematics. The elements of the theory are clearly presented in this second, revised edition of a volume of lectures delivered by noted mathematician Emil Artin. The book has been edited by Dr. Arthur N. Milgram, who has also supplemented the work with a Section on Applications.
The first section deals with linear algebra, including fields, vector spaces, homogeneous linear equations, determinants, and other topics. A second section considers extension fields, polynomials, algebraic elements, splitting fields, group characters, normal extensions, roots of unity, Noether equations, Jummer's fields, and more.
Dr. Milgram's section on applications discusses solvable groups, permutation groups, solution of equations by radicals, and other concepts.

II FIELD THEORY

A. Extension Fields.

If E is a field and F a subset of E which, under the operations of addition and multiplication in E, itself forms a field, that is, if F is a subfield of E, then we shall call E an extension of F. The relation of being an extension of F will be briefly designated by F ⊂ E. If α, β, γ, ... are elements of E, then by F(α, β, γ, ...) we shall mean the set of elements in E which can be expressed as quotients of polynomials in α, β, γ,... with coefficients in F. It is clear that

F(α, β, γ,...) is a field and is the smallest extension of F which contains the elements α, β, γ, ... . We shall call F(α, β, γ,...) the field obtained after the adjunction of the elements α, β, γ,... to F, or the field generated out of F by the elements α, β, γ,... In the sequel all fields will be assumed commutative.

If F ⊂ E, then ignoring the operation of multiplication defined between the elements of E, we may consider E as a vector space over F. By the degree of E over F, written (E/F), we shall mean the dimension of the vector space E over F. If (E/F) is finite, E will be called a finite extension.

THEOREM 6. If F, B, E are three fields such that F ⊂ B ⊂ E, then

(E/F) (B/F)(E/B).

Let A₁ , A₂, ..., A_r be elements of E which are linearly independent with respect to B and let C₁, C₂,..., C_s be elements of B which are independent with respect to F. Then the products C_i A_j where i = 1, 2, ... , s and j = 1, 2, ... , r are elements of E which are independent with respect to F. For if

, then

is a linear combination of the A_j with coefficients in B and because the A, were independent with respect to B we have

for each j. The independence of the C, with respect to F then requires that each a_ij = 0. Since there are r • s elements C_iA_j we have shown that for each r ≤ ( E/B ) and s ≤ ( B/F ) the degree ( E/F ) ≥ r

s. Therefore, ( E/F ) ≥ (B/F) (E/B). If one of the latter numbers is infinite, the theorem follows. If both ( E/B ) and ( B/F ) are finite, say r and s respectively, we may suppose that the A_j and the C_i are generating systems of E and B respectively, and we show that the set of products C_i A_j is a generating system of E over F. Each A

E can be expressed linearly in terms of the A_j with coefficients in B. Thus, A =

B_j A_j. Moreover, each B_j being an element of B can be expressed linearly with coefficients in F in terms of the C_i, i.e., B_j =

a_ij C_i, j = 1, 2, ... , r. Thus, A =

a_ij C_iA_j and the C_iA_j form an independent generating system of E over F.

B. Polynomials.

An expression of the form a_oxⁿ + a₁x^n–1+ ... + a_n is called a polynomial in F of degree n if the coefficients a_o, ... , a_n are elements of the field F and a_o ≠0. Multiplication and addition of polynomials are performed in the usual way³.

A polynomial in F is called reducible in F if it is equal to the product of two polynomials in F each of degree at least one. Polynomials which are not reducible in F are called irreducible in F.

If f(x) = g (x)

h(x) is a relation which holds between the polynomials f (x), g (x), h (x) in a field F, then we shall say that g (x) divides f(x) in F, or that g (x) is a factor of f (x). It is readily seen ...