El billar no es de vagos

Ciencia, juego y diversión

Carlos Bosch

• Editorial: Fondo de Cultura Económica
• Año: 2012
• ISBN del libro electrónico: 9786071603302
• Categoría: Matemáticas
• Categoría: Historia y filosofía de las matemáticas

Desde tiempos del cardenal Richelieu, cuando entre las habilidades de un mosquetero se incluía el saber jugar billar, hasta las películas como The Hustler y The Colour of Money, el billar siempre ha fascinado por su combinación de juego y ciencia. Carlos Bosch demuestra con abundancia de ejemplos y mediante la resolución de problemas geométricos y algebraicos que el billar merece utilizarse como una lúdica herramienta de razonamiento. El autor toma como punto de partida el regalo de un taco de billar para esbozar la historia de este juego y explicar sus nociones básicas y los detalles de su evolución.

IX. Cuarto sueño (otros billares)

En algún momento llegué a soñar con billares de formas rectangulares diversas, elípticas o de formas más caprichosas.

Las mesas de billar deben permitir que la bola rebote conforme a las leyes de reflexión; es decir, que en el punto donde toque la banda, el ángulo de entrada (incidencia) sea igual al ángulo de salida (reflexión) respecto de la tangente a la curva que delimita la mesa. Si la bola llega a algún punto donde no hay tangente, entonces se “muere”, es decir, su trayectoria termina en ese punto. Con un poco de imaginación podemos crear mesas de billar de forma arbitraria (figura IX.1).

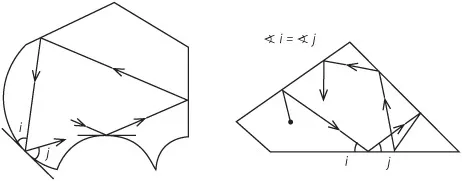
FIGURA IX.1

EL CÍRCULO

Una mesa de billar podría ser un círculo, un triángulo o un cuadrilátero, entre otras figuras posibles.

Dado un punto P, supondremos que es posible trazar la trayectoria que recorre la bola: PP₁P₂P₃... Si la bola no cae en un punto anguloso, se desplazará tanto tiempo como queramos. Puede darse el caso de que la trayectoria regrese a PP₁, en cuyo caso la bola repetirá el recorrido que ya se describió, por lo que se afirma que esta trayectoria es periódica. En términos geométricos, dichas trayectorias describen curvas cerradas, inscritas en la región determinada por la mesa de billar y que satisfacen la igualdad de los ángulos de incidencia y reflexión.

El billar con el que trabajaremos ahora será de forma circular. Hay varias preguntas que podemos formular a este respecto: ¿existen trayectorias periódicas?, ¿cuántas hay?, ¿cómo son?, ¿cómo reconocerlas?, ¿por dónde se desplaza la bola cuando recorre una trayectoria no periódica?

Consideremos una mesa de billar en forma de disco (figura IX.2); es decir, con frontera o “bandas” en forma de círculo, C. Las trayectorias van a estar perfectamente determinadas por la sucesión de puntos P₀P₁P₂P₃P₄P₅...

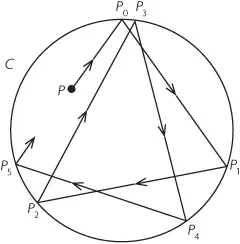
FIGURA IX.2

En cada uno de los puntos P_i tenemos la igualdad de los ángulos de incidencia y de reflexión. De esta propiedad se sigue que los segmentos P_{k − 1}P_k son iguales, pues los ángulos P_{k − 1}P_kM y P_{k − 1}P_kN son iguales, de manera que P_{k − 1}OP_k y P_kOP_k+1 también lo son, pues intersecan el mismo arco (figura IX.3).

Por lo tanto, P_{k − 1}P_k es igual a P_kP_{k + 1}. Cada vértice P_i se obtiene del anterior por una rotación de ángulo α y centro O, el centro del círculo. De manera que P_n se obtiene de P₀ por medio de una rotación de ángulo nα, de modo que la naturaleza de la trayectoria está totalmente determinada por el valor del ángulo α. Recordemos que es normal medir los ángulos en radianes, así que un ángulo de 360° corresponde a 2π radianes; es decir, a un giro completo. Por comodidad, α estará medido en radianes en todo lo que sigue.

Si α es conmensurable con 2π, es decir, si la razón α/2π es un número racional, entonces la trayectoria es periódica. Si α/2π es irracional, la trayectoria correspondiente es no periódica. En efecto, supongamos que α y 2π son conmensurables, es decir, que α = (m/n)2π, donde m y n son enteros. Entonces nα = 2mπ, y si se hace una rotación con un ángulo nα, se deja fijo cada pun...

Índice

• Portada
• ÍNDICE
• INTRODUCCIÓN
• I. El regalo
• II. Nunca falta alguien así...
• III. Primer sueño
• IV. De Luis XI a Paul Newman
• V. Segundo sueño
• VI. Ruedan y chocan
• VII. Tercer sueño (caminos mínimos)
• VIII. Los materiales
• IX. Cuarto sueño (otros billares)
• X. Las tablitas y otros problemas
• CONCLUSIÓN
• BIBLIOGRAFÍA