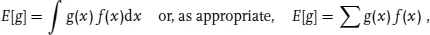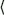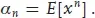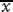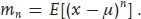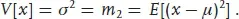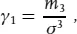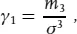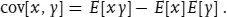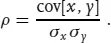Data Analysis in High Energy Physics

A Practical Guide to Statistical Methods

Olaf Behnke,Kevin Kröninger,Grégory Schott,Thomas Schörner-Sadenius

• Editorial: Wiley-VCH
• Año: 2013
• ISBN:
  9783527653430
• Edición: 1
• Categoría: Naturwissenschaften
• Categoría: Nuklearphysik

This practical guide covers the essential tasks in statistical data analysis encountered in high energy physics and provides comprehensive advice for typical questions and problems. The basic methods for inferring results from data are presented as well as tools for advanced tasks such as improving the signal-to-background ratio, correcting detector effects, determining systematics and many others. Concrete applications are discussed in analysis walkthroughs. Each chapter is supplemented by numerous examples and exercises and by a list of literature and relevant links. The book targets a broad readership at all career levels - from students to senior researchers. An accompanying website provides more algorithms as well as up-to-date information and links.

* Free solutions manual available for lecturers at www.wiley-vch.de/supplements/

1

Fundamental Concepts

Roger Barlow

1.1 Introduction

Particle physics is all about random behaviour. When two particles collide, or even when a single particle decays, we can’t predict with certainty what will happen, we can only give probabilities of the various different outcomes. Although we measure the lifetimes of unstable particles and quote them to high precision – for the τ lepton, for example, it is 0.290±0.001 ps – we cannot say exactly when a particular τ will decay: it may well be shorter or longer. Although we know the probabilities (called, in this context, branching ratios) for the different decay channels, we can’t predict how any particular τ will decay – to an electron, or a muon, or various hadrons.

Then, when particles travel through a detector system they excite electrons in random ways, in the gas molecules of a drift chamber or the valence band of semiconducting silicon, and these electrons will be collected and amplified in further random processes. Photons and phototubes are random at the most basic quantum level. The experiments with which we study the properties of the basic particles are random through and through, and a thorough knowledge of that fundamental randomness is essential for machine builders, for analysts, and for the understanding of the results they give.

It was not always like this. Classical physics was deterministic and predictable. Laplace could suggest a hypothetical demon who, aware of all the coordinates and velocities of all the particles in the Universe, could then predict all future events. But in today’s physics the demon is handicapped not only by the uncertainties of quantum mechanics – the impossibility of knowing both coordinates and velocities – but also by the greater understanding we now have of chaotic systems. For predicting the flight of cannonballs or the trajectories of comets it was assumed, as a matter of common sense, that although our imperfect information about the initial conditions gave rise to increasing inaccuracy in the predicted motion, better information would give rise to more accurate predictions, and that this process could continue without limit, getting as close as one needed (and could afford) to perfect prediction. We now know that this is not true even for some quite simple systems, such as the compound pendulum.

That is only one of the two ways that probability comes into our experiments. When a muon passes through a When a muon passes through a detector it may, with some probability, produce a signal in a drift chamber: the corresponding calculation is a prediction. Conversely a drift chamber signal may, with some probability, have been produced by a muon, or by some other particle, or just by random noise. To interpret such a signal is a process called inference. Prediction works forwards in time and inference works backwards. We use the same mathematical tool – probability – to cover both processes, and this causes occasional confusion. But the statistical processes of inference are, though less visibly dramatic, of vital concern for the analysis of experiments. Which is what this book is about.

1.2 Probability Density Functions

The outcomes of random processes may be described by a variable (or variables) which can be discrete or continuous, and a discrete variable can be quantitative or qualitative. For example, when a τ lepton decays it can produce a muon, an electron, or hadrons: that’s a qualitative difference. It may produce one, three or five charged particles: that’s quantitative and discrete. The visible energy (i.e. not counting neutrinos) may be between 0 and 1777 MeV: that’s quantitative and continuous.

The probability prediction for a variable x is given by a function: we can call it f(x). If x is discrete then f(x) is itself a probability. If x is continuous then f(x) has the dimensions of the inverse of x: it is ∫ f(x)dx that is the dimensionless probability, and f(x) is called a probability density function or pdf.¹⁾ There are clearly an infinite number of different pdfs and it is often convenient to summarise the properties of a particular pdf in a few numbers.

1.2.1 Expectation Values

If the variable x is quantitative then for any functiSpon g(x) one can form the average

(1.1)

where the integral (for continuous x) or the sum (for discrete x) covers the whole range of possible values. This is called the expectation value. It is also sometimes written

g

, as in quantum mechanics. It gives the mean, or average, value of g, which is not necessarily the most likely one – particularly if x is discrete.

1.2.2 Moments

For any pdf f(x), the integer powers of x have expectation values. These are called the (algebraic) moments and are defined as

(1.2)

The first moment, α₁, is called the mean or, more properly, arithmetic mean of the distribution; it is usually called µ and often written

. It acts as a key measure of location, in cases where the variable x is distributed with some known shape about a particular point.

Conversely there are cases where the shape is what matters, and the absolute location of the distribution is of little interest. For these it is useful to use the central moments

(1.3)

1.2.2.1 Variance

The second central moment is also known as the variance, and its square root as the standard deviation:

(1.4)

The variance is a measure of the width of a distribution. It is often easier to deal with algebraically whereas the standard deviation σ has the same dimensions as the variable x; which to use is a matter of personal choice. Broadly speaking, statisticians tend to use the variance whereas physicists tend to use the standard deviation.

1.2.2.2 Skew and Kurtosis

The third and fourth central moments are used to build shape-describing quantities known as skew and kurtosis (or curtosis):

(1.5)

(1.6)

Division by the appropriate power of σ makes these quantities dimensionless and thus independent of the scale of the distribution, as well as of its location. Any symmetric distribution has zero skew: distributions with positive skew have a tail towards higher values, and conversely negative skew distributions have a tail towards lower values. The Poisson distribution has a positive skew, the energy recorded by a calorimeter has a negative skew. A Gaussian has a kurtosis of zero – by definition, that’s why there is a ‘3’ in the formula. Distributions with positive kurtosis (which are called leptokurtic) have a wider tail than the equivalent Gaussian, more centralised or platykurtic distributions have negative kurtosis. The Breit–Wigner distribution is leptokurtic, as is Students t. The uniform distribution is platykurtic.

1.2.2.3 Covariance and Correlation

Suppose you have a pdf f(x, y) which is a function of two random variables, x and y. You can not only form moments for both x and y, but also for combinations, particularly the covariance

(1.7)

If the joint pdf is factorisable: f(x, y) = f_x(x) · f_y(y), then x and y are independent, and the covariance is zero (although the converse is not necessarily true: a zero covariance is a necessary but not a sufficient condition for two variables to be independent).

A dimensionless version of the covariance is the correlation ρ:

(1.8)

The magnitude of the correlation lies between 0 (uncor...