Quantum Optics for Engineers

F.J. Duarte

• Éditeur: CRC Press
• Année: 2017
• ISBN:
  9781351832618
• Édition: 1
• Sujet: Scienze fisiche
• Sous-sujet: Teoria quantistica

Quantum Optics for Engineers provides a transparent and methodical introduction to quantum optics via the Dirac's bra–ket notation with an emphasis on practical applications and basic aspects of quantum mechanics such as Heisenberg's uncertainty principle and Schrodinger's equation.

Self-contained and using mainly first-year calculus and algebra tools, the book:

• 
  
  

• Illustrates the interferometric quantum origin of fundamental optical principles such as diffraction, refraction, and reflection
• Provides a transparent introduction, via Dirac's notation, to the probability amplitude of quantum entanglement
• Explains applications of the probability amplitude of quantum entanglement to optical communications, quantum cryptography, quantum teleportation, and quantum computing.

Quantum Optics for Engineers is succinct, transparent, and practical, revealing the intriguing world of quantum entanglement via many practical examples. Ample illustrations are used throughout its presentation and the theory is presented in a methodical, detailed approach.

1

Introduction

1.1 Introduction

Perhaps no other subject in the history of physics has captured the human imagination more than quantum mechanics has. This captivation has extended beyond physics, and science, and well into the realm of popular culture. This is because quantum mechanics, also known as quantum physics, correctly describes the microworld and the nanoworld in a mathematical way that appears to be mysterious to us, the inhabitants of the classical world.

Perhaps one of the best, and most succinct, descriptions of quantum mechanics has been given by the well-known quantum and particle physicist John Clive Ward: “The inner mysteries of quantum mechanics require a willingness to extend one’s mental processes into a strange world of phantom possibilities, endlessly branching into more and more abstruse chains of coupled logical networks, endlessly extending themselves forward and even backwards in time” (Ward, 2004).

1.2 Brief Historical Perspective

Quantum mechanics came to light via the work of Max Planck, published in 1901. In that contribution, Planck used concepts of thermodynamics to explain the energy distribution of light sources as a function of wavelength (Planck, 1901). In doing so he introduced, without derivation, an equation where the energy of the emission was a function of frequency ν, that is,

$E=hv$

(1.1)

where

the units of the energy E is the joule (J)

the units of the frequency ν is the Hz

h is known as Planck’s constant (h = 6.62606957 × 10⁻³⁴ J s).

That was the birth of quantum mechanics. It was born from the experiment; it was an empirical birth.

Another important experimental observation relevant to the development of quantum mechanics was the photoelectric effect (Hertz, 1887). This effect, of fundamental significance to modern photomultipliers, and photo detectors in general, means that when a surface composed of charged particles is irradiated with light of frequency ν, there is a probability that electrons will be emitted from that surface. An explanation to the photoelectric effect was provided by Einstein (1905) via the relationship

$E=\hslash \text{ω}-W$

(1.2)

where W is defined as the work function or energy required to emit an electron from the irradiated surface. In this contribution, Einstein also proposed that light behaves as a stream of localized units of energy that he called lightquanta.

A few years later, Bohr (1913) postulated that electrons in an atom can only populate well-defined orbits at discrete energies W_n. When the electron jumps from one orbit of energy W_n to another one at W_n+1, it does so emitting radiation at a frequency ν, so that (Bohr, 1913)

$W_n-W_{n+1}=hv$

(1.3)

The developments introduced earlier were the preamble to the 1925–1927 revolution that yielded the quantum mechanics we know today. Heisenberg (1925), Born and Jordan (1925), and Born et al. (1926) introduced the quantum mechanics in matrix form. Schrödinger (1926) introduced his quantum wave equation. Dirac (1925) first established that there was a correspondence between Heisenberg’s non-commuting dynamical variables and the Poisson bracket (Dirac, 1925). Then he discovered that there was an equivalence between the Born–Jordan formulation and Schrödinger’s equation (Dirac, 1926). Further, he demonstrated that there was a direct correspondence between the Heisenberg–Dirac quantum mechanics and Schrödinger’s wave mechanics (Dirac, 1927).

In addition to the three formulations just mentioned, Dirac (1939) further introduced his bra–ket notation, also known as the Dirac notation, which is the preferred formulation of quantum mechanics used in this book.

Further approaches to quantum mechanics include the Feynman formulation via integral paths (Feynman and Hibbs, 1965) and the phase-space formulation (Moyal, 1949). There are also other lesser-known formulations.

Post quantum mechanical developments include quantum electrodynamics (Tomonaga, 1946; Schwinger, 1948; Dyson, 1949; Feynman, 1949), renormalization theory (Ward, 1950), Feynman diagrams (Feynman, 1949), and the standard model of particle physics (see, e.g., Salam and Ward, 1959, 1964; Glashow, 1961; Weinberg, 1967). The Higgs boson was theorized in 1964 (Higgs, 1964).

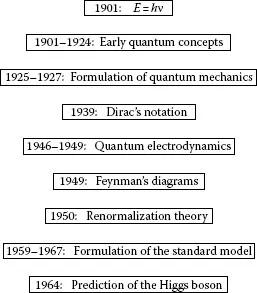
FIGURE 1.1
Time line depicting important developments in the quantum era.

Figure 1.1 provides a time line of important developments in the quantum era.

1.3 Principles of Quantum Mechanics

The Principles of Quantum Mechanics is the landmark book written by one of the creators of quantum mechanics Paul Adrien Maurice Dirac. The first edition of this masterpiece was published in 1930, the second edition in 1935, and the third edition in 1947. The fourth edition was released in 1958, and it is this edition that gives origin to the 1978 version, its ninth revised printing, used as the standard reference in this book.

An interesting aspect of this book is that the Dirac bra–ket notation was introduced in its third edition (1947). This is explained by the Australian particle physicist R. H. Dalitz (known of the Dalitz plot and the Dalitz pair) whom in 1947 was taking lectures from Dirac in Cambridge (Dalitz, 1987).

The Principles of Quantum Mechanics, third and fourth editions, are the vehicles by which the Dirac notation was introduced to physicists although Dirac first disclosed the notation in a paper entitled A new notation for quantum mechanics (Dirac, 1939). This paper, in a fairly mechanistic style, limits itself to introduce the new notation and to provide a correspondence between it and the “old notation.” The paper does not explain how Dirac discovered or created the new notation. Nor does he explain it in the book. At one time I did ask Dick Dalitz if Dirac had explained in his lectures how he created, or discovered, his bra–ket notation, and his reply was “no.”

Here we should make a necessary point: albeit we use as reference in this book, a revised version of the fourth edition of The Principles of Quantum Mechanics, we should be very much aware that the first edition was published in 1930 and that the Dirac notation was incorporated in 1947. Thus, given Dirac’s famous precision as a communicator, we should assume that our version of this masterpiece goes back to 1947.

Dirac’s book, The Principles of Quantum Mechanics, includes 12 chapters. The most relevant of those chapters to our immediate interest are

The principle of superposition

Dynamical variables and observables

Representations

The quantum conditions

The equations of motion

Perturbation theory

Systems containing several similar particles

Theory of radiation

Throughout the book he does use his bra–ket notation...