Didactiques: bilans et perspectives

Sonia El Euch, Audrey Groleau, Ghislain Samson

• Éditeur: Presses de l'Université du Québec
• Année: 2017
• ISBN de l'eBook: 9782760547926
• Sujet: Éducation
• Sujet: Éducation générale

Tout didacticien, peu importe la discipline à laquelle il est rattaché (mathématiques, sciences et technologies, langues maternelles, langues secondes ou étrangères, astronomie, arts, histoire, géographie, éthique et culture religieuse), s'engage fréquemment dans des discussions et des réflexions sur la didactique et ses origines et, plus particulièrement, sur les cours, la recherche et l'évolution des disciplines dans le contexte de la formation des futurs enseignants. Les origines de la didactique remontent à la philosophie grecque, précisément aux termes didaktos (enseigné, appris) et didaskw (enseigner, instruire, apprendre). Cette présence des deux pôles, à savoir l'enseignement et l'apprentissage, ne permettait pas à l'origine de différencier la didactique de la pédagogie. Progressivement, la didactique s'est distinguée de la pédagogie par le rôle central des contenus disciplinaires et par sa dimension épistémologique, c'est-à-dire par la nature des connaissances à enseigner. Ont ainsi vu le jour les didactiques disciplinaires, différentes de la didactique générale.Les auteurs du présent ouvrage rendent ici accessibles des connaissances issues de la recherche dans les différentes didactiques. Ce livre intéressera étudiants en éducation et professionnels de la didactique. Ils y trouveront des connaissances utiles à la formation et y découvriront le rôle de grandes figures dans chaque discipline.

PARTIE 1

LES MATHÉMATIQUES, LES SCIENCES ET LA TECHNOLOGIE

Chapitre 1

L’apport de la didactique des mathématiques au préscolaire

Vers une meilleure compréhension du programme de formation

Isabelle Deshaies

Les mathématiques constituent un vaste champ d’apprentissage qui nécessite de comprendre, de modifier ses représentations et de créer des liens pour retenir les nouvelles informations. Bien que ce processus semble simple en soi, de nombreuses recherches démontrent que depuis plusieurs années, de 6 à 7 % des élèves d’âge scolaire éprouvent de grandes difficultés en mathématiques (Charron et al., 2001 ; De Vriendt et Van Nieuwenhoven, 2010 ; Fuchs et Fuchs, 2005). Afin de mieux comprendre ces difficultés et d’en saisir les différentes sources, plusieurs chercheurs se sont penchés sur les études en didactique des mathématiques (p. ex. Brousseau, 1989 ; Deblois, 1996 ; Wozniak et Margolinas, 2009).

La didactique des mathématiques met en évidence le rôle primordial de l’enseignant comme médiateur entre l’élève et le savoir (Vergnaud, 1999). Pour parvenir à cette médiation, l’enseignant se doit de maîtriser chacune des connaissances à l’étude et ainsi d’être en mesure de fournir aux élèves des situations d’apprentissage leur permettant une réelle construction des savoirs. Pour une médiation réussie, l’enseignant doit aussi comprendre les difficultés d’apprentissage en mathématiques afin de les dissiper, à défaut de les prévenir. Une intervention ou une médiation réussie présuppose des réponses à la question suivante : quelles sont les notions que l’élève doit pouvoir mobiliser dès son entrée au préscolaire ?

Un nombre considérable d’études spécifient que les élèves en difficulté d’apprentissage sont plus lents dans les tâches élémentaires nécessitant des procédures mathématiques comme la lecture des nombres, la comparaison des nombres, la récitation d’une séquence de nombres et le dénombrement (Landerl, Bevan et Butterworth, 2004), de même que dans les tâches qui requièrent la manipulation de quantité de nombres (Rousselle et Noël, 2007) et la subitisation² de petites quantités numériques (Koontz et Berch, 1996). Ces études permettent de constater que les notions en jeu sont souvent celles qui devraient être acquises durant la période préscolaire ou dès les premières années de scolarisation. En fait, les recherches montrent non seulement que les premiers apprentissages en mathématiques jouent un rôle important dans le fait d’éprouver ou non des difficultés dans cette discipline, mais aussi que les habiletés précoces en mathématiques sont un important prédicteur de la réussite scolaire (Clark, Pritchard et Woodward, 2010 ; Duncan et al., 2007 ; Rourke et Conway, 1997). Les résultats de ces recherches en didactique des mathématiques trouvent-ils écho dans les programmes d’enseignement ?

Actuellement, le volet préscolaire du Programme de formation de l’école québécoise (PFEQ) du ministère de l’Éducation, du Loisir et du Sport (MELS) (2003) amène les élèves à développer huit types de connaissances mathématiques, soit : les jeux de nombres, le dénombrement, l’association, la comparaison, le regroupement et la classification, la régularité, l’estimation et la mesure. Ces connaissances laissent beaucoup de place à l’interprétation, et les notions qui leur sont associées ne sont pas suffisamment précises — d’où l’importance de s’y intéresser. Toutefois, une meilleure compréhension de la capacité naturelle des élèves à faire des mathématiques est essentielle afin de permettre à l’enseignant d’exercer son rôle de médiateur. À cet égard, les élèves du préscolaire détiendraient un sens inné des mathématiques : le sens des nombres (Dehaene, 2011). Selon l’auteur, celui-ci est lié à l’idée du sens approximatif des nombres et serait présent dès les premiers mois de vie des enfants. Il est en quelque sorte la fondation des apprentissages mathématiques ultérieurs chez l’élève.

Dans le texte qui suit, il sera donc question des éléments didactiques essentiels à la réussite des élèves en mathématiques préalables à l’enseignement formel et systématique, soit le sens des nombres, la subitisation, le comptage numérique et le dénombrement, la conservation du nombre et l’inclusion numérique (Dehaene, 2011 ; Deshaies, Miron et Masson, 2015). Ces différentes notions seront exposées dans une perspective didactique tout en faisant le lien avec la pratique enseignante au préscolaire. En terminant, et pour ouvrir de nouvelles pistes de recherche, il sera question de la contribution des neurosciences visant à outiller les élèves pour contrer leurs fausses conceptions lors de leurs apprentissages mathématiques.

1.1 Le sens des nombres

Le sens des nombres est l’idée selon laquelle l’être humain a une intuition de grandeur face aux quantités numériques (Dehaene, 2011). Ce sens des nombres permet de déterminer approximativement la quantité d’objets qui constituent un ensemble. Il permet également de déterminer, lors de la comparaison de deux ensembles d’objets, lequel en a le plus ou le moins, ou si ces deux ensembles sont d’égale valeur, sans avoir recours au dénombrement. L’acquisition du sens des nombres a des répercussions sur l’apprentissage du développement numérique, puisqu’il permet une meilleure appropriation du nombre symbolique (Dehaene, 2011 ; Deshaies, Miron et Masson, 2015), ce qui en fait un préalable essentiel à travailler dès le préscolaire.

Afin de mesurer la discrimination de grandeur numérique, les chercheurs utilisent un paradigme de comparaison de l’ampleur (De Smedt et al., 2013 ; Nosworthy et al., 2013). Dans ce type de tâches, les participants sont invités à choisir lequel des deux ensembles non symboliques est supérieur à l’autre. Deux effets ont été définis dans les études de la comparaison de grandeur (Ansari, 2008 ; Nosworthy et al., 2013) : l’effet de la distance numérique (EDN) et l’effet du rapport numérique (ERN).

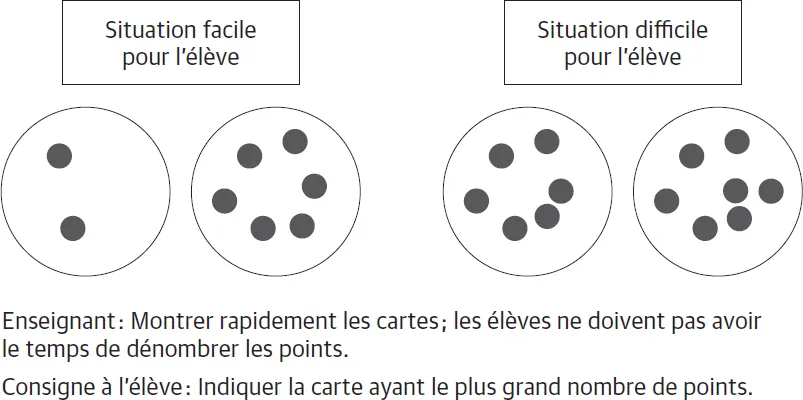
L’EDN est la facilité des individus à juger plus rapidement deux nombres lorsque ceux-ci sont numériquement éloignés (p. ex. 2 et 6) par rapport à ceux qui sont numériquement plus rapprochés (p. ex. 6 et 7). La figure 1.1 illustre une activité qui travaille l’EDN.

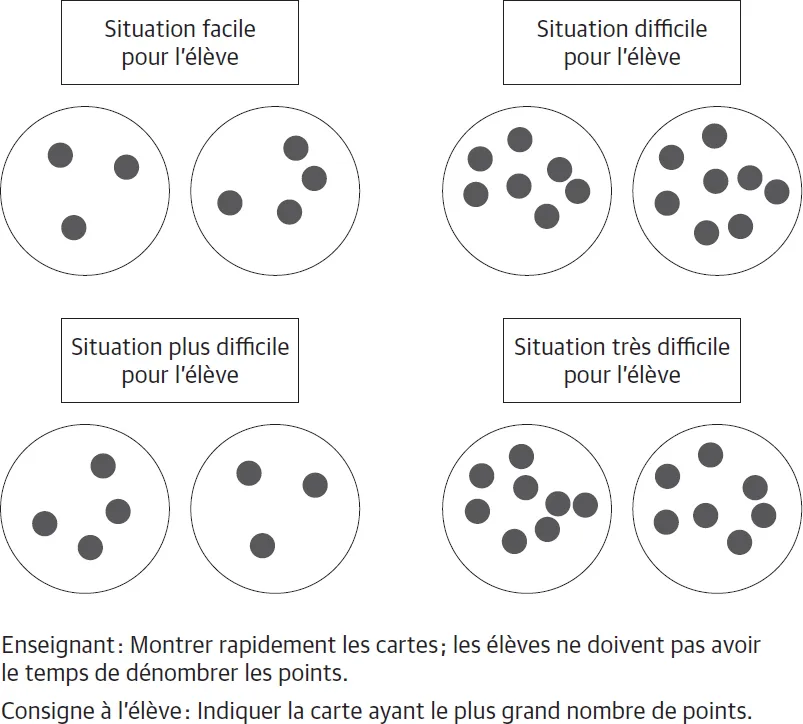
L’ERN est la facilité des participants à comparer plus rapidement et avec plus de précision deux nombres de moindre ampleur par rapport à deux nombres d’une grande ampleur, et ce, même lorsque la distance entre les nombres demeure constante (p. ex. la comparaison de 3 et 4 est plus facile que la comparaison de 7 et 8). De plus, il est plus facile de comparer deux ensembles qui, numériquement, sont placés de la plus petite valeur à la plus grande valeur que l’inverse (p. ex. comparer un ensemble de 5 points à un ensemble de 8 points est plus facile que de comparer un ensemble de 8 points à un ensemble de 5 points) (Ansari, 2008 ; Kolkman, Kroesbergen et Leseman, 2013 ; Soltész et Szűcs, 2014). La figure 1.2 illustre le concept d’ERN.

Figure 1.1 Exemple d’une activité travaillant l’effet de la distance numérique (EDN)³

Figure 1.2 Exemple d’une activité travaillant l’effet du rapport numérique (ERN)

En somme, le sens des nombres semble être à la base des compétences en arithmétique. Pour être capable de traiter un nombre (comparaison, calcul, etc.), il se révèle essentiel de connaître la magnitude⁴ que le nombre à l’étude représente (Nosworthy et al., 2013). Sans une compréhension de cette magnitude des nombres, l’association entre le nombre sous sa forme non symbolique et le nombre sous sa forme symbolique demeure un réel défi. Entre autres, les recherches de Piazza et ses collaborateurs (2014) et Dehaene (2011) démontrent que cette capacité numérique d’amplitude des nombres serait une aptitude importante dans le traitement des nombres et pourrait servir de base pour l’apprentissage de la signification numérique des chiffres arabes. Selon la recherche de Nosworthy et al. (2013), l’habileté à comparer des ensembles de points en prenant en considération l’EDN et l’ERN dès le préscolaire serait un prédicteur de réussite en mathématiques.

En pratique, en classe préscolaire, l’utilisation des cartes d’ensembles de points comme celles illustrées aux figures 1.1 et 1.2 permet de travailler le sens des nombres. Leur examen amène les élèves à comparer les deux ensembles en ayant seulement recours à leur sens approximatif des nombres. Cette activité peut également se vivre au début du premier cycle et permettra une transition vers l’acquisition des nombres symboliques (Dehaene, 2011).

Certaines applications logicielles permettent le travail sur le sens des nombres et l’inhibition. On peut, entre autres, consulter le site Panamath⁵ et le jeu Number Race⁶.

1.2 La subitisation

La subitisation est la perception intuitive, rapide et innée des petites quantités, sans avoir à recourir aux stratégies de comptage. En ce sens, très tôt, le jeune enfant reconnaît de un à quatre objets sans effectuer de comptage verbal (Butterworth, 2005 ; Butterworth et Dehaene, 1999 ; Piazza et al., 2002). Par contre, dès que la quantité dépasse quatre éléments, la perception intuitive devient plus lente et le risque d’erreurs augmente.

Ce processus naturel à tous les humains, soit celui de reconnaître les ensembles de nombres jusqu’à quatre sans avoir à dénombrer, est généralement connu sous le nom de « subitisation perceptuelle » (Clements, 1999 ; Gelman et Tucker, 1975). Toutefois, une deuxième forme de subitisation, cette fois-ci liée à la capacité de comptage, est présente. Elle est désignée par l’expression subitisation conceptuelle. La subitisation conceptuelle concerne la façon dont un individu reconnaît « une quantité entière comme le résultat de la reconnaissance de plus petites quantités, qui constituent le même ensemble » (Conderman, Jung et Hartman, 2014, p. 20). Plus généralement, elle peut être résumée comme la gestion systématique des numérosités perceptives (subitisation perceptuelle) pour faciliter la gestion des numérosités plus grandes (Obersteiner, Reiss et Ufer, 2013). Une illustration courante de la subitisation conceptuelle est perceptible lorsqu’on présente deux dés à un élève et qu’il doit déterminer le nombre de points sur ces deux dés ; par exemple, un dé de 3 et un dé de 4. La cardinalité de chacun de ces deux dés étant issue de la subitisation perceptuelle, la somme de ceux-ci, issue de la subitisation conceptuelle, amène l’émergence du 7.

En somme, l’habileté de subitisation est liée à la capacité de reconnaître et de manipuler des nombres spatialement (en utilisant, par exemple, des dés, des dominos, des boîtes de 10 et des doigts). Elle joue un rôle important dans le développement de la compréhension mathématique des enfants en lien à la fois avec les nombres et l’arithmétique (Mulligan et Mitchelmore, 2009 ; Van Nes et de Lange, 2007 ; Van Nes et Van Eerde, 2010). En plus d’être un outil puissant pour le développement de la compréhension générale des nombres chez les enfants (Penner-Wilger et al., 2007), la subitisation conceptuelle est liée positivement à une variété de résultats d’apprentissages particuliers au niveau du comptage et de la vitesse de comptage, ainsi que de la compréhension de la cardinalité (Baroody, 2004 ; Butterworth, 2005). La subitisation conceptuelle sous-tend la compréhension qu’ont les élèves de l’équivalence des différentes décompositions ou représentations des nombres (Van Nes et de Lange, 2007), la co...

Table des matières

• Couverture
• Titre
• Crédits
• Remerciements
• Liste des encadrés
• Liste des figures
• Liste des tableaux
• Liste des sigles
• Introduction – La pédagogie, la didactique générale et les didactiques disciplinaires
• Partie 1 – Les mathématiques, les sciences et la technologie
• Partie 2 – Les sciences humaines, les sciences sociales et les arts
• Partie 3 – L’interdisciplinarité en didactique
• Notices biographiques
• Notes