Les Mathématiques naturelles

Marc Chemillier

• Éditeur: Odile Jacob
• Année: 2007
• Imprimer l'ISBN: 9782738119025
• ISBN de l'eBook: 9782738186676
• Sujet: Mathematics
• Sujet: Mathematics General

Sait-on qu'un nœud de cravate ou encore des tresses correspondent à ce qu'on appelle un problème de topologie ? Il existerait donc des mathématiques « naturelles ». Marc Chemillier les a retrouvées dans les arts décoratifs des sociétés de tradition orale, dans leurs jeux de stratégie ou leurs techniques de divination. Ou encore, comme chez nous, dans la musique. Cette passionnante enquête ethnologique confirme que les mathématiques naturelles sont analogiques (tout le monde peut dire que 8 est plus grand que 7), quand les mathématiques formelles sont discursives (tout le monde ne sait pas forcément calculer 8+7). Un divertissement exotique qui fait mieux comprendre le fonctionnement de la pensée. Marc Chemillier, mathématicien et musicien, est maître de conférences à l'université de Caen et chercheur à l'Ircam. Retrouvez les animations et vidéos proposées par Marc Chemillier.

Chapitre 4

Musique (1) :
rythmes asymétriques

Dans la tradition musicale savante occidentale – cela vaut aussi pour les traditions savantes non occidentales, par exemple en Chine – la musique a toujours été associée aux mathématiques. En revanche, dans les sociétés dépourvues d’écriture, cette association semble plus surprenante. Cependant, il existe des répertoires musicaux issus de sociétés de tradition orale où l’on peut mettre en évidence des structures musicales complexes comparables à des constructions mathématiques. Ces exemples ouvrent un champ d’étude nouveau et important aux recherches en ethnomathématiques, qui ont porté jusqu’à présent plutôt sur les arts visuels, analysant la symétrie de figures ornementales et la topologie de tracés linéaires, ces propriétés formelles étant plus « visibles » que les propriétés par essence « invisibles » de la musique.

Parmi les idées musicales, une partie en effet ressemble à des idées mathématiques. Elles concernent plus particulièrement les formes et les structures musicales, et la ressemblance tient au fait que des opérations de type mathématique leur sont applicables. Prenons, par exemple, le cas des rythmes asymétriques aksak très répandus en Europe centrale, constitués de durées de deux et trois unités. C’est le cas du rythme turc transcrit en notation solfégique figure 4.1. Il se compose de croches dont certaines sont accentuées par les frappements d’un instrument de percussion qui introduit un groupement de ces croches par deux ou trois. On peut ainsi noter ce rythme comme une séquence de chiffres, soit 2223.

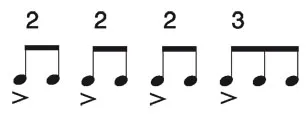
Figure 4.1 – Rythme asymétrique turc 2223.

De tels rythmes se prêtent à une opération mathématique simple qui est l’énumération. On peut en effet compter les combinaisons obtenues selon ce principe, c’est-à-dire toutes les séquences possibles de 2 et de 3. C’est ce que fait Constantin Brailoiu dans un article célèbre paru dans la Revue de musicologie69. Il commence par énumérer toutes les combinaisons obtenues avec deux chiffres : 22, 23, 32, 33, puis avec trois chiffres : 222, 223, 232, 322, 233, 323, 332, 333, et ainsi de suite jusqu’à neuf chiffres. Il obtient un tableau de 1884 séquences rythmiques distinctes. L’énumération est un exemple simple d’opération mathématique applicable à certaines structures musicales.

La musique dans les sociétés de tradition orale peut ainsi contribuer à la mise en évidence de représentations mathématiques. La situation est plus complexe que dans le cas des arts visuels étudiés au chapitre 2, en raison de l’absence de trace laissée par les productions musicales. Pour mettre en évidence des représentations mathématiques sous-jacentes, on est contraint de noter une trace visuelle de l’activité musicale (partition solfégique, sonagramme, etc.), comme on le fait habituellement en ethnomusicologie70. Cela dit, quels que soient leurs aspects visuels ou sonores, ces deux formes d’activités ont en commun d’être des activités motrices. C’est évident pour la musique instrumentale ; le cas de la musique vocale est un peu différent car elle mobilise le corps d’une manière plus intime71. On a vu que les représentations mathématiques des dessins sur le sable étaient directement liées à un geste, consistant à tracer un sillon sur le sable. Elles dépendaient finalement moins de la trace de ce geste – le dessin – que du geste lui-même : ne pas lever le doigt et ne pas repasser sur un segment déjà tracé.

Les exemples musicaux traités ici présentent certaines analogies. Par exemple, on étudiera dans ce chapitre des cellules rythmiques très caractéristiques des musiques traditionnelles africaines, constituées de durées de deux et trois unités, analogues aux rythmes aksak, mais d’une conception très différente. Nos analyses s’appuieront sur une représentation de ces cellules rythmiques en cercle, qui permet de traduire visuellement le fait qu’elles sont répétées indéfiniment en boucle. Mais ces cellules sont également liées étroitement à un geste. Lorsqu’elles sont jouées par un batteur qui frappe sur une poutre (comme on en verra un exemple plus loin avec le zoboko), celui-ci « monnaie » les durées de deux et trois unités contre des croches égales, comme on l’a vu pour le rythme turc. Cela signifie qu’il les divise en durées plus petites égales à l’unité (la croche), et qu’il groupe celles-ci par deux ou trois pour matérialiser les durées voulues. Concrètement, il frappe des coups réguliers en alternant les deux mains, mais il accentue certains coups plus que les autres, un sur deux ou trois selon le cas. Ainsi, le rythme 22323 sera joué très naturellement en faisant alterner les deux baguettes gauche et droite selon la succession g d + g d + g d d + g d + g d d (l’accent est alors joué par la main gauche notée g). Comme pour les dessins vanuatu, les propriétés mathématiques étudiées ici dépendent plus d’un geste que de la trace sonore de ce geste, ces propriétés étant d’ailleurs difficilement audibles, comme on pourra s’en rendre compte.

Des séries inégales de deux séparés par des trois

Notre premier exemple sera emprunté aux Pygmées Aka, un peuple de chasseurs-cueilleurs vivant dans la forêt tropicale, au sud-ouest de la République centrafricaine, dans la vallée de la rivière Lobaye. Cet exemple est tiré du cédérom réalisé par l’équipe de Simha Arom intitulé Pygmées Aka. Peuple et musique. Il s’agit d’une polyphonie vocale à quatre parties, soutenue par un soubassement polyrythmique. Cet accompagnement est très élaboré, il est joué par de nombreux instruments de percussions. Dans le tissu sonore complexe qui s’en dégage, une écoute attentive permet de percevoir une certaine structure rythmique particulière, jouée par des lames entrechoquées de machettes en fer, qui émerge discrètement de l’enchevêtrement des parties frappées par les autres instruments tout en restant un peu cachée (figure 4.2).

Cette séquence a une propriété intéressante, qui se traduit par une espèce de décalage causé par des petites valeurs (les croches) insérées dans une succession d’attaques à l’apparence plutôt régulière (les noires). La durée de cette petite valeur est grosso modo la moitié de la durée des autres et, si on la regroupe avec celle qui la suit immédiatement, elles forment toutes deux un groupe de trois unités (les noires pointées ajoutées sous la séquence, figure 4.2). On a ainsi des durées de trois unités, qui sont insérées dans des séries de durées de deux unités. Si l’on regarde comment sont réparties les durées de deux unités, on observe là aussi une irrégularité, car elles sont groupées par quatre d’un côté et par cinq de l’autre, la même alternance étant reproduite indéfiniment. Ces cellules rythmiques très particulières ont été mises en évidence par l’ethno-musicologue Simha Arom. Elles sont extrêmement fréquentes dans cette région d’Afrique, on en trouve différents modèles regroupés dans le tableau ci-après avec les populations qui pratiquent ces rythmes (tableau 4.1).

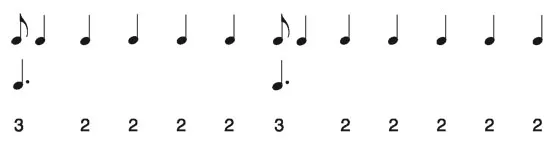
Figure 4.2 – Partie jouée par des lames entrechoquées de machettes en fer.

Tableau 4.1. Inventaire des rythmes asymétriques avec deux durées de trois unités

3 3 2	Zandé
3 2 3 2 2	Aka, Gbaya, Nzakara
3 2 2 3 2 2 2	Gbaya, Ngbaka
3 2 2 2 3 2 2 2 2	non utilisé
3 2 2 2 2 3 2 2 2 2 2	Aka

Le modèle observé chez les Pygmées Aka comporte quatre durées de deux unités d’un côté et cinq de l’autre. Dans la musique de harpe des Nzakara de République centrafricaine, qui sera étudiée au chapitre suivant, les formules de la catégorie gitangi sont fondées sur une cellule rythmique du même type, dont les durées de deux unités sont réparties en deux séries comportant un et deux éléments respectivement. On trouve ce modèle également chez les Pygmées Aka, et chez les Gbaya du nord-ouest de la République centrafricaine. Comme précédemment, les durées de deux unités sont placées de telle sorte qu’il y en a une de plus d’un côté que de l’autre, en constituant deux séries inégales. Simha Arom a également observé un autre rythme appartenant à la même famille chez les Zandé, dans la danse du kponingbo, le grand xylophone posé sur troncs de bananiers. Enfin, on trouve un quatrième modèle présent à la fois chez les Gbaya, et dans un répertoire de harpe des Ngbaka72.

Figure 4.3 – Notation solfégique des rythmes avec deux durées de trois unités et pulsation associée.

Le tableau 4.1 fait apparaître une construction régulière, en forme de pyramide, avec une colonne de trois et une diagonale de trois qui descend vers la droite. Mais on constate une anomalie due au fait que l’une des formules n’est pas utilisée. Pourquoi en effet ne t...

Table des matières

• Couverture
• Titre
• Copyright
• Avant-propos
• Chapitre premier - Mathématiques sans écriture ?
• Chapitre 2 - Arts visuels
• Chapitre 3 - Jeux de stratégie
• Chapitre 4 - Musique (1) : rythmes asymétriques
• Chapitre 5 - Musique (2) : formules de harpe en canon
• Chapitre 6 - Divination (1) : règles de la géomancie
• Chapitre 7 - Divination (2) : cognition
• Conclusion
• Notes
• Index