Groups of Prime Power Order. Volume 4

Yakov G. Berkovich, Zvonimir Janko

• Éditeur: De Gruyter
• Année: 2015
• ISBN:
  9783110381559
• Édition: 1
• Sujet: Mathematics
• Sous-sujet: Group Theory

This is the fourth volume of a comprehensive and elementary treatment of finite p-group theory. As in the previous volumes, minimal nonabelian p- groups play an important role. Topics covered in this volume include:

• subgroup structure of metacyclic p- groups
• Ishikawa's theorem on p- groups with two sizes of conjugate classes
• p- central p- groups
• theorem of Kegel on nilpotence of H p -groups
• partitions of p- groups
• characterizations of Dedekindian groups
• norm of p- groups
• p- groups with 2-uniserial subgroups of small order

The book also contains hundreds of original exercises and solutions and a comprehensive list of more than 500 open problems. This work is suitable for researchers and graduate students with a modest background in algebra.

§ 159 2-groups all of whose cyclic subgroups A, B with A η B = {1} generate an abelian subgroup

This and the following section were written by the second author. These sections contain the solution to Problem 2916.

Heng Lv, Wei Zhou and Dapeng Yu (see [LZY]) have been studying p-groups G all of whose cyclic subgroups are of index at most p2 in their normal closure in G. The main obstacle in these investigations has been two-generator subgroups {x, y} (x, y e G) such that 〈x〉 η 〈y〉 = {1} (see Lemma 144.4 and Lemma 144.5).

On the other hand, if G is a noncyclic p-group such that any two distinct maximal cyclic subgroups of G have intersection equal {1}, then we have either exp(G)= p or G = D2n, n > 3 (see Exercise 12 in Appendix 45). In fact, it is easy to prove this statement. Assume that exp(G) > p and let L G be a maximal cyclic subgroup of order > p. Let L M G with |M : L|= p. By Theorem 1.2, we get p = 2 and M is dihedral. Thus, all subgroups of G containing L and having order 2|L| are dihedral. Suppose that M G. Then N = NG(M) > M and N normalizes L. Let L0 be the cyclic subgroup of order 4 in L so that C = CN(L0) covers N/M, which gives C > L.Let K/L be a subgroup of order 2 in C/L. But then K is not dihedral, a contradiction. Hence we have M = G = D2n, n > 3, and we are done.

Therefore, it is of interest to classify p-groups G such that the following condition is satisfied:

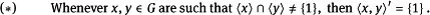
In the first two Propositions 159.1 and 159.2 are determined p-groups G satisfying the condition (*), where G is either minimal nonabelian or metacyclic and p is any prime. It is clear that the condition (* ) says nothing in the case of p-groups of exponent p. But also in the case of 2-groups of exponent 4, the condition (*) says very little, and we characterize such groups in Theorem 159.3.

We recall that a p-group G is p-central if either p > 2 and Ω1 ( G) Z( G) or p = 2 and Ω2 ( G) Z( G). Also, we recall that a 2-group G is quasidihedral if it has an abelian maximal subgroup A of exponent > 2 and an involution t e G - A, which inverts each element in A.

In what follows G will be a 2-group of exponent > 4 satisfying the condition (*) .In Theorem 159.4 we determine up to isomorphism all such groups G which do not possess a normal elementary abelian subgroup of order 8. In Theorem 159.5 we classify our groups G with the assumption that Ü1(G) Z(G). It turns out that these groups must be 2-central, i.e., we must also have 02(G) Z(G). In Proposition 159.6 it is shown that if 02(G) is abelian, then G is also 2-central. Modular 2-groups (i.e., 2-groups that are D8-free) are classified in Theorem 159.7. Then we consider 2-groups G which do not have D8 as a subgroup or equivalently in which Ü1(G) is elementary abelian but 01(G) Z(G), and we show that such groups are of exponent 4 (Theorem 159.8). Finally, we classify in Theorem 159.9 our groups G in which Ü1(G) is nonabelian (i.e., D8 is a subgroup in G). The sta...