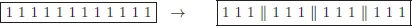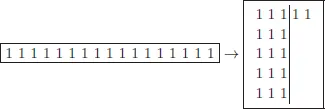Theoretical and Practical Pedagogy of Mathematical Music Theory

Music for Mathematics and Mathematics for Music, From School to Postgraduate Levels

Mariana Montiel, Francisco Gómez

• Éditeur: WSPC
• Année: 2018
• ISBN:
  9789813228368
• Sujet: Mathematics
• Sous-sujet: Mathematics in Education

During the past 40 years, mathematical music theory has grown and developed in both the fields of music and mathematics. In music pedagogy, the need to analyze patterns of modern composition has produced Musical Set Theory, and the use of Group Theory and other modern mathematical structures have become almost as common as the application of mathematics in the fields of engineering or chemistry. Mathematicians have been developing stimulating ideas when exploring mathematical applications to established musical relations. Mathematics students have seen in Music in Mathematics courses, how their accumulated knowledge of abstract ideas can be applied to an important human activity while reinforcing their dexterity in Mathematics. Similarly, new general education courses in Music and Mathematics are being developed and are arising at the university level, as well as for high school and general audiences without requiring a sophisticated background in either music nor mathematics. Mathematical Music Theorists have also been developing exciting, creative courses for high school teachers and students of mathematics. These courses and projects have been implemented in the USA, in China, Ireland, France, Australia, and Spain.

The objective of this volume is to share the motivation and content of some of these exciting, new Mathematical Theory and Music in Mathematics courses while contributing concrete materials to interested readers.

Contents:

• Section I:
  • Rhythm and Transformation (Rachel Hall)
  • Creating a Level Playing Field for Non-music Majors (Timothy A Johnson)
  • Mathematics in Music: An Undergraduate Course (James R Hughes)
  • Phenomenally Loud: Music, Mathematics, and the Diversity of Musical Experience (Jon Kochavi)
• Section II:
  • Mathematical Music Theory: Integrated Course Pairing with Mathematics and Music Students from the USA and China (Mariana Montiel)
  • Scaling Up to Atonality: The Pedagogy of Small Cyclic Universes (Richard Cohn)
• Section III:
  • Matherhythm: Lessons on Divisibility and Rhythm (Francisco Gómez)
  • 'Concerférences': Addressing Different Publics for Mathemusical Popularization (Emmanuel Amiot)
  • Visualizing and Sonifying Mathematical Music Theory with Software Applications: Implications of Computer-Based Models for Practice and Education (Courtney Hilton, Andrea Calilhanna and Andrew J Milne)
  • Muthsics for Clueless: An Experiment with Euclidean Rhythms (Miguel R Wilhelmi and Mariana Montiel)
• Section IV:
  • Can Mathematical Theory of Music Be Easily Learnt and Also Be Fun? (Maria Mannone)

Readership: Students, teachers, researchers. Also a library reference.
Key Features:

• Material on this topic is rare and scattered
• The contributors to this volume are prominent
• The book really intends to be of practical application to instructors with hands-on approach

Section III

Chapter 7

Matherhythm: Lessons on Divisibility and Rhythm

Francisco Gómez

Department of Applied Mathematics, Technical University of Madrid, carretera de Valencia, km. 7, s/n, 28031, Madrid, Spain
[email protected]

7.1.The Divide

Arts and humanities along with sciences are said to be the two faces of the same coin: culture. We strongly disagree; the image of a coin suggests a sharp divide. If we look at one side, we won’t see the other side. The coin itself, when looked at its edge, visually suggests a divide. Instead, we visualize arts, humanities, and sciences all together as a compact, vivid, iridescent ball that, when turned around, shows multiple angles, all of them enriching and complementing each other. However, in society in general and in education in particular, we again encounter a divide. Arts and humanities are sadly and inexplicably separated from science and vice versa. Sciences are taught turning their back on arts and humanities as if their knowledge, methods and open problems couldn’t spark a smidgen of interest, while arts and humanities look at sciences with indifference and incomprehension. Surprisingly enough, the greatest artists, humanity authors and scholars, and scientists deeply appreciate what the other fields of knowledge have to offer. They understand that the more diverse the perspective is, the better the analysis of the subject is. British novelist and scientist Charles Percy Snow condemned the divide between arts and humanities and sciences in a famous 1959 Rede Lecture [14]. The title of the lecture was The Two Cultures and on p. 3 we find one of the most cited paragraphs of his essay.

A good many times I have been present at gatherings of people who, by the standards of the traditional culture, are thought highly educated and who have with considerable gusto been expressing their incredulity at the illiteracy of scientists. Once or twice I have been provoked and have asked the company how many of them could describe the Second Law of Thermodynamics. The response was cold: it was also negative. Yet I was asking something which is the scientific equivalent of: Have you read a work of Shakespeare’s?

I now believe that if I had asked an even simpler question — such as, What do you mean by mass, or acceleration, which is the scientific equivalent of saying, Can you read? — not more than one in ten of the highly educated would have felt that I was speaking the same language. So the great edifice of modern physics goes up, and the majority of the cleverest people in the western world have about as much insight into it as their neolithic ancestors would have had.

How can we then tear down the wall of that divide? The answer presents itself with clarity: through an all-round education. Only education will bring about a sincere and effective change of attitude toward this nefarious divide. Teachers should be the first to change their attitude toward the divide. Unfortunately, a good many science teachers don’t believe arts and humanities have anything of interest to contribute to their lessons, in spite of the many applications of sciences to the domains of arts and humanities (computational linguistics, mathematical sociology, mathematical models in criminal justice, algorithmic art). A good many arts and humanities teachers hold the same beliefs about science, again regardless of the inspiration arts and humanities have drawn from sciences, the use of the same set of higher order thinking skills, or the tools that sciences have built to solve some of their problems.

However, often the problem is not that teachers of both sides don’t desire teaching material inspired in other fields of knowledge. Many do, many crave for it, but they don’t always have the appropriate material available to them. Certainly, most text books and manuals don’t make connections to other disciplines, especially if the content is presented in a traditional way or is oriented to train the student to pass an exam. The aim of this volume is to provide teachers with material of quality to encourage them to teach lessons imbued with knowledge from other fields. Specifically, in this chapter we will establish connections between mathematics and music, more specifically between number theory (theory of division and modular arithmetic) and music theory (theory of rhythm). We will provide the reader with material to prepare a lesson that intertwines math and music. In terms of level the lesson ranges from high school students to college students.

7.2.Matherhythm or Rhythm is a Killer

The lesson we present here is based on the mathematical, musical show that Giovanna Farigu, Gutxi Céspedes and the author of these notes did for the event Maths Week Ireland [4]. This event is a celebration of math, where it is sought to promote awareness, appreciation and understanding of maths through a huge variety of activities. Many of these activities include connections to other fields; for example, they organize mathematical activities involving art, music, juggling, magic, or literature, among others, and bring the best math popularizers such as Andrew Jeffrey [10], Steve Humble [9] (the famous Doctor Math), Colm Mulcahy [12], Fernando Blasco [3], Colin Wright [15] or Kjartan Poskitt [13]. Our show is called Matherhythm [7] and it is a mixture of a serious conference, physical humor, and a music show; it is close to the concept of concerférences developed by Emmanuel Amiot in Chapter 8 of this volume.

We have two versions of the show. The simplest version is just the show suited to a general audience. This version requires the audience to be familiar with the concepts of division and greatest common divisor, although the content of the show is quite self-contained. The other version consists of a show plus a workshop and is suited to work with high school and college students. On some occasions, we give the teachers material to work with the students before the day of the show. On other occasions, we don’t give previous information and after the show a workshop is held; in it, the ideas put forward during the show are explored. These explorations combine math and music activities and finishes by having the students composing music that Giovanna and myself play for them. All these ideas are developed in the next few sections.

The three next sections (Sections 7.3–7.5) contained the lesson. It is structured as follows: the first part is the mathematical section, where the concepts of division and greatest common divisor are introduced as well as Euclid’s algorithm. The second part is the musical part and there a few basic rhythm concepts, such as time span or rhythm, are introduced. In the last part, the matherhythm part, math and music are combined by applying Euclid’s algorithm to the formation of rhythms. The material will be unfolded as it were the script of the show, although not in the form of a dialogue. The exercises associated to each section are shown just right after it. They are presented in increasing order of difficulty so that the last few exercises can be left out for high school audiences. These exercises constitute the material for the workshop.

7.3.The Mathematics

7.3.1.Division

This is a talk about mathematics and music, and in particular, about rhythm. It’s made up of three sections; the first is about mathematics, the second about music, and in the third we’ll mix both. Let’s see, do you all know how to divide? [The audience do.]

We will start by reviewing the concept of division. Division consists of forming groups. In a division you are given two terms, the dividend and the divisor. Thus, dividing the dividend by the divisor is to see how many groups of the size of the divisor can be formed with the dividend. Division is a way of grouping objects. For example, if we have 12 as dividend and 3 as divisor, the division 12÷3 is equivalent to find how many groups of size 3 can be formed with 12 objects (see Fig. 7.1). In this case, the answer is 4. The number of groups is called the quotient. This kind of division is called exact division.

Fig. 7.1.Exact division as formation of groups.

Fig. 7.2.Division with remainder as formation of groups.

Is this clear to you? [The audience give an affirmative nod.]

However, sometimes it is not possible to form an integer numbe...