Inferences in Statistics

12 Key excerpts on "Inferences in Statistics"

• 

  eBook - PDF

  Design and Analysis of Experiments

  Classical and Regression Approaches with SAS

  • Leonard C. Onyiah(Author)
  • 2008(Publication Date)
  • Chapman and Hall/CRC

    (Publisher)

  Chapter 1 Introductory Statistical Inference and Regression Analysis 1.1 Elementary Statistical Inference Generally, when statisticians try to draw some conclusions about a pop-ulation of interest, it is often cheaper and more convenient to draw these conclusions using a sample drawn from the population. Some of the samples used may arise from experiments that are deliberately planned and executed to elicit information of interest. Others may arise from pure observational stud-ies in which the statistician does not control the process but simply observes the responses of the process. Statistical inference, a major area of statisti-cal endeavor, is built around a practical way of obtaining information about populations, namely, sampling. One of the problems commonly dealt with in inferential statistics is the estimation of population values called parameters. A statistic can be used to estimate parameters like mean, median, and vari-ance of a population. Population proportions and the r th moments about the mean are also examples of parameters. Population . The entire collection of attributes that are under study is called a population. The attributes may refer to characteristics of objects such as pencils, steel rods, cars, etc. They may also refer to characteristics of human or animal subjects. Sample . The subset of the population that is used in the actual study is called a sample. Statistical inference . The general field of statistical endeavor that uses sam-ples and sample characteristics to make decisions (make inference) about populations and population characteristics is called statistical inference. Statistic . A value derived from a sample is called a statistic. For clarity, we distinguish between an estimator and an estimate. If we wish to estimate θ , the mean of the normal distribution, it is known that by max-imum likelihood estimation (see Hogg and Craig, 1978, p. 202), the solution 1

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Statistics

  Principles and Methods

  • Richard A. Johnson, Gouri K. Bhattacharyya(Authors)
  • 2019(Publication Date)
  • Wiley

    (Publisher)

  8 Drawing Inferences from Large Samples 1 Two Types of Statistical Inference: Estimation and Testing 2 Point Estimation of a Population Mean 3 Confidence Interval Estimation of a Population Mean 4 Testing Hypotheses About a Population Mean 5 Inferences About a Population Proportion © Markus Mainka/Shutterstock About 50% of working adults are satisfied with their present job. Building Strong Evidence from Diverse Individual Cases One of the major contributions of statistics to modern thinking is the understanding that infor- mation on single, highly variable observations can be combined in great numbers to obtain very precise information about a population. 236 CHAPTER 8/DRAWING INFERENCES FROM LARGE SAMPLES Although each individual is satisfied or not satisfied with his or her job, a sample survey can obtain accurate information about the population proportion that is satisfied. Inferences are generalizations about a population that are made on the basis of a sample collected from the population. For instance, a researcher interested in the growth of pine trees plants 40 seedlings. The heights of these 40 plants would be a sample that is hopefully representative of the population consisting of all current and future seedlings that could be planted. More specifically, we begin by modeling the population by a probability distribution which has a numerical feature of interest called a parameter. A random sample from the population distribution provides information about the parameter. The problem of statistical inference arises when we wish to make generalizations about a population when only a sample is available. Once a sample is observed, its main features can be determined by the methods of descriptive summary discussed in Chapters 2 and 3. However, more often than not, our principal concern is with not just the particular data set, but what can be said about the population based on the information extracted from analyzing the sample data.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  The Fundamentals of Political Science Research

  • Paul M. Kellstedt, Guy D. Whitten(Authors)
  • 2018(Publication Date)
  • Cambridge University Press

    (Publisher)

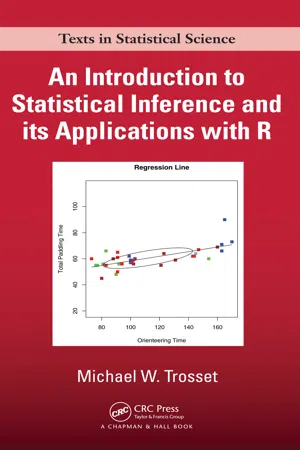
  They revealed some information, but you had to fill in the gaps to draw the conclusion. So when your friend “implies” something, in order to fill in those gaps of understanding, you have to “infer” the rest. Think about how this applies to the concept that we’ve just defined above – “statistical inference.” There are implications for using sample data to learn about a popula- tion. First and foremost is that this process of statistical inference involves, by definition, some degree of uncertainty. That notion, we hope, is rela- tively straightforward: Any time that we wish to learn something general based on something specific, we are going to encounter some degree of uncertainty. For example, if we want to learn about an entire country’s voting-age population, but we don’t have the time or resources to inter- view every member of the voting-age population in that country, we can still learn something about what the population thinks based upon the observations of a sample of that population, provided that we know things about how that sample was selected, and provided that we recognize the uncertainty inherent in extrapolating what we know for sure about our sample to what is likely to be true about the population writ large. In this chapter, we discuss this process of statistical inference, includ- ing the tools that social scientists use to learn about the population that they are interested in by using samples of data. Our first step in this process is to discuss the basics of probability theory, which, in turn, forms the basis for all of statistical inference. 7.2 SOME BASICS OF PROBABILITY THEORY Let’s start with an example. Suppose that you take an empty pillowcase, and that, without anyone else looking, you meticulously count out 550 small blue beads, and 450 small red beads, and place all 1000 of them into the pillowcase. You twist the pillowcase opening a few times to close it up, and then give it a robust shake to mix up the beads.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  An Introduction to Statistical Inference and Its Applications with R

  • Michael W. Trosset(Author)
  • 2009(Publication Date)
  • CRC Press

    (Publisher)

  Chapter 9 Inference Given a specific probability distribution, we can calculate the probabilities of various events. For example, knowing that Y ∼ Binomial( n = 100; p = 0 . 5), we can calculate P (40 ≤ Y ≤ 60). Roughly speaking, statistics is con-cerned with the opposite sort of problem. For example, knowing that Y ∼ Binomial( n = 100; p ), where the value of p is unknown , and having observed Y = y (say y = 32), what can we say about p ? The phrase sta-tistical inference describes any procedure for extracting information about a probability distribution from an observed sample. The present chapter introduces fundamental principles of statistical in-ference. We will discuss three types of statistical inference—point estima-tion, hypothesis testing, and set estimation—in the context of drawing in-ferences about a single population mean. More precisely, we will consider the following situation: 1. X 1 , . . . , X n are independent and identically distributed random vari-ables. We observe a sample, x = { x 1 , . . . , x n } . 2. Both EX i = μ and Var X i = σ 2 exist and are finite. We are interested in drawing inferences about the population mean μ , a quantity that is fixed but unknown. 3. The sample size, n , is sufficiently large that we can use the normal approximation provided by the Central Limit Theorem. We begin, in Section 9.1, by examining a narrative that is sufficiently nuanced to motivate each type of inferential technique. We then proceed to discuss point estimation (Section 9.2), hypothesis testing (Sections 9.3 and 9.4), and set estimation (Section 9.5). Although we are concerned exclusively 197 198 CHAPTER 9. INFERENCE with large-sample inferences about a single population mean, it should be appreciated that this concern often arises in practice. More importantly, the fundamental concepts that we introduce in this context are common to virtually all problems that involve statistical inference.

  Sign up to read

  Learn more about book
• 

  No longer available |Learn more

  Introductory Linear Models & Key Concepts in Statistics and Mathematics

  • (Author)
  • 2014(Publication Date)
  • Orange Apple

    (Publisher)

  ________________________ WORLD TECHNOLOGIES ________________________ Chapter- 4 Statistical Inference Statistical inference is the process of drawing conclusions from data that are subject to random variation, for example, observational errors or sampling variation. More substantially, the terms statistical inference , statistical induction and inferential statistics are used to describe systems of procedures that can be used to draw conclusions from datasets arising from systems affected by random variation. Initial requirements of such a system of procedures for inference and induction are that the system should produce reasonable answers when applied to well-defined situations and that it should be general enough to be applied across a range of situations. The outcome of statistical inference may be an answer to the question what should be done next?, where this might be a decision about making further experiments or surveys, or about drawing a conclusion before implementing some organizational or governmental policy. Introduction Scope For the most part, statistical inference makes propositions about populations, using data drawn from the population of interest via some form of random sampling. More generally, data about a random process is obtained from its observed behavior during a finite period of time. Given a parameter or hypothesis about which one wishes to make inference, statistical inference most often uses: • a statistical model of the random process that is supposed to generate the data, and • a particular realization of the random process; i.e., a set of data. The conclusion of a statistical inference is a statistical proposition. Some common forms of statistical proposition are: • an estimate; i.e., a particular value that best approximates some parameter of interest, • a confidence interval (or set estimate); i.e., an interval constructed from the data in such a way that, under repeated sampling of datasets, such intervals would

  Sign up to read

  Learn more about book
• 

  eBook - ePub

  Easy Interpretation of Biostatistics E-Book

  Easy Interpretation of Biostatistics E-Book

  • Gail F. Dawson(Author)
  • 2012(Publication Date)
  • Saunders

    (Publisher)

  PART II Understanding Inference Passage contains an image Introduction to Understanding Inference

  The ability to define what may happen in the future and to choose among alternatives lies at the heart of contemporary society

  — Peter L. Bernstein 1

  Passage contains an image INTRODUCTION TO PART II

  Inferential statistics can tell us, with a certain degree of confidence, if there is a true difference between two pathways, or if the difference is likely due to chance outcomes. It’s also used to determine the likelihood of a true relationship between two or more variables. We use a sample to represent the population, and only one sample at that. We know that each sample will give a different result, but we are willing to accept a degree of uncertainty so we don’t have to observe each member of the population.

  To illustrate the degree of faith required to accept a result as valid, consider the scenario so eloquently stated by Stanton Glantz in Figure II-1 .

  FIGURE II-1 (A) Results of an experiment in which researchers administered five different doses of a drug to five different people and measured their daily urine production. Output increased as the dose of drug increased in these five people, suggesting that the drug is an effective diuretic in all people similar to those tested. (B) If the researchers had been able to administer the drug to all people and measure their daily urine output, it would have been clear that there is no relationship between the dose of drug and urine output. The five specific individuals who happened to be selected for the study in panel A are shown as shaded points. It is possible, but not likely, to obtain such an unrepresentative sample that leads one to believe that there is a relationship between the two variables when there is none. A set of statistical procedures called tests of hypotheses permits one to estimate the chance of getting such an unrepresentative sample.

  (From Glantz, S. A. 1992. Primer of Biostatistics, 3rd ed. New York, NY: McGraw-Hill, pp. 5-6.)

  Sign up to read

  Learn more about book
• 

  eBook - ePub

  Statistics in Kinesiology

  • Joseph P. Weir, William J. Vincent(Authors)
  • 2020(Publication Date)
  • Human Kinetics

    (Publisher)

  CHAPTER 7 FUNDAMENTALS OF STATISTICAL INFERENCE

  A researcher wishes to characterize the vertical jump performance of Division I female collegiate basketball players. However, there are thousands of players and they are geographically dispersed. It is impractical to test the vertical jump of all the players. Instead, the researcher recruits a random sample of players from several Division I schools and measures their vertical jump performance. The researcher can then use the sample data and the tools of statistical inference to estimate the characteristics of the population.

    Predicting Population Parameters Using Statistical Inference

  In many sciences, little research is conducted on entire populations. Often the population is so large that it would be impossible to measure each member. In such cases, the researcher takes a sample of the population and assumes that the sample represents the population and that the sample statistics are indicative of the population parameters. For this assumption to be valid, the sample must be randomly selected. For more information on sampling selection, see chapter 1 . The process of estimating population parameters based on sample statistics is called inferential statistics.

  Earlier we discussed the problem of determining the mean weight of all men at a university. If the population was 100 or fewer men, we could measure all of them, and a sample would not be needed. But if the population of all men in the university was 15,000, it would be too time consuming to measure all of them. So we would take a random sample to estimate the mean of the population.

  The sample size is limited by such factors as time constraints, finances, facilities, and equipment. If we wanted to measure height or weight, a large sample could be collected because it is easy to measure these variables. But if we were interested in hydrostatically measured body composition or O2

  Sign up to read

  Learn more about book
• 

  eBook - ePub

  Understanding Statistics

  • Bruce J. Chalmer(Author)
  • 2020(Publication Date)
  • CRC Press

    (Publisher)

  The first task for which we use statistical inference is to make statements about parameters using statistics. Of course, if we have access to data for the entire population, no inference is needed; we can simply calculate the parameters in which we are interested. But usually, we must use sample statistics to help us make statements about population parameters. These statements can be of several types.

  Estimation and hypothesis testing

  One type of statement about a parameter is simply to estimate its value. An estimate can be a point estimate, meaning a single value, or an interval estimate, meaning a range of values. For example, we might estimate that the number of people who will die in traffic accidents over a certain weekend will be 450 (a point estimate), or we might estimate the number to be between 430 and 470 (an interval estimate).

  Another type of statement about a parameter derives from a procedure called hypothesis testing. Hypothesis testing is related to estimation, but the emphasis is different. For example, we might wish to determine whether there is any difference in average amount of pain reported after oral surgery between people taking a drug and people receiving a placebo (a substance that has no inherent effect on pain). We are looking for statistical evidence that the drug has some effect on pain beyond the placebo effect. (Curiously, many studies have shown that about a third of people who receive placebos derive considerable pain relief.) The emphasis is not on estimating the degree of difference between drug and placebo, but simply on testing whether there is a difference.

  Determining degree of certainty

  The second task for which we use statistical inference is to determine how certain we are that our statements are true. It may seem odd to make statements if we are not sure they are true. (Actually, the odd part is admitting it!) But as we noted in Chapter 1

  Sign up to read

  Learn more about book
• 

  eBook - ePub

  Mathematics for Biological Scientists

  • Mike Aitken, Bill Broadhurst, Stephen Hladky(Authors)
  • 2009(Publication Date)
  • Garland Science

    (Publisher)

  In Chapter 9 we saw how to describe the numbers in a sample. What we would like to do now is to use this sample to draw conclusions about the population of ‘all possible measurements’. The aim of inferential statistics is therefore to draw conclusions about the possible values of the population properties (parameters) that might plausibly have given us our sample properties (statistics). The techniques that help us to make decisions based upon estimates of the parameters of the underlying population are called parametric techniques. There are other techniques, known as non-parametric techniques, that try to help us make inferences when we cannot estimate these parameters (for example, if we cannot treat our data as interval data, and thus cannot calculate a sample mean). Before we go on, it is worth stopping to make a point about notation. There is a simple convention that is followed throughout almost all disciplines in science and mathematics: population parameters (that we are estimating, or drawing conclusions about) are written as Greek characters (such as σ 2 for a variance, and π for a proportion). Sample statistics (that we calculate directly from experimental data) are written as roman (ordinary alphabet) characters (such as s 2 for a sample variance, and p for a proportion). Box 11.1 Notation for sample and population statistics We need to distinguish between the descriptive statistics that characterize our sample (which we know), and the corresponding parameters that characterize the population (to which we wish to generalize)

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Applied Statistics for Public and Nonprofit Administration

  • Kenneth Meier, Jeffrey Brudney, John Bohte, , Kenneth Meier, Jeffrey Brudney, John Bohte(Authors)
  • 2014(Publication Date)
  • Cengage Learning EMEA

    (Publisher)

  Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. 167 CHAPTER 10 W hen statistics are used to summarize the distribution of a given sample or population, we call this summarizing descriptive statistics . In descriptive statistics, we use statistical techniques to describe and summarize data. Inferential statistics is the use of quantitative techniques to generalize from a sample to a population. In short, with inferential statistics, we hope to use a small subset or sample of data to infer what all the data or the population look like. For example, the city officials in Pittsburgh, Pennsylvania, would like to know how pleased Pittsburgh citizens are with their new bus service. The best way to do this would be to ask every citizen of Pittsburgh how he or she feels about the transit system. Because the population of Pittsburgh is about 350,000 people, this interviewing could take forever (not to mention that it would cost more to do that than to run the transit system). An alternative is to randomly select a subset of persons (say, 100) and ask them about the mass transit system. From this sample, we will infer what the people of Pittsburgh think. In this chapter, we begin the presentation of inferential statistics by reviewing some basic definitions and describing some simple inferential techniques. Some Definitions A population is the total set of items that we are concerned about. In the preced-ing example, the population is all the people who live in Pittsburgh, Pennsylvania. A measure that is used to summarize a population is called a parameter . For example, the mean education level in Pittsburgh is 12.9 years.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Statistics

  Unlocking the Power of Data

  • Robin H. Lock, Patti Frazer Lock, Kari Lock Morgan, Eric F. Lock, Dennis F. Lock(Authors)
  • 2020(Publication Date)
  • Wiley

    (Publisher)

  196 C H A P T E R 3 Confidence Intervals 3.1 SAMPLING DISTRIBUTIONS In Chapter 1 we discuss data collection: methods for obtaining sample data from a population of interest. In this chapter we begin the process of going in the other direc- tion: using the information in the sample to understand what might be true about the entire population. If all we see are the data in the sample, what conclusions can we draw about the population? How sure are we about the accuracy of those conclu- sions? Recall from Chapter 1 that this process is known as statistical inference. Statistical Inference Statistical inference is the process of drawing conclusions about the entire population based on the information in a sample. Data Collection Statistical Inference Population Sample Statistical inference uses sample data to understand a population Population Parameters and Sample Statistics To help identify whether we are working with the entire population or just a sample, we use the term parameter to identify a quantity measured for the population and statistic for a quantity measured for a sample. Parameters vs Statistics A parameter is a number that describes some aspect of a population. A statistic is a number that is computed from the data in a sample. As we saw in Chapter 2, although the name (such as “mean” or “proportion”) for a statistic and parameter is generally the same, we often use different notation to distinguish the two. For example, we use  (mu) as a parameter to denote the mean for a population and x as a statistic for the mean of a sample. Table 3.1 summarizes Table 3.1 Notation for common parameters and statistics Population Parameter Sample Statistic Mean  x Standard deviation  s Proportion p  p Correlation  r Slope (regression)  b 3.1 Sampling Distributions 197 common notation for some population parameters and corresponding sample statis- tics. The notation for each should look familiar from Chapter 2.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Statistics for Business and Economics

  • Carlos Cortinhas, Ken Black(Authors)
  • 2014(Publication Date)
  • Wiley

    (Publisher)

  38–45; and ‘Word- of-Mouth Advertising’, Entrepreneur magazine, 2009, available at: www .entrepreneur.com/encyclopedia/term/82660. html. A foremost statistical mechanism for decision making is the hypothesis test. The concept of hypothesis testing lies at the heart of inferential sta- tistics, and the use of statistics to ‘prove’ or ‘disprove’ claims hinges on it. With hypothesis testing, business researchers are able to structure problems in such a way that they can use statistical evidence to test vari- ous theories about business phenomena. Business applications of statistical hypothesis testing run the gamut from determining whether a production line process is out of control to providing conclusive evidence that a new management leadership approach is significantly more effective than an old one. Figure III-1 in the Unit III Introduction displays a tree diagram taxonomy of inferential techniques, organizing them by usage, number of samples, and type of statistic. While Chapter 8 contains the portion of these techniques that can be used for estimating a mean, a proportion, or a variance for a population with a single sample, Chapter 9 contains techniques used for testing hypotheses about a population mean, a population proportion, and a population variance using a single sample. The entire right side of the tree diagram taxonomy displays various hypothesis-testing techniques. The leftmost branch of this right side contains Chapter 9 techniques (for single samples), and this branch is displayed in Figure 9.1. Note that at the bottom of each tree branch in Figure 9.1, the title of the statistical technique along with its respective section number is given for ease of identification and use. If a business researcher is testing a population mean and the population standard deviation is known, then she will use the z test for  contained in Section 9.2.

  Sign up to read

  Learn more about book