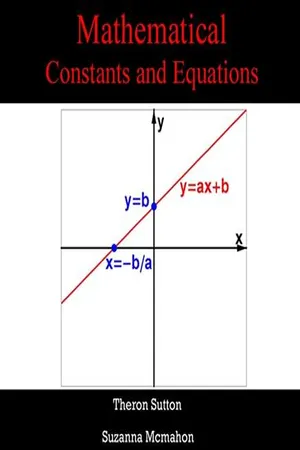
Mathematics
Multiples of Pi
Multiples of Pi refer to any number that is a multiple of the mathematical constant Pi (π). Pi is the ratio of the circumference of a circle to its diameter and is approximately equal to 3.14159. Multiples of Pi are commonly used in trigonometry and other mathematical calculations.
Written by Perlego with AI-assistance
Related key terms
1 of 5
8 Key excerpts on "Multiples of Pi"
- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Orange Apple(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter- 3 Pi ( π ) Mosaic depicting π at the entrance to the math building at Technische Universität Berlin π (sometimes written pi ) is a mathematical constant whose value is the ratio of any Euclidean plane circle's circumference to its diameter; this is the same value as the ratio of a circle's area to the square of its radius. It is approximately equal to 3.14159265 in the usual decimal notation. Many formulae from mathematics, science, and engineering involve π, which makes it one of the most important mathematic al constants. π is an irrational number, which means that its value cannot be expressed exactly as a fraction m / n , where m and n are integers. Consequently, its decimal representation never ________________________ WORLD TECHNOLOGIES ________________________ ends or repeats. It is also a transcendental number, which implies, among other things, that no finite sequence of algebraic operations on integers (powers, roots, sums, etc.) can be equal to its value; proving this was a late achievement in mathematical history and a significant result of 19th century German mathematics . Throughout the history of mathematics, there has been much effort to dete rmine π more accurately and to understand its nature; fascination with the number has even carried over into non-mathematical culture. Probably because of the simplicity of its definition, the concept of π has become entrenched in popular culture to a degree far greater than almost any other mathematical construct. It is, perhaps, the most common ground between mathematicians and non-mathematicians. Reports on the latest, most-precise calculation of π are common news items. The current record for the decimal expansion of π, if verified, stands at 5 trillion digits. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 3 Pi ( π ) Mosaic depicting π at the entrance to the math building at Technische Universität Berlin π (sometimes written pi ) is a mathematical constant whose value is the ratio of any Euclidean plane circle's circumference to its diameter; this is the same value as the ratio of a circle's area to the square of its radius. It is approximately equal to 3.14159265 in the usual decimal notation. Many formulae from mathematics, science, and engineering involve π, which makes it one of the most important mathematica l constants. π is an irrational number, which means that its value cannot be expressed exactly as a fraction m/n, where m and n are integers. Consequently, its decimal representation never ends or repeats. It is also a transcendental number, which implies, among other things, that no finite sequence of algebraic operations on integers (powers, roots, sums, etc.) can ________________________ WORLD TECHNOLOGIES ________________________ be equal to its value; proving this was a late achievement in mathematical history and a significant result of 19th century German ma thematics. Throughout the history of mathematics, there has been much effort to dete rmine π more accurately and to under -stand its nature; fascination with the number has even carried over into non-mathematical culture. Probably because of the simplicity of its definition, the concept of π has become entr -enched in popular culture to a degree far greater than almost any other mathematical construct. It is, perhaps, the most common ground between mathematicians and non-mathematicians. Reports on the latest, most-precise calculation of π are common news items. The current record for the decimal expansion of π, if verified, stands at 5 trillion digits. - eBook - ePub
Mathematica Beyond Mathematics
The Wolfram Language in the Real World
- José Guillermo Sánchez León(Author)
- 2022(Publication Date)
- Chapman and Hall/CRC(Publisher)
7 Calculating π and Other Mathematical TalesThe first six sections of this chapter are dedicated to π, one of the most famous mathematical constants. What looks like a simple geometric ratio between the length of a circle's circumference and its diameter has surprising properties and unexpected connections to seemingly unrelated fields. Many famous mathematicians throughout history have created their own formulas to calculate the largest number of decimals of π in the most efficient possible way, something that they currently still do. The last two sections discuss the Riemann hypothesis, one of the most important unsolved problems in mathematics, and its connection to the prime numbers.7.1 The Origins of π
Approximately 4,000 years ago, Egyptians and Babylonians already knew that the ratio between the circle's circumference and its diameter, what we call π (pi) nowadays, had a constant value slightly higher than 3.The first estimates were most likely based on experimental measurements. After drawing a circle and measuring its perimeter and diameter, you will notice that the perimeter is a bit more than three times the diameter.The Old Testament includes an estimation of π in the First Book of Kings 7:23, referring to the construction of Solomon's temple. We can read: “And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it round about”; that is, its circumference was 30 cubits and its diameter was 10 cubits, so the relationship between the circumference and the diameter is 3.In the Great Pyramid of Giza there are ratios clearly showing that the Egyptians had obtained a good approximation to the value of ℼ. The Rhind Papyrus (circa 1650 B.C.), one of the best sources about mathematics in Ancient Egypt, contains the following ratio as the value of ℼ:256 81= 3.16049 - eBook - ePub
Here's Looking at Euclid
A Surprising Excursion Through the Astonishing World of Math
- Alex Bellos(Author)
- 2010(Publication Date)
- Free Press(Publisher)
A century before Klein, another human calculator, Johann Zacharias Dase, was also employed by the scientific establishment, to do their sums for them. Dase was born in Hamburg and started performing as a lightning calculator in his teens, when he was taken under the wing of two eminent mathematicians. In the days before electronic or mechanical calculators, scientists relied on logarithm tables to do complicated multiplications and divisions. As I will explain in more detail in the next chapter, every number has its own logarithm, which can be calculated using a laborious procedure of adding fractions. Dase calculated the natural logarithms of the first 1,005,000 numbers, each to seven decimal places. It took him three years, and he said he enjoyed the task. Then, on the recommendation of the mathematician Carl Friedrich Gauss, Dase embarked on another enormous project: compiling a table of factors of all the numbers between 7,000,000 and 10,000,000. This means he looked at every number in the range and calculated its factors, which are the whole numbers that divide that number. For example, 7,877,433 has only two factors: 3 and 2,625,811. When Dase died, age 37, he had completed a substantial part of this project.Yet it was another calculation for which Dase is best remembered. When he was still a teenager he calculated pi to 200 places, a record for the time.Circles are everywhere in the natural world—you see them in the silhouette of the moon, in the eyes of humans and animals and in the cross section of an egg. Tie a dog to a post and the path it patrols when the lead is taut is a circle. The circle is the simplest two-dimensional geometrical shape. An Egyptian farmer counting up how much of a crop to plant in a round field, or a Roman mechanic measuring the length of wood for a wheel, would have needed to make calculations involving circles.The ancient civilizations realized that the ratio of the circle’s circumference to its diameter was always the same, no matter how big or small you made the circle. (The circumference is the distance around a circle, and the diameter is the distance across through the center.) The ratio is known as pi and it works out as just over three. So, if you take the diameter of a circle and curve it around the circumference, you will find that it fits just over three times.Even though pi is a simple ratio between properties of a circle, the task of finding its exact value has proved to be far from simple. This elusiveness has made pi an object of fascination for thousands of years. It is the only number that is both the name of a song by Kate Bush and a fragrance by Givenchy, whose PR department sent me the following text:π – PiBEYOND INFINITY Four thousand years have passed and the mystery remains. Although every schoolchild studies π, the familiar symbol still manages to hide an abyss of great complexity. - eBook - PDF
Dr. Math Introduces Geometry
Learning Geometry is Easy! Just ask Dr. Math!
- (Author)
- 2004(Publication Date)
- Jossey-Bass(Publisher)
So if pi were written in binary, it would appear to have just ones and zeros also. —Dr. Math, The Math Forum Circles and Pi 103 BUFFON’S NEEDLE EXPERIMENT If you throw n needles, each of which is length 1, at a floor with horizontal stripes every 1 unit, the ratio of needles that cross a stripe to the total number of needles will approach 2/π as you have more and more needles. This can be a fun classroom experiment. 104 Dr. Math Introduces Geometry R esources on the Web Learn more about circles at these sites: Math Forum: Designs with Circles—Suzanne Alejandre mathforum.org/alejandre/circles.html Students can read about circles in Islamic cultures and explore the geometry involved in circle designs. Math Forum: The Derivation of Pi mathforum.org/te/exchange/hosted/basden/pi_3_14159265358.html Students use real-world objects to understand the concept of a con- stant such as pi. Math Forum: Pi Day Songs mathforum.org/te/exchange/hosted/morehouse/songs.pi.html Songs to sing as part of a Pi Day celebration. Math Forum: The Pi Trivia Quiz mathforum.org/te/exchange/hosted/morehouse/trivia.pi.html Test your trivia knowledge of pi. Math Forum: The Area of a Circle mathforum.org/te/exchange/hosted/basden/circle_area/circle_area. html Students derive the formula for the area of a circle. Shodor Organization: Project Interactivate: Buffon’s Needle shodor.org/interactivate/activities/buffon/ This activity allows the user to run a simulation of dropping a nee- dle on a lined sheet of paper and determining the probability of the needle crossing one of the lines. W e’ve looked a lot so far at one- and two-dimensional objects. In this part we’ll look at three-dimensional objects, or solids. Do you remember how it was useful to know something about lines in order to work with polygons and circles? Well, it’s useful to know things about polygons and circles in order to work with three-dimensional objects. - eBook - PDF
Mathematics by Experiment
Plausible Reasoning in the 21st Century
- Jonathan Borwein, David Bailey(Authors)
- 2008(Publication Date)
- A K Peters/CRC Press(Publisher)
3 Pi and Its Friends I am ashamed to tell you to how many figures I carried these com-putations, having no other business at the time. – Issac Newton, personal journal, 1666 The desire, as well as the need, to calculate ever more accurate values of π , the ratio of the circumference of a circle to its diameter, has challenged mathematicians for many centuries. In recent years, π computations have provided some fascinating examples of computational mathematics. But first, a little historical background, which we have condensed from a 1997 article [23]. Additional historical details are available from the fascinating new book Pi Unleashed [10], and from [49, 74]. We should also mention the MacTutor web site, maintained by the Department of Mathematics at the University of St. Andrews in Scotland: http://www-gap.dcs.st-and .ac.uk/ ∼ history. This is particularly good for biographical information about historical mathematicians, including those involved with π . 3.1 A Short History of Pi About 2000 BCE, the Babylonians used the approximation 3 1 8 = 3 . 125. At this same time or earlier, according to an ancient Egyptian document, Egyptians assumed that a circle with diameter nine has the same area as a square of side eight, which implies π = 256 81 = 3 . 1604 . . . Some have argued from the following biblical passage that the ancient Hebrews used π = 3: Also, he made a molten sea of ten cubits from brim to brim, round in compass, and five cubits the height thereof; and a line of thirty cubits did compass it round about (1 Kings 7:23; see also 2 Chron. 4:2). The first rigorous mathematical calculation of the value of π was due to Archimedes (ca. 250 BCE), who used a scheme based on inscribed and circumscribed polygons to obtain the bounds 3 10 71 < π < 3 1 7 . Indeed, Archimedes’ scheme constitutes the first true algorithm for π , in the sense 103 - eBook - ePub
- Ian Stewart(Author)
- 2013(Publication Date)
- Profile Books(Publisher)
3The puzzle of pi Squaring the CirclePRIMES ARE AN OLD IDEA , but circles are even older. Circles led to a great problem that took more than 2000 years to solve. It is one of several related geometric problems that have come down to us from antiquity. The central character in the story is the number π (Greek ‘pi’) which we meet at school in connection with circles and spheres. Numerically it is 3.14159 and a bit; often the approximation 22/7 is used. The digits of π never stop, and they never repeat the same sequence over and over again. The current record for calculating digits of π is 10 trillion digits, by Alexander Yee and Chigeru Kondo in October 2011.14 Computations like this are significant as ways to test fast computers, or to inspire and test new methods to calculate π, but very little hinges on the numerical results. The reason for being interested in π is not to calculate the circumference of a circle. The same strange number appears all over mathematics, not just in formulas related to circles and spheres, and it leads into very deep waters indeed. The school formulas are important, even so, and they reflect π’s origins in Greek geometry.There, one of the great problems was the unsolved task of squaring the circle. This phrase is often employed colloquially to indicate a wrong-headed approach to something, rather like trying to fit a square peg into a round hole. Like many common phrases extracted from science, this one’s meaning has changed over the centuries.15 In Greek times, trying to square the circle was a perfectly reasonable idea. The difference in the two shapes – straight or curved – is totally irrelevant: similar problems have valid solutions.16 - eBook - ePub
Isotopic Randomness and Self-Organization
In Physics, Biology, Nanotechnology, and Digital Informatics
- Alexander Berezin(Author)
- 2018(Publication Date)
- De Gruyter(Publisher)
π somewhere (and, again, infinitely many times with all possible variations!). Such is the power of infinity!The number π is, of course, a universal constant of mathematics, which can be defined in many ways, not just as the ratio of the length of a circle to its diameter. For example, it can be defined by the infinite Leibniz series. Repeating from Chapter 5 , this series is:(8.2)π / 4= 1 −1 / 3+1 / 5−1 / 7+1 / 9−1 / 11+ …a d i n f i n i t u mThis very simple-looking series, although it converges very slowly (there other serial expansions for π which converge much more quickly, but they are more complicated) does, nonetheless, converge to the exact value of π /4, even if this series as such has (seemingly) no clear relationship to circles.That probably “metaphysically explains” (if such a term can be used) why π is not exactly three. Would it not be nice if it should be so? (except that, perhaps, the Universe would be much more boring). However, π is, and will always be, some strange, irrational, and transcendental (and likely normal) number that places itself somewhere between 3.1 and 3.2. And no talk about “other realities” or “parallel universes” can be entertained here, because in any logically consistent realm, π will be exactly as it is, it is as absolutely eternal and unchangeable as the (infinite) list of Prime Numbers.Thus, asking why π is not exactly three is, perhaps, like asking why there is an infinity of Prime Numbers. In fact, since Prime Numbers become increasingly sparse as we progress along the number line, common sense may tell us that sooner or later the Prime Numbers will run out and there will be no more of them. However, contrary to such common sense, as early as the third century BCE, Euclid gave a neat and clear proof that there is no “largest” Prime Number and there is infinity of them (refer Chapter 3 for Euclid’s proof).The above comments do not, however, derail the idea of “hidden messages” in normal numbers. On the contrary, the situation with hidden messages is, in a sense, even better than in Sagan’s novel. The Platonic world of mathematics is full of them. Furthermore, this idea has enormous constructive power. The fact that real numbers (normal numbers) in their very structure contain an infinite manifold of messages and patterns of all kinds serves as the basis for all the phenomena of emergence and self-organization occurring in the Universe (Berezin, 1998b , 2015 , 2016
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.