Mathematics
Normal Distribution
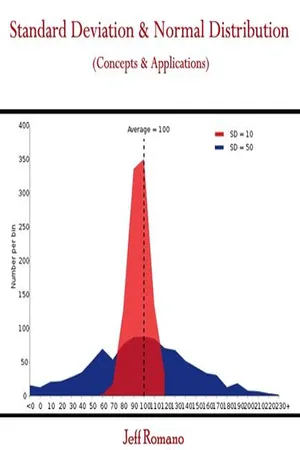
Normal distribution is a probability distribution that is symmetric and bell-shaped. It is characterized by its mean and standard deviation, and many natural phenomena follow this distribution. The majority of the data falls within one standard deviation of the mean, and the probability of extreme values decreases rapidly as they move away from the mean.
Written by Perlego with AI-assistance
Related key terms
1 of 5
12 Key excerpts on "Normal Distribution"
- No longer available |Learn more
- Anthony Hayter(Author)
- 2012(Publication Date)
- Cengage Learning EMEA(Publisher)
C H A P T E R F I V E The Normal Distribution In this chapter the normal or Gaussian distribution is discussed. It is the most important of all continuous probability distributions and is used extensively as the basis for many statistical inference methods. Its importance stems from the fact that it is a natural probability distribution for directly modeling error distributions and many other naturally occurring phenomena. In addition, by virtue of the central limit theorem , which is discussed in Section 5.3, the Normal Distribution provides a useful, simple, and accurate approximation to the distribution of general sample averages. 5.1 Probability Calculations Using the Normal Distribution 5.1.1 Definition of the Normal Distribution The Normal Distribution The normal or Gaussian distribution has a probability density function f ( x ) = 1 σ √ 2 π e − ( x − μ) 2 / 2 σ 2 for −∞ ≤ x ≤ ∞ , depending upon two parameters, the mean and the variance E ( X ) = μ and Var ( X ) = σ 2 of the distribution. The probability density function is a bell-shaped curve that is symmetric about μ . The notation X ∼ N (μ, σ 2 ) denotes that the random variable X has a Normal Distribution with mean μ and variance σ 2 . In addition, the random variable X can be referred to as being “normally distributed.” HISTORICAL NOTE Carl Friedrich Gauss (1777–1855) ranks as one of the greatest mathematicians of all time. He studied mathematics at the University of G¨ ottingen, Germany, between 1795 and 1798 and later in 1807 became professor of astronomy at the same university, where he remained until his death. His work on the Normal Distribution was performed around 1820. He is reported to have been deeply religious, aristocratic, and conservative. He did not enjoy teaching and consequently had only a few students. The probability density function of a normal random variable is symmetric about the mean value μ and has what is known as a “bell-shaped” curve. - eBook - PDF
- Roy E Bruns, Ieda Spacino Scarminio, Benicio de Barros Neto(Authors)
- 2006(Publication Date)
- Elsevier Science(Publisher)
One of the most important statistical models — arguably the most important — is the normal (or Gaussian ) distribution that the famous mathematician Karl F. Gauss proposed at the beginning of the 19th century, to calculate the probabilities of occurrence of measurement When the situation is normal 23 errors. 13 So many data sets were — and still are — well represented by the Normal Distribution that it has come to be considered the natural behavior for any type of experimental error: hence the adjective normal . If on occasion one encountered an error distribution that failed to conform to a Gaussian function, the data collection procedure was usually viewed with suspicion. Later it became clear that many legitimate experimental situations arise for which the Normal Distribution does not apply. Nevertheless, it remains one of the fundamental models of statistics. Many of the results we present later are rigorously valid only for data following a Normal Distribution. In practice this is not so severe a restriction, because almost all the tests we will study remain efficient in the presence of moderate departures from normality, and because we can use adequate experimental planning to reduce the effects of possible non-normalities. 2.3.1. Calculating probabilities of occurrence A statistical distribution is a function that describes the behavior of a random variable, that is, a quantity that can assume any permissible value for the system to which it refers, but for which the chance of occurrence is governed by some probability distribution. If we could discover or estimate the nature of this distribution, we could calculate the probability of occurrence of any value of interest. We would, in fact, possess a sort of statistical crystal ball we could use to make predictions. Soon we will see how to do this using the Normal Distribution. - Rajan Chattamvelli, Ramalingam Shanmugam(Authors)
- 2022(Publication Date)
- Springer(Publisher)
93 C H A P T E R 8 Normal Distribution 8.1 INTRODUCTION The Normal Distribution is perhaps the most widely studied continuous distribution in statistics. It originated in the works of Abraham De Moivre (1733), who derived it as the limiting form of binomial distribution BINO(n,p) as n ! 1 where p remains a constant. It is known by the name Gaussian distribution in engineering in honor of the German mathematician Carl Friedrich Gauss (1777–1855) who applied it to least square estimation technique, and worked extensively with its properties. 1 It has two parameters, which are by convention denoted as and to indicate that they capture the location (mean) and scale information. The PDF is denoted by .xI ; / (and the CDF by ˆ.xI ; /) as .xI ; / D 1 p 2 e 1 2 . x / 2 ; 1 < x < 1; 1 < < 1; > 0: (8.1) The distribution is denoted by N( ; 2 ) where the first parameter is always the population mean, and the second parameter is the population variance. The first parameter should be specified even when the mean is zero. Thus, N(0, 2 ) denotes a Normal Distribution with zero mean. A Gaussian distributed random variable is called a normal deviate. Some authors use the notation N( ; ) where the second parameter is the population standard deviation, and vertical bar (j) instead of semicolon as .xj ; /. It is called a normalized normal, standard normal, standardized normal, or unit Normal Distribution (UND) when the mean is 0 and variance is 1. (Note that the abbreviation SND is used for skew-Normal Distribution discussed in Section 8.5.) The standard normal random variable will be denoted by Z.0; 1/ or Z; its PDF by .z I 0; 1/, .z/, or f .z/; and CDF by ˆ.z I 0; 1/ or ˆ.z/ where z in the CDF is the upper limit of the integral. Any Normal Distribution (with arbitrary and ) can be converted into the standard normal form N(0,1) using the transformation Z D .X /= . This is called “standard nor- malization” as it standardizes the variate X to have zero mean and variance unity.- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Learning Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter- 6 Normal Distribution and Central Limit Theorem Normal Distribution Probability density function The red line is the standard Normal Distribution Cumulative distribution function ________________________ WORLD TECHNOLOGIES ________________________ Colors match the image above notation: parameters: μ ∈ R — mean (location) σ 2 > 0 — variance (squared scale) support: x ∈ R pdf: cdf: mean: μ median: μ mode: μ variance: σ 2 skewness: 0 ex.kurtosis: 0 entropy: mgf: cf: Fisher information: In probability theory, the normal (or Gaussian ) distribution , is a continuous probability distribution that is often used as a first approximation to describe real-valued random variables that tend to cluster around a single mean value. The graph of the associated probability density function is “bell”-shaped, and is known as the Gaussian function or bell curve : where parameter μ is the mean (location of the peak) and σ 2 is the variance (the measure of the width of the distribution). The distribution with μ = 0 and σ 2 = 1 is called the standard normal . The Normal Distribution is considered the most “basic” continuous probability distribution due to its role in the central limit theorem, and is one of the first continuous distributions taught in elementary statistics classes. Specifically, by the central limit theorem, under certain conditions the sum of a number of random variables with finite means and variances approaches a Normal Distribution as the number of variables increases. For this reason, the Normal Distribution is commonly encountered in practice, and is used ________________________ WORLD TECHNOLOGIES ________________________ throughout statistics, natural sciences, and social sciences as a simple model for complex phenomena. - eBook - PDF
- Barbara Illowsky, Susan Dean(Authors)
- 2016(Publication Date)
- Openstax(Publisher)
6 | THE Normal Distribution Figure 6.1 If you ask enough people about their shoe size, you will find that your graphed data is shaped like a bell curve and can be described as normally distributed. (credit: Ömer Ünlϋ) Introduction Chapter Objectives By the end of this chapter, the student should be able to: • Recognize the normal probability distribution and apply it appropriately. • Recognize the standard normal probability distribution and apply it appropriately. • Compare normal probabilities by converting to the standard Normal Distribution. The normal, a continuous distribution, is the most important of all the distributions. It is widely used and even more widely abused. Its graph is bell-shaped. You see the bell curve in almost all disciplines. Some of these include psychology, business, economics, the sciences, nursing, and, of course, mathematics. Some of your instructors may use the Normal Distribution to Chapter 6 | The Normal Distribution 361 help determine your grade. Most IQ scores are normally distributed. Often real-estate prices fit a Normal Distribution. The Normal Distribution is extremely important, but it cannot be applied to everything in the real world. In this chapter, you will study the Normal Distribution, the standard Normal Distribution, and applications associated with them. The Normal Distribution has two parameters (two numerical descriptive measures), the mean (μ) and the standard deviation (σ). If X is a quantity to be measured that has a Normal Distribution with mean (μ) and standard deviation (σ), we designate this by writing Figure 6.2 The probability density function is a rather complicated function. Do not memorize it. It is not necessary. f(x) = 1 σ ⋅ 2 ⋅ π ⋅ e − 1 2 ⋅ ⎛ ⎝ x − µ σ ⎞ ⎠ 2 The cumulative distribution function is P(X < x). It is calculated either by a calculator or a computer, or it is looked up in a table. - Claus Thorn Ekstrom, Helle Sørensen(Authors)
- 2014(Publication Date)
- Chapman and Hall/CRC(Publisher)
Chapter 4 The Normal Distribution Statistical models describe the systematic behavior as well as the random variation in a precise manner. In this chapter we introduce the normal distri-bution as a tool to describe random variation. So far we have focused on the average or expected behavior of the obser-vations. In linear regression, we looked at the expected value of y for a given value of x , and in the one-way ANOVA setting, we modeled the expected value for an observation from group j . The average behavior is described by the systematic (or fixed) part of a model. However, we have also emphasized that there is variation around these expected values — not all y ’s have the same value even though they have the same corresponding value of x (linear regression), and not all observations within a group are identical (one-way ANOVA) — and that we need to take this random variation into account. In situations where the response variable — the variable we wish to make a model for — is continuous, then the Normal Distribution or Gaussian distri-bution is by far the most important distribution for that purpose. The Normal Distribution is not useful for categorical data, and in Chapters 11 and 13 we will work with the binomial distribution for binary data. The Normal Distribution is important for several reasons: First — and for our purpose most important — the Gaussian distribution turns out to de-scribe many types of data very well, not the least biological data. This is partly due to “the central limit theorem” (CLT) stating that averages are ap-proximately normally distributed, (almost) no matter the properties of the original variables (see Section 4.4). Second, the Gaussian distribution has very nice mathematical properties, which makes the analysis exact (not re-lying on approximations) and rather simple. The Gaussian distribution is named after the German mathematician and physicist Carl Friedrich Gauss (1777—1855).- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
From a technical perspective, alternative characterizations are possible, for example: • The Normal Distribution is the only absolutely continuous distribution all of whose cumulants beyond the first two (i.e. other than the mean and variance) are zero. • For a given mean and variance, the corresponding Normal Distribution is the continuous distribution with the maximum entropy. Definition The simplest case of a Normal Distribution is known as the standard Normal Distribution, described by the probability density function The constant in this expression ensures that the total area under the curve ϕ (x) is equal to one, and 1 ⁄ 2 in the exponent makes the “width” of the curve (measured as half of the distance between the inflection points of the curve) also equal to one. It is traditional in statistics to denote this function with the Greek letter ϕ (phi), whereas density functions for all other distributions are usually denoted with letters ƒ or p. The alternative glyph φ is also used quite often, however within this we reserve “ φ ” to denote characteristic functions. More generally, a Normal Distribution results from exponentiating a quadratic function (just as an exponential distribution results from exponentiating a linear function): ________________________ WORLD TECHNOLOGIES ________________________ This yields the classic “bell curve” shape (provided that a < 0 so that the quadratic function is concave). Notice that ƒ(x) > 0 everywhere. One can adjust a to control the “width” of the bell, then adjust b to move the central peak of the bell along the x-axis, and finally adjust c to control the “height” of the bell. For ƒ(x) to be a true probability density function over R , one must choose c such that (which is only possible when a < 0). Rather than using a, b, and c, it is far more common to describe a Normal Distribution by its mean μ = − b/(2a) and variance σ 2 = −1/(2 a). - eBook - PDF
Statistics
Principles and Methods
- Richard A. Johnson, Gouri K. Bhattacharyya(Authors)
- 2019(Publication Date)
- Wiley(Publisher)
Although the normal curve is not unique in exhibiting this form, it has been found to provide a reasonable approximation in a great many situations. Unfortunately, at one time during the early stages of the development of statistics, it had many overzealous admirers. Apparently, they felt that all real-life data must conform to the bell-shaped normal curve, or otherwise, the process of data collection should be suspect. It is in this context that the distribution became known as the Normal Distribution. 2. THE Normal Distribution—ITS GENERAL FEATURES 185 However, scrutiny of data has often revealed inadequacies of the Normal Distribution. In fact, the universality of the Normal Distribution is only a myth, and examples of quite nonNormal Distributions abound in virtually every field of study. Still, the Normal Distribution plays a central role in statistics, and inference procedures derived from it have wide applicability and form the backbone of current methods of statistical analysis. Although we are speaking of the importance of the Normal Distribution, our remarks really apply to a whole class of distributions having bell-shaped densities. There is a Normal Distribution for each value of its mean and its standard deviation . A few details of the normal curve merit special attention. The bell-shaped curve 1 is sym- metric about its mean , which locates the peak of the bell (see Figure 5). The interval run- ning one standard deviation in each direction from has a probability of .683, the interval from − 2 to + 2 has a probability of .954, and the interval from − 3 to + 3 has a probability of .997. It is these probabilities that give rise to the empirical rule stated in Chapter 2. The curve never reaches 0 for any value of x, but because the tail areas outside ( − 3, + 3 ) are very small, we usually terminate the graph at these points. A Normal Distribution has a bell-shaped density as shown in Figure 5. - William DeCoursey(Author)
- 2003(Publication Date)
- Newnes(Publisher)
157 CHAPTER 7 The Normal Distribution This chapter requires a good knowledge of the material covered in sections 2.1, 2.2, 3.1, 3.2, and 4.4. Chapter 6 is also helpful as background. The Normal Distribution is the most important of all probability distributions. It is applied directly to many practical problems, and several very useful distributions are based on it. We will encounter these other distributions later in this book. 7.1 Characteristics Many empirical frequency distributions have the following characteristics: 1. They are approximately symmetrical, and the mode is close to the centre of the distribution. 2. The mean, median, and mode are close together. 3. The shape of the distribution can be approximated by a bell: nearly flat on top, then decreasing more quickly, then decreasing more slowly toward the tails of the distribution. This implies that values close to the mean are relatively frequent, and values farther from the mean tend to occur less frequently. Remember that we are dealing with a random variable, so a frequency distribution will not fit this pattern exactly. There will be random variations from this general pattern. Remember also that many frequency distributions do not conform to this pattern. We have already seen a variety of frequency distributions in Chapter 4, and many other types of distribution occur in practice. Example 4.2 showed data on the thickness of a particular metal part of an optical instrument as items came off a production line. A histogram for 121 items is shown in Figure 4.4, reproduced here. Figure 4.4: Histogram of Thickness of Metal Part 0 10 20 30 40 50 Class Frequency per Class Width of 0.05 mm 3.220 3.270 3.320 3.370 3.420 3.470 3.520 3.570 Thickness, mm Thickness of Part Relative Class Frequency 0 0.083 0.165 0.248 0.331 0.413 Chapter 7 158 We can see that the characteristics stated above are present, at least approxi-mately, in Figure 4.4.- eBook - PDF
Comparative Analysis Of Nations
Quantitative Approaches
- Robert Perry(Author)
- 2019(Publication Date)
- Routledge(Publisher)
Figure 4. 3 maps out in detail the first three standard areas under a curve. This figure is virtually identical to Figure 3.2. However, Figure 4.3 partitions the curve into stan-dardized areas on either side of the mean. Each dotted line in Figure 4.3 demarcates the boundary between standard areas under the normal curve. In Figure 3.2, point cis equiv-alent to the -1 standard deviation threshold in Figure 4.3, while point din Figure 3.2 is equivalent to the+ 1 standard deviation threshold in Figure 4.3, and point x in Figure 3.2 represents the value 0 (the mean) in Figure 4.3. The middle solid line divides the distri-bution of values in half: To the right of this middle line all values in the sample are larger than the mean value, and to the left, all values are smaller than the mean of the sample. If a country had a value equal to the mean, that country's standard deviation would be zero (0), and it would be located squarely on the center line. Finally, the Normal Distribution -3 The Role if the Normal Distribution in Cross-National Research -2 -l I 0 68.26% 95.44% 99.72% +l Standard Deviation Ranges +2 +3 FIGURE 4.3 Standard Areas Under a Normal Curve Distribution and Respective Proportion of Scores Falling Within Specified Ranges 103 curve is, in theory, perfectly symmetrical. The standard areas to the left of the middle solid line are exactly equal to the shape (and size) of the standard areas to the right of the solid middle line. Recall, however, the Normal Distribution is an abstraction, per se, used as a reference point for interpretation and, ultimately, generalizations. It is important not to confuse the Normal Distribution with your sample distribution, which, as we have noted in Chapter 3, rarely conforms to the image of a perfect Normal Distribution. In-deed, a sample distribution assumes the properties of normality without having the per-fect symmetry representing a perfect Normal Distribution. - eBook - PDF
- Barbara Illowsky, Susan Dean(Authors)
- 2020(Publication Date)
- Openstax(Publisher)
The z-score allows us to compare data that are normally distributed but scaled differently. CHAPTER REVIEW 6.1 The Standard Normal Distribution A z-score is a standardized value. Its distribution is the standard normal, Z ~ N(0, 1). The mean of the z-scores is zero and the standard deviation is one. If z is the z-score for a value x from the Normal Distribution N(µ, σ), then z tells you how many standard deviations x is above—greater than—or below—less than—µ. 6.2 Using the Normal Distribution The Normal Distribution, which is continuous, is the most important of all the probability distributions. Its graph is bell- shaped. This bell-shaped curve is used in almost all disciplines. Since it is a continuous distribution, the total area under the curve is one. The parameters of the normal are the mean µ and the standard deviation σ. A special Normal Distribution, called the standard Normal Distribution, is the distribution of z-scores. Its mean is zero, and its standard deviation is one. FORMULA REVIEW 6.0 Introduction X ∼ N(μ, σ) μ = the mean, σ = the standard deviation 6.1 The Standard Normal Distribution Z ~ N(0, 1) z = a standardized value (z-score) mean = 0, standard deviation = 1 To find the k th percentile of X when the z-score is known, k = μ + (z)σ z-score: z = x – μ σ Z = the random variable for z-scores 6.2 Using the Normal Distribution Normal Distribution: X ~ N(µ, σ), where µ is the mean and σ is the standard deviation Standard Normal Distribution: Z ~ N(0, 1). Calculator function for probability: normalcdf (lower x value of the area, upper x value of the area, mean, standard deviation) Calculator function for the k th percentile: k = invNorm (area to the left of k, mean, standard deviation) PRACTICE 6.1 The Standard Normal Distribution 1. A bottle of water contains 12.05 fluid ounces with a standard deviation of 0.01 ounces. Define the random variable X in words. X = ____________. 2. A Normal Distribution has a mean of 61 and a standard deviation of 15. - Adam Prügel-Bennett(Author)
- 2020(Publication Date)
- Cambridge University Press(Publisher)
98 The Normal Distribution To check the normalisation of the Normal Distribution we change variables y = V ( x − μ), which gives ∞ −∞ N( x| μ, Σ) d x = 1 |2πΣ| ∞ −∞ e − y V T Σ −1 V y /2 J n i=1 dy i where J is the Jacobian defined by J = ∂x 1 ∂y 1 ∂x 1 ∂y 2 · · · ∂x 1 ∂yn ∂x 2 ∂y 1 ∂x 2 ∂y 2 · · · ∂x 2 ∂yn . . . . . . . . . . . . ∂xn ∂y 1 ∂xn ∂y 2 · · · ∂xn ∂yn . Since x = V T y + μ we find J = |V T |. The determinant of an orthogonal matrix is should be ±1. A matrix can be thought of as mapping points from one space to another space. If we map all points in some volume in the first space to the second space, then the ratio of volumes is given by the determinant (up to a sign describing whether that volume suffers a reflection or not). Because an orthogonal matrix just corresponds to a rotation and a possible reflection the determinant is ±1. Returning to the integral and using the diagonalisation formula we find ∞ −∞ N( x | μ, Σ) d x = 1 |2πΣ| ∞ −∞ e − y Λ −1 y /2 n i=1 dy i = 1 |2πΣ| n i=1 ∞ −∞ e −y 2 i /(2λ i ) dy i = 1 |2πΣ| n i=1 2 π λ i = (2 π) n/2 n i=1 λ i |2πΣ| . If M is an n × n matrix then |a M| = a n |M|. Thus the factors of 2 π cancel each other out. Using the property of the determinant |A B| = |A| × |B| (which immediately implies |A B C| = |A| × |B| × |C|), |Σ| = |VΛV T | = |V| × |Λ| × |V T | = |Λ|, since the determinants of the orthogonal matrix are equal to ±1. However, the determinant of a diagonal matrix is equal to the product of its diagonal elements so that |Λ| = n i=1 λ i , which completes our verification of the normalisation of the Normal Distribution. It follows from this derivation that if X ∼ N( μ, Σ) where Σ = VΛV T then Y = Λ −1/2 V( X − μ) will be distributed according to N(0, I). That is, the components of Y are independent normally distributed variables with zero mean and unit variance.
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.