Mathematics
Triangle Rules
The Triangle Rules in mathematics refer to the set of rules and properties that govern the relationships between the sides and angles of a triangle. These rules include the Pythagorean theorem, the laws of sines and cosines, and the properties of similar triangles. Understanding and applying these rules is essential for solving problems involving triangles in geometry and trigonometry.
Written by Perlego with AI-assistance
Related key terms
1 of 5
11 Key excerpts on "Triangle Rules"
- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Learning Press(Publisher)
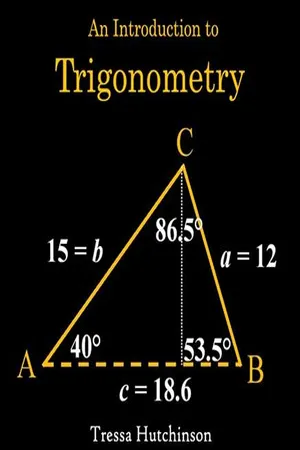
________________________ WORLD TECHNOLOGIES ________________________ Chapter 5 Common Laws & Formulas in Trigonometry 1. Law of sines A triangle In trigonometry, the law of sines (also known as the sine law , sine formula , or sine rule ) is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles. According to the law, where a , b , and c are the lengths of the sides of a triangle, and A , B , and C are the opposite angles (see the figure above). Sometimes the law is stated using the reciprocal of this equation: The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the formula gives two possible values for the enclosed angle, leading to an ambiguous case . ________________________ WORLD TECHNOLOGIES ________________________ The law of sines is one of two trigonometric equations commonly applied to find lengths and angles in a general triangle, the other being the law of cosines. Examples The following are examples of how to solve a problem using the law of sines: Given: side a = 20, side c = 24, and angle C = 40° Using the law of sines, we conclude that Or another example of how to solve a problem using the law of sines: If two sides of the triangle are equal to R and the length of the third side, the chord, is given as 100 feet and the angle C opposite the chord is given in degrees, then and Numeric problems Like the law of cosines, although the law of sines is mathematically true, it has problems for numeric use. Much precision may be lost if an arcsine is computed when the sine of an angle is close to one. ________________________ WORLD TECHNOLOGIES ________________________ Some applications • The sine law can be used to prove the angle sum identity for sine when α and β are each between 0 and 90 degrees. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 12 Common Laws & Formulas in Trigonometry 1. Law of sines A triangle In trigonometry, the law of sines (also known as the sine law , sine formula , or sine rule ) is an equation relating the lengths of the sides of an arbitrary triangle to the sines of its angles. According to the law, where a , b , and c are the lengths of the sides of a triangle, and A , B , and C are the opposite angles (see the figure above). Sometimes the law is stated using the reciprocal of this equation: The law of sines can be used to compute the remaining sides of a triangle when two angles and a side are known—a technique known as triangulation. It can also be used when two sides and one of the non-enclosed angles are known. In some such cases, the formula gives two possible values for the enclosed angle, leading to an ambiguous case . ________________________ WORLD TECHNOLOGIES ________________________ The law of sines is one of two trigonometric equations commonly applied to find lengths and angles in a general triangle, the other being the law of cosines. Examples The following are examples of how to solve a problem using the law of sines: Given: side a = 20, side c = 24, and angle C = 40° Using the law of sines, we conclude that Or another example of how to solve a problem using the law of sines: If two sides of the triangle are equal to R and the length of the third side, the chord, is given as 100 feet and the angle C opposite the chord is given in degrees, then and Numeric problems Like the law of cosines, although the law of sines is mathematically true, it has problems for numeric use. Much precision may be lost if an arcsine is computed when the sine of an angle is close to one. ________________________ WORLD TECHNOLOGIES ________________________ Some applications • The sine law can be used to prove the angle sum identity for sine when α and β are each between 0 and 90 degrees. - Alan Sultan, Alice F. Artzt(Authors)
- 2017(Publication Date)
- Routledge(Publisher)
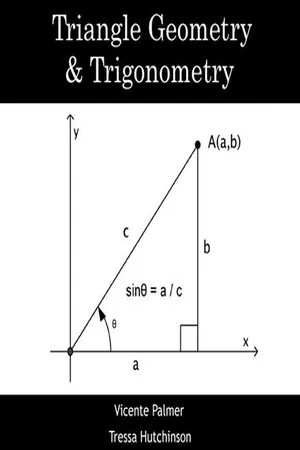
Chapter 5The Triangle: Its Study and Consequences5.1 IntroductionIf you ask adults what theorem they remember from their study of mathematics, they will most probably say, the Pythagorean Theorem. Why should this theorem, usually studied in secondary school, make such a lasting impression? As will be demonstrated in this chapter, this one theorem concerning the relationship of the sides of a right triangle can be extended to the study of (a) all types of triangles, (b) relationships concerning circles, (c) key trigonometric relationships, and (d) concepts of area. It is really quite amazing!To begin, we need only remember a few basic definitions: In a right triangle with acute angle, A ,
Also, we easily see thatsin A =,length of side opposite Alength of hypotenusecos A =,length of side adjacent to Alength of hypotenusetan A =.length of side opposite to Alength of side adjacent to Atan A =.sin Acos AWe begin by discussing how the Pythagorean Theorem can be extended to generate the Law of Cosines and then follow it with the study of the Law of Sines. What is different about this chapter is that these will then be used to prove all the congruence laws, all the main similarity laws, facts about circles, and a host of other relationships in triangles. While people normally think that trigonometry follows geometry, we have demonstrated that we can do things in reverse by showing how the theorems of geometry can be derived from theorems in trigonometry.We will use the following notational conventions throughout: When we say that ∡A = ∡B , we mean that the measures of the two angles are equal. An alternate way of saying this is that ∡A is congruent to ∡B. AB will represent the length ofWhen we say that AB = CD we are saying that the measures ofA B¯andA B¯are equal, or equivalently, that AB is congruent to CD .C D¯5.2 The Law of Cosines and Surprising ConsequencesLaunchDraw a large triangle on a clean sheet of paper. Then measure the length of each of the sides of the triangle you have drawn. Using these same three lengths, try to draw another triangle that is NOT congruent to the first one you drew. Could you do it? Why or why not?- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Orange Apple(Publisher)
This triangle can be constructed by first constructing a circle of diameter 1, and inscribing in it two of the angles of the triangle. The length of the sides of that triangle will be sinα , sinβ and sinγ . The side whose length is sinα is opposite to the angle whose measure is α , etc. The law of cosines, or cosine rule, connects the length of an unknown side of a triangle to the length of the other sides and the angle opposite to the unknown side. As per the law: For a triangle with length of sides a , b , c and angles of α , β , γ respectively, given two known lengths of a triangle a and b , and the angle between the two known sides γ (or the angle opposite to the unknown side c ), to calculate the third side c , the following formula can be used: If the lengths of all three sides of any triangle are known the three angles can be calculated: ________________________ WORLD TECHNOLOGIES ________________________ The law of tangents or tangent rule, is less known than the other two. It states that: It is not used very often, but can be used to find a side or an angle when you know two sides and an angle or two angles and a side. Further formulas for general Euclidean triangles The following formulas are also true for all Euclidean triangles: and , and equivalently for m b and m c , relating the medians and the sides; for semiperimeter s , where the bisector length is measured from the vertex to where it meets the opposite side; and the following formulas involving the circumradius R and the inradius r : in terms of the altitudes, , and ________________________ WORLD TECHNOLOGIES ________________________ . Suppose two adjacent but non-overlapping triangles share the same side of length f and share the same circumcircle, so that the side of length f is a chord of the circumcircle and the triangles have side lengths ( a , b , f ) and ( c , d , f ), with the two triangles together forming a cyclic quadrilateral with side lengths in sequence ( a , b , c , d ). - eBook - PDF
- Cynthia Y. Young(Author)
- 2021(Publication Date)
- Wiley(Publisher)
1 *Section 1.5, Example 7 and Exercises 72–74 and 79–80. Thousands of years later, we still find applications of right triangle trigonometry today in sports, surveying, navigation,* and engineering. CHAPTER 1 Right Triangle Trigonometry To the ancient Greeks, trigonometry was the study of right triangles. Trigonometric functions (sine, cosine, tangent, cotangent, secant, and cosecant) can be defined as right triangle ratios (ratios of the lengths of sides of a right triangle). 1.1 Angles, Degrees, and Triangles • Angles and Degree Measure • Triangles • Special Right Triangles 1.2 Similar Triangles • Finding Angle Measures Using Geometry • Classification of Triangles 1.3 Definition 1 of Trigonometric Functions: Right Triangle Ratios • Trigonometric Functions: Right Triangle Ratios • Cofunctions RIGHT TRIANGLE TRIGONOMETRY 1.4 Evaluating Trigonometric Functions: Exactly and with Calculators • Evaluating Trigonometric Functions Exactly for Special Angle Measures: 30°, 45°, and 60° • Using Calculators to Evaluate (Approximate) Trigonometric Function Values • Representing Partial Degrees: DD or DMS 1.5 Solving Right Triangles • Accuracy and Significant Digits • Solving a Right Triangle Given an Acute Angle Measure and a Side Length • Solving a Right Triangle Given the Lengths of Two Sides VitalyEdush/Getty Images, Inc. LEARNING OBJECTIVES • Understand degree measure. • Learn the conditions that make two triangles similar. • Define the six trigonometric functions as ratios of lengths of the sides of right triangles. • Evaluate trigonometric functions exactly and with calculators. • Solve right triangles. 2 CHAPTER 1 Right Triangle Trigonometry In This Chapter We will review angles, degree measure, and special right triangles. We will discuss the properties of similar triangles. We will use the concept of similar right triangles to define the six trigonometric functions as ratios of the lengths of the sides of right triangles (right triangle trigonometry). - eBook - PDF
Maths: A Student's Survival Guide
A Self-Help Workbook for Science and Engineering Students
- Jenny Olive(Author)
- 2003(Publication Date)
- Cambridge University Press(Publisher)
4 Some trigonometry and geometry of triangles and circles This chapter reminds you of what trig is for, and how it works in triangles. It also explains some of the special geometrical properties of triangles and circles, because they may be very useful to you in applications of maths to your own special subject area. The chapter is divided into the following sections. 4.A Trigonometry in right-angled triangles (a) Why use trig ratios? (b) Pythagoras’ Theorem, (c) General properties of triangles, (d) Triangles with particular shapes, (e) Congruent triangles – what are they, and when? (f) Matching ratios given by parallel lines, (g) Special cases – the sin, cos and tan of 30°, 45° and 60°, (h) Special relations of sin, cos and tan 4.B Widening the field in trigonometry (a) The Sine Rule for any triangle, (b) Another area formula for triangles, (c) The Cosine Rule for any triangle 4.C Circles (a) The parts of a circle, (b) Special properties of chords and tangents of circles, (c) Special properties of angles in circles, (d) Finding and working with the equations which give circles, (e) Circles and straight lines – the different possibilities, (f) Finding the equations of tangents to circles 4.D Using radians (a) Measuring angles in radians, (b) Finding the perimeter and area of a sector of a circle, (c) Finding the area of a segment of a circle, (d) What do we do if the angle is given in degrees? (e) Very small angles in radians – why we like them 4.E Tidying up – some thinking points returned to (a) The sum of interior and exterior angles of polygons, (b) Can we draw circles round all triangles and quadrilaterals? 4.A Trigonometry in right-angled triangles 4.A. (a) Why use trig ratios? When you began learning trigonometry (often referred to as ‘trig’), you will have started by working with right-angled triangles. Since my policy is to make sure of the groundwork for each topic before going further, I will start from here, too. - eBook - PDF
- H. S. M. Coxeter, S. L. Greitzer(Authors)
- 1967(Publication Date)
- American Mathematical Society(Publisher)
C H A P T E R 1 Points and Lines Connected with a Triangle With a literature much vaster than those of algebra and arithmetic combined, and at least as extensive as that of analysis, geometry is a richer treasure house of more inter- esting and half-forgotten things, which a hurried generation has no leisure to enjoy, than any other division of mathe- matics. E. T. BdL The purpose of this chapter is to recall some of these half-forgotten things to which Dr. Bell referred, to derive some new theorems, developed since Euclid, and to apply our findings to interesting situations. We consider an arbitrary triangle and its most famous associated points and lines: the circumcenter, medians, centroid, angle-bisectors, incenter, excenters, altitudes, orthocenter, Euler line, and nine-point center. The angle-bisectors lead naturally to a digression on the Steiner- Lehmus theorem, which was believed for a hundred years to be difficult to prove, though we see now that it is really quite easy. Finally, from a triangle and a point P of general position, we derive a new triangle whose vertices are the feet of the perpendiculars from P to the sides of the given triangle. This idea leads to some amusing developments, some of which are postponed till the next chapter. 1.1 The extended Law of Sines The Law of Sines is one trigonometric theorem that will be used fre- quently. Unfortunately, it usually appears in texts in a truncated form that is not so useful as an extended theorem could be. We take the liberty, therefore, of proving the Law of Sines in the form that we desire. 1 2 POINTS, LINES CONNECTED WITH A TRIANGLE Figure 1.1A We start with AABC (labeled in the customary manner) and circum- scribe about it a circle with center at 0 and with radius equal to R units, as shown in Figures 1.1A and 1.1B. We draw the diameter CJ, and the chord B J.t In both of the situations shown, L CB J is a right angle, since it is inscribed in a semicircle. - eBook - ePub
- (Author)
- 2008(Publication Date)
- Trade Paper Press(Publisher)
Trigonometry solves problems relating to plane and spherical triangles. Its principles are based on the fixed proportions of sides for a particular angle in a right-angled triangle, the simplest of which are known as the sine, cosine, and tangent (so-called trigonometrical ratios). Trigonometry is of practical importance in navigation, surveying, and simple harmonic motion in physics.trigonometry At its simplest level, trigonometry deals with the relationships between the sides and angles of triangles. Unknown angles or lengths are calculated by using trigonometrical ratios such as sine, cosine, and tangent.Using trigonometry, it is possible to calculate the lengths of the sides and the sizes of the angles of a right-angled triangle as long as one angle and the length of one side are known, or the lengths of two sides. The longest side, which is always opposite to the right angle, is called the hypotenuse . The other sides are named depending on their position relating to the angle that is to be found or used: the side opposite this angle is always termed opposite and that adjacent is the adjacent . So the following trigonometrical ratios are used:sine
The sine is the function of an angle in a right-angled triangle which is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse (the longest side). It is usually shortened to sin .sine The sine is a function of an angle in a right-angled triangle found by dividing the length of the side opposite the angle by the length of the hypotenuse (the longest side). Sine (usually abbreviated sin) is one of the fundamental trigonometric ratios.Various properties in physics vary sinusoidally; that is, they can be represented diagrammatically by a sine wave (a graph obtained by plotting values of angles against the values of their sines). Examples include simple harmonic motion, such as the way alternating current (AC) electricity varies with time.sine (left) The sine of an angle; (right) constructing a sine wave. The sine of an angle is a function used in the mathematical study of the triangle. If the sine of angle β is known, then the hypotenuse can be found given the length of the opposite side, or the opposite side can be found from the hypotenuse. Within a circle of unit radius (left), the height P1 ,A1 equals the sine of angle P1 0A1 - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
Another interpretation of this theorem is that every triangle with angles α , β and γ is similar to a triangle with side lengths equal to sinα , sinβ and sinγ . This triangle can be constructed by first constructing a circle of diameter 1, and inscribing in it two of the angles of the triangle. The length of the sides of that triangle will be sinα , sinβ and sinγ . The side whose length is sinα is opposite to the angle whose measure is α , etc. The law of cosines, or cosine rule, connects the length of an unknown side of a triangle to the length of the other sides and the angle opposite to the unknown side. As per the law: For a triangle with length of sides a , b , c and angles of α , β , γ respectively, given two known lengths of a triangle a and b , and the angle between the two known sides γ (or the angle opposite to the unknown side c ), to calculate the third side c , the following formula can be used: If the lengths of all three sides of any triangle are known the three angles can be calculated: ________________________ WORLD TECHNOLOGIES ________________________ The law of tangents or tangent rule, is less known than the other two. It states that: It is not used very often, but can be used to find a side or an angle when you know two sides and an angle or two angles and a side. Further formulas for general Euclidean triangles The following formulas are also true for all Euclidean triangles: and , and equivalently for m b and m c , relating the medians and the sides; for semiperimeter s , where the bisector length is measured from the vertex to where it meets the opposite side; and the following formulas involving the circumradius R and the inradius r : in terms of the altitudes, , and ________________________ WORLD TECHNOLOGIES ________________________ . - eBook - PDF
How to Think Like a Mathematician
A Companion to Undergraduate Mathematics
- Kevin Houston(Author)
- 2009(Publication Date)
- Cambridge University Press(Publisher)
Indeed there is one. Exercise 19.3 Find a theorem that relates angles and lengths in a triangle. Observe the detail There are not many details to observe in Pythagoras’ Theorem as it is rather simple. The detail to remember perhaps is that the triangle is right-angled – not, for example, isosceles. (See the exercises at the end of the chapter for some infamous examples of mistakes with the statement.) Classify what the theorem does and how it can be used We have already discussed above what the theorem does: it allows us to calculate the length of a side of a triangle given the lengths of the other two. Draw a picture Since this is a geometric theorem – it is about triangles – then we have good reason to draw a picture. In this case draw lots of triangles and measure the lengths. Do the lengths satisfy the equation? They should do but remember we can only measure lengths approximately. The classic picture is the (3, 4, 5)-triangle given in Figure 19.2. This is often mistakenly given as a proof of the theorem. However, it is only a single example, not a proof. 4 3 5 Figure 19.2 The classic (3, 4, 5)-triangle Study of the theorem 129 Apply the theorem to simple examples In drawing the pictures we have already applied the theorem to simple examples such as the (3, 4, 5)-triangle. Apply the theorem to trivial and extreme examples The assumptions concern right-angled triangles. What are trivial and extreme examples of such objects? I would say that the trivial examples are when a = 1 and b = 1 so c = √ 2. This is a triangle with two sides of rational lengths and one side of irrational length. One could view this as a counterexample to the statement ‘If two sides of a triangle are rational, then so is the third.’ Another useful example is a = 1, b = 2, and so c = √ 5. This just shows us what happens when one side is twice the length of the other. Another interesting example is a = 1, b = √ 2, and so c = √ 3. I like this, it involves the first three numbers 1, 2 and 3. - eBook - PDF
- Dale Ewen(Author)
- 2018(Publication Date)
- Cengage Learning EMEA(Publisher)
OBJECTIVES ◆ Write the trigonometric ratios for the sine, cosine, and tangent of an angle using the basic terms of a right triangle. ◆ Find the value of a trigonometric ratio using a scientific calculator. ◆ Use a trigonometric ratio to find angles. ◆ Use a trigonometric ratio to find sides. ◆ Solve a right triangle. ◆ Solve application problems involving trigonometric ratios and right triangles. Computer Support Specialist Computer technician reparing a computer CHAPTER 13 Right Triangle Trigonometry CandyBox Images/Shutterstock.com 424 CHAPTER 13 ◆ Right Triangle Trigonometry Trigonometric Ratios 13.1 Many applications in science and technology require the use of triangles and trigonometry. Early applications of trigonometry, beginning in the second century b.c., were in astronomy, surveying, and navigation. Applications that you may study include electronics, the motion of projectiles, light refraction in optics, and sound. In this chapter, we consider only right triangles. A right triangle has one right angle, two acute angles, a hypotenuse, and two legs. The right angle, as shown in Figure 13.1, is usually labeled with the capital letter C . The vertices of the two acute angles are usually la- beled with the capital letters A and B . The hypotenuse is the side opposite the right angle, the longest side of a right triangle, and is usually labeled with the lowercase letter c . The legs are the sides opposite the acute angles. The leg (side) opposite angle A is labeled a , and the leg opposite angle B is labeled b . Note that each side of the triangle is labeled with the lowercase of the letter of the angle opposite that side. The two legs are also named as the side opposite angle A and the side adjacent to (or next to) angle A or as the side opposite angle B and the side adjacent to angle B .
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.