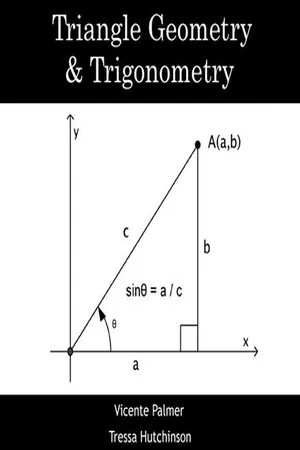
Mathematics
Types of Triangles
Triangles can be classified into different types based on their side lengths and angles. The three main types are equilateral triangles (all sides and angles are equal), isosceles triangles (two sides and two angles are equal), and scalene triangles (all sides and angles are different). These classifications help in understanding and solving geometric problems involving triangles.
Written by Perlego with AI-assistance
Related key terms
1 of 5
10 Key excerpts on "Types of Triangles"
- eBook - ePub
- Mark Ryan(Author)
- 2016(Publication Date)
- For Dummies(Publisher)
Part 3Triangles: Polygons of the Three-Sided Variety
IN THIS PART … Get familiar with triangle basics. Have fun with right triangles. Work on congruent triangle proofs.Passage contains an image Chapter 7
Grasping Triangle Fundamentals
IN THIS CHAPTER Looking at a triangle’s sides: Equal or unequal Uncovering the triangle inequality principle Classifying triangles by their angles Calculating the area of a triangle Finding the four “centers” of a triangleConsidering that it’s the runt of the polygon family, the triangle sure does play a big role in geometry. Triangles are one of the most important components of geometry proofs (you see triangle proofs in Chapter 9 ). They also have a great number of interesting properties that you might not expect from the simplest possible polygon. Maybe Leonardo da Vinci (1452–1519) was on to something when he said, “Simplicity is the ultimate sophistication.”In this chapter, I take you through the triangle basics — their names, sides, angles, and area. I also show you how to find the four “centers” of a triangle.Taking In a Triangle’s Sides
Triangles are classified according to the length of their sides or the measure of their angles. These classifications come in threes, just like the sides and angles themselves. That is, a triangle has three sides, and three terms describe triangles based on their sides; a triangle also has three angles, and three classifications of triangles are based on their angles. I talk about classifications based on angles in the upcoming section “Getting to Know Triangles by Their Angles .”The following are triangle classifications based on sides:- Scalene triangle: A scalene triangle is a triangle with no congruent sides
- Isosceles triangle: An isosceles triangle is a triangle with at least two congruent sides
- Equilateral triangle: A equilateral triangle is a triangle with three congruent sides
Because an equilateral triangle is also isosceles, all triangles are either scalene or isosceles. But when people call a triangle isosceles, they’re usually referring to a triangle with only two equal sides, because if the triangle had three equal sides, they’d call it equilateral. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 1 Introduction to Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} (for equilateral) Area various methods; see below Internal angle (degrees) 60° (for equilateral) A triangle is one of the basic shapes of geometry: a polygon with three corners or ver-tices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of Triangles Euler diagram of Types of Triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. equilateral triangles are isosceles. By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all equilateral triangles isosceles triangles. The 45-45-90 Right Triangle, which appears in the Tetrakis square tiling, is isosceles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Learning Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter- 1 Introduction to Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} (for equilateral) Area various methods; see below Internal angle (degrees) 60° (for equilateral) A triangle is one of the basic shapes of geometry: a polygon with three corners or ver-tices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of Triangles Euler diagram of Types of Triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. equilateral triangles are isosceles. By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all equilateral triangles isosceles triangles. The 45-45-90 Right Triangle, which appears in the Tetrakis square tiling, is isosceles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 1 Introduction to Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} (for equilateral) Area various methods; see below Internal angle (degrees) 60° (for equilateral) A triangle is one of the basic shapes of geometry: a polygon with three corners or verti-ces and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of Triangles Euler diagram of Types of Triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. equilateral triangles are isosceles. By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all equilateral triangles isosceles triangles. The 45-45-90 Right Triangle, which appears in the Tetrakis square tiling, is isosceles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 4 Triangle and Congruence Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of Triangles By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all equilateral triangles isosceles triangles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. . Equilateral Isosceles Scalene By internal angles Triangles can also be classified according to their internal angles, measured here in degrees. • A right triangle (or right-angled triangle , formerly called a rectangled triangle ) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side of the right triangle. The other two sides are called the legs or catheti (singular: cathetus ) of the triangle. - No longer available |Learn more
College Geometry
A Unified Approach
- (Author)
- 2014(Publication Date)
- Orange Apple(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter- 4 Triangle and Congruence Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of Triangles By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all equilateral triangles isosceles triangles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. . Equilateral Isosceles Scalene By internal angles Triangles can also be classified according to their internal angles, measured here in degrees. • A right triangle (or right-angled triangle , formerly called a rectangled triangle ) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side of the right triangle. The other two sides are called the legs or catheti (singular: cathetus ) of the triangle. - Available until 8 Feb |Learn more
- J Daniels, M Kropman, J Daniels, M Kropman(Authors)
- 2014(Publication Date)
- Future Managers(Publisher)
6 MODULE Triangles 6.1 Properties of triangles On completion of this section, you should be able to: 6.1.1 Calculate an unknown interior angle of a triangle when two interior angles are given (the sum of the interior angles of a triangle is equal to 180°), as well as name and apply the properties of an isosceles triangle 6.1.2 Write down the relation between an exterior angle and the opposite interior angles of a triangle 6.1.3 Name the conditions for two triangles to be congruent 6.1.4 Draw similar triangles, write down corresponding angles and calculate the ratio of the corresponding sides. 6.2 Pythagoras’ theorem On completion of this section, you should be able to: 6.2.1 Calculate the unknown side of a right-angled triangle by applying Pythagoras’ theorem 6.2.2 Construct a right-angled triangle with the 3-4-5 method. 188 Module 6 • Triangles 6.1 Properties of triangles Geometry is the study of the properties and relationships of points, lines and surfaces in space. Geometry is used in engineering (electricity and electronics), art, architecture (planning shapes of buildings, roads and bridges), robotics, land surveys, machines, cars, navigators (guidance of boats, planes and space ships), and much more. In ancient Greek, geo means earth and metron means measurement. A polygon is a flat shape that is completely enclosed by 3 or more straight lines, such as a triangle (3 sides), a quadrilateral (4 sides) and a hexagon (6 sides). A triangle is a polygon with three edges. Basic triangles and their properties will be covered in this section. Pre-knowledge • Lines and angles Description Example Explanation Adjacent angles on a straight line add up to 180°. x y A B or C x + y = 180° These angles are called supplementary angles AB ˆ C = 180° or ∠ ABC = 180° Revolution A Â = 360° (revolution) 90° 270° 180° 0° 360° - Allen Ma, Amber Kuang(Authors)
- 2022(Publication Date)
- For Dummies(Publisher)
165. 14 An isosceles triangle is a triangle that has two congruent sides. In this isosceles triangle, because E is the vertex, DF FE . Set the two sides equal to each other to determine the value of x: 2 10 3 4 10 4 14 x x x x 166. 46 An equilateral triangle is a triangle that has all three sides congruent. Set any two sides of the triangle equal to each other to determine the value of x: 2 5 14 22 1 5 14 22 1 5 36 24 . . . x x x x x To find the length of LI , plug 24 in for x in either of the expressions: LN 24 22 46 167. 9 Using the given relationships, let HP x PY x HY x 3 2 3 A right triangle is a triangle whose sides satisfy the Pythagorean theorem. Set up the Pythagorean theorem and solve for x: a b c x x x x x x x x x x 2 2 2 2 2 2 2 2 2 2 3 2 3 6 9 4 1 2 9 6 9 2 12 + = + + = -+ + + = -+ + = -( ) ( ) ( ) x x x x x x x x x x + = -= -= -= = 9 6 2 12 0 2 18 0 2 9 0 9 2 2 ( ) or Therefore, HP x 9 . 188 PART 2 The Answers ANSWERS 101–200 168. 4 An isosceles triangle is a triangle that has two congruent sides. In this isosceles triangle, because H is the vertex, SH HE . Set the two sides equal to each other to determine the value of x: x x x x x x x x 2 2 12 12 0 3 4 0 3 4 ( )( ) or 169. 4 An equilateral triangle is a triangle that has all three sides congruent. Set any two sides of the triangle equal to each other to determine the value of x: x x x 3 3 3 3 64 64 4 170. Right The sum of the three angles in a triangle is 180°: 4 0 50 180 90 180 90 x x x Because the largest angle in the triangle is 90°, the triangle is a right triangle. 171. Equiangular The sum of the three angles in a triangle is 180°: 6 0 60 180 120 180 60 x x x Because all three angles are equal, the triangle is equiangular. 172. Acute The sum of the three angles in a triangle is 180°: 50 70 180 120 180 60 x x x Because the largest angle in the triangle is 90 and no angles are equal, the triangle is acute.- Available until 8 Feb |Learn more
- J Daniels, N Solomon, J Daniels, N Solomon(Authors)
- 2014(Publication Date)
- Future Managers(Publisher)
X U T R S O 25° a c b Determine the numerical values of a , b and c , with reasons. 206 Mathematics: Hands-On Training Geometry of triangles A triangle is defined as a polygon with three angles and therefore three sides or edges, which are line segments. c b a B C A Triangles are classified according to their sides or interior angles. Type of triangle Description Sketch Scalene triangle Sides are all different lengths and all three angles different Isosceles triangle Two equal sides and the angles opposite the sides are also equal x x Equilateral triangle All three sides are equal and each angle measures 60° 60° 60° 60° Acute-angled triangle All interior angles are less than 90° x z y Obtuse-angled triangle One interior angle is more than 90° x Right-angled triangle One interior angle is a right angle, that is, 90° Two main properties of the interior angles of a triangle Description Sketch The sum of the interior angles of a triangle is equal to 180° x y z ˆ ˆ ˆ x y z + + = ° 180 The exterior angle of a triangle is equal to the sum of the two opposite interior angles x y z ˆ ˆ ˆ z x y = + Note Isosceles is a Greek word, meaning “equal legs”. 207 Chapter 3 Space, shape and measurement Additional to the main properties of the interior angles of a triangle, the Theorem of Pythagoras states that in a right-angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides. c b a a 2 + b 2 = c 2 Example 5 3 BCD is an isosceles triangle with BC = BD. A B C D 110° z y x Compute the numerical values x , y and z , with reasons. Solution If 3 BCD is an isosceles triangle with BC = BD, BC ˆ D = BDC ˆ , therefore ˆ x = ˆ z . BC ˆ D + BDC ˆ = ABD ˆ • Exterior angle of a triangle is equal to the sum of the two opposite interior angles. ˆ x + ˆ z = 110° • Substitute ˆ z = ˆ x , as 3 BCD is an isosceles triangle. ˆ x + ˆ x = 110° 2 ˆ x = 110° ˆ x = 55° CBD ˆ + ABD ˆ = 180° • Straight angle, ABC ˆ = 180°. - eBook - PDF
Dr. Math Introduces Geometry
Learning Geometry is Easy! Just ask Dr. Math!
- (Author)
- 2004(Publication Date)
- Jossey-Bass(Publisher)
4. Let ABC be a triangle, and consider the following figure: Note that the three angles marked with ✽ add up to one com- plete turn—that is, 360 degrees. Note also that each of the angles marked with ✽ makes a straight angle when added to one of the angles of ABC. So the three angles marked with ✽ added to the angles of ABC add up to 3 ⋅ 180° = 540°. That leaves 540° – 360° = 180° for the angles of ABC. —Dr. Math, The Math Forum Introduction to Two-Dimensional (2-D) Geometric Figures 41 42 Dr. Math Introduces Geometry 4 4 Quadrilaterals A polygon (any figure made up of connected straight line segments) that has four sides is called a quadrilateral—remember “lateral” means “side,” as in “equilateral,” and “quad” means “four.” But just knowing something’s a quadrilateral doesn’t tell you much about its angles or sides except that there are four of them. In this section, we’ll discuss the various types of quadrilaterals. Dear Dr. Math, I really need to know the seven types of quadrilaterals. Please give me a hand! Yours truly, Lorraine The Seven Quadrilat- erals Introduction to Two-Dimensional (2-D) Geometric Figures 43 Dear Lorraine, I think you’re talking about these: Here are the things you ought to know: 1. A rhombus is an equilateral quadrilateral (all sides have the same length). 2. A rectangle is an equiangular quadrilateral (all angles have the same measure). 3. A square is an equilateral, equiangular quadrilateral, or 44 Dr. Math Introduces Geometry simply a regular quadrilateral. Every square is also a rhombus (because it’s equilateral) and a rectangle (because it’s equiangular). 4. A parallelogram is a quadrilateral with exactly two pairs of parallel sides. Every rhombus is a parallelogram and so is every rectangle. And if every rectangle is a parallelogram, then so is every square. 5. There are two definitions commonly used for trapezoid. The traditional American definition is a quadrilateral with exactly one pair of parallel sides.
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.