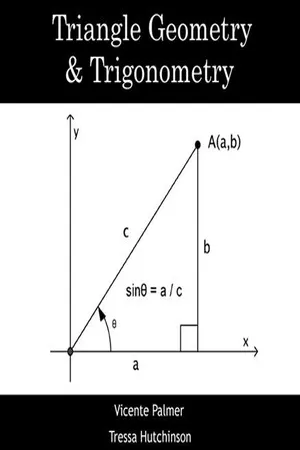
Mathematics
Equilateral Triangles
Equilateral triangles are a type of triangle where all three sides are of equal length. Additionally, all three angles in an equilateral triangle are also equal, each measuring 60 degrees. This makes equilateral triangles a special case of both equiangular and equilateral polygons.
Written by Perlego with AI-assistance
Related key terms
1 of 5
11 Key excerpts on "Equilateral Triangles"
- No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 1 Introduction to Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} (for equilateral) Area various methods; see below Internal angle (degrees) 60° (for equilateral) A triangle is one of the basic shapes of geometry: a polygon with three corners or ver-tices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of triangles Euler diagram of types of triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. Equilateral Triangles are isosceles. By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all Equilateral Triangles isosceles triangles. The 45-45-90 Right Triangle, which appears in the Tetrakis square tiling, is isosceles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Learning Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter- 1 Introduction to Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} (for equilateral) Area various methods; see below Internal angle (degrees) 60° (for equilateral) A triangle is one of the basic shapes of geometry: a polygon with three corners or ver-tices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of triangles Euler diagram of types of triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. Equilateral Triangles are isosceles. By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all Equilateral Triangles isosceles triangles. The 45-45-90 Right Triangle, which appears in the Tetrakis square tiling, is isosceles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 1 Introduction to Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} (for equilateral) Area various methods; see below Internal angle (degrees) 60° (for equilateral) A triangle is one of the basic shapes of geometry: a polygon with three corners or verti-ces and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of triangles Euler diagram of types of triangles, using the definition that isosceles triangles have at least 2 equal sides, i.e. Equilateral Triangles are isosceles. By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all Equilateral Triangles isosceles triangles. The 45-45-90 Right Triangle, which appears in the Tetrakis square tiling, is isosceles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. - eBook - PDF
Maths: A Student's Survival Guide
A Self-Help Workbook for Science and Engineering Students
- Jenny Olive(Author)
- 2003(Publication Date)
- Cambridge University Press(Publisher)
We also see from this same diagram that, if we have a triangle with one side extended, then the exterior angle e is equal to a + b , the sum of the two interior opposite angles. This is shown drawn in on Figure 4.A.13 . 4.A. (d) Triangles with particular shapes Triangles can come in an infinite variety of shapes, but there are two particular types which have specific names. If a triangle has two sides equal then it is called isosceles (originally by the Greeks who were very keen on geometry – ‘iso’ means ‘equal’ and ‘sceles’ means ‘sides’. ‘Trigonometry’ also comes from the Greeks – ‘trigono’ is the Greek word for triangle.) 4.A Trigonometry in right-angled triangles 139 Figure 4.A.12 Figure 4.A.13 The two equal sides give these triangles a line of symmetry, so that one half folds exactly on to the other half, and the pair of angles opposite the equal sides are also equal. The line of symmetry divides the triangle into two equal right-angled triangles. (See Figure 4.A.14(a) .) The little dashes are there to mark the two equal sides. If a triangle has all three sides equal then it is called equilateral . Such a triangle is pictured in Figure 4.A.14(b) . It will have three lines of symmetry as shown, and will fit exactly onto itself three times in a complete turn. Therefore all its angles are equal, and so must be 60° each. All Equilateral Triangles can nest into each other, in any chosen corner. Some are shown here in Figure 4.A.15 . They are all similar to each other. (‘Similar’ in maths doesn’t just mean ‘more or less the same as’ but ‘an exact scale model of’ so that all the angles remain the same, and the pairs of sides are all in the same proportion.) 4.A. (e) Congruent triangles – what are they, and when? If two triangles are exactly the same size and shape so that they can be fitted onto each other exactly, they are called congruent . In this case, they will obviously have three equal pairs of angles and three equal pairs of sides. - eBook - ePub
- Mark Ryan(Author)
- 2016(Publication Date)
- For Dummies(Publisher)
Part 3Triangles: Polygons of the Three-Sided Variety
IN THIS PART … Get familiar with triangle basics. Have fun with right triangles. Work on congruent triangle proofs.Passage contains an image Chapter 7
Grasping Triangle Fundamentals
IN THIS CHAPTER Looking at a triangle’s sides: Equal or unequal Uncovering the triangle inequality principle Classifying triangles by their angles Calculating the area of a triangle Finding the four “centers” of a triangleConsidering that it’s the runt of the polygon family, the triangle sure does play a big role in geometry. Triangles are one of the most important components of geometry proofs (you see triangle proofs in Chapter 9 ). They also have a great number of interesting properties that you might not expect from the simplest possible polygon. Maybe Leonardo da Vinci (1452–1519) was on to something when he said, “Simplicity is the ultimate sophistication.”In this chapter, I take you through the triangle basics — their names, sides, angles, and area. I also show you how to find the four “centers” of a triangle.Taking In a Triangle’s Sides
Triangles are classified according to the length of their sides or the measure of their angles. These classifications come in threes, just like the sides and angles themselves. That is, a triangle has three sides, and three terms describe triangles based on their sides; a triangle also has three angles, and three classifications of triangles are based on their angles. I talk about classifications based on angles in the upcoming section “Getting to Know Triangles by Their Angles .”The following are triangle classifications based on sides:- Scalene triangle: A scalene triangle is a triangle with no congruent sides
- Isosceles triangle: An isosceles triangle is a triangle with at least two congruent sides
- Equilateral triangle: A equilateral triangle is a triangle with three congruent sides
Because an equilateral triangle is also isosceles, all triangles are either scalene or isosceles. But when people call a triangle isosceles, they’re usually referring to a triangle with only two equal sides, because if the triangle had three equal sides, they’d call it equilateral. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 8 Triangle and Circle Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . ________________________ WORLD TECHNOLOGIES ________________________ In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). Types of triangles By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all Equilateral Triangles isosceles triangles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. Equilateral Isosceles Scalene By internal angles Triangles can also be classified according to their internal angles, measured here in degrees. • A right triangle (or right-angled triangle , formerly called a rectangled triangle ) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side of the right triangle. The other two sides are called the legs or catheti (singular: cathetus ) of the triangle. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Library Press(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter 4 Triangle and Congruence Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of triangles By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all Equilateral Triangles isosceles triangles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. . Equilateral Isosceles Scalene By internal angles Triangles can also be classified according to their internal angles, measured here in degrees. • A right triangle (or right-angled triangle , formerly called a rectangled triangle ) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side of the right triangle. The other two sides are called the legs or catheti (singular: cathetus ) of the triangle. - No longer available |Learn more
College Geometry
A Unified Approach
- (Author)
- 2014(Publication Date)
- Orange Apple(Publisher)
________________________ WORLD TECHNOLOGIES ________________________ Chapter- 4 Triangle and Congruence Triangle Triangle A triangle Edges and vertices 3 Schläfli symbol {3} A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A , B , and C is denoted ABC . In Euclidean geometry any three non-collinear points determine a unique triangle and a unique plane (i.e. a two-dimensional Euclidean space). ________________________ WORLD TECHNOLOGIES ________________________ Types of triangles By relative lengths of sides Triangles can be classified according to the relative lengths of their sides: • In an equilateral triangle all sides have the same length. An equilateral triangle is also a regular polygon with all angles measuring 60°. • In an isosceles triangle , two sides are equal in length. An isosceles triangle also has two angles of the same measure; namely, the angles opposite to the two sides of the same length; this fact is the content of the Isosceles triangle theorem. Some mathematicians define an isosceles triangle to have exactly two equal sides, whereas others define an isosceles triangle as one with at least two equal sides. The latter definition would make all Equilateral Triangles isosceles triangles. • In a scalene triangle , all sides are unequal. The three angles are also all different in measure. Some (but not all) scalene triangles are also right triangles. . Equilateral Isosceles Scalene By internal angles Triangles can also be classified according to their internal angles, measured here in degrees. • A right triangle (or right-angled triangle , formerly called a rectangled triangle ) has one of its interior angles measuring 90° (a right angle). The side opposite to the right angle is the hypotenuse; it is the longest side of the right triangle. The other two sides are called the legs or catheti (singular: cathetus ) of the triangle. - eBook - PDF
Dr. Math Presents More Geometry
Learning Geometry is Easy! Just Ask Dr. Math
- (Author)
- 2005(Publication Date)
- Jossey-Bass(Publisher)
If I use this point as a center to draw a circle, what is the relation of this circle to the triangle? Please help me with the answer. Thank you. Yours truly, Quentin The Angle Bisectors of a Triangle B A C 3 3 You asked what happens if you use this point as the center of a cir- cle and how that circle is related to the triangle. You can draw lots of circles with their center at I, but the one that you’re probably most inter- ested in is the incircle, which is a circle centered at I that is tangent to all three sides of the triangle. —Dr. Math, The Math Forum Isosceles and Equilateral Triangles Isosceles and Equilateral Triangles have special properties, which means that we can figure out more about them than we might about a scalene triangle. An isosceles triangle has at least two equal sides. They’re usually called the legs, while the third side is called the base. The two base angles—those that include the base of the triangle—are equal. In an equilateral triangle, all of the sides and the angles are equal. An equilateral triangle is also an isosceles triangle, so every- thing that is true about isosceles triangles is also true of Equilateral Triangles. 62 Dr. Math Presents More Geometry I Dear Dr. Math, Given that one base angle of an isosceles triangle is 39 degrees, find the measure of the other two angles in the triangle. Yours truly, Qian Isosceles Triangles: Angles Hi, Qian, To start, let’s make sure you understand the definitions of the terms. An isosceles triangle has two congruent sides with a third side that is the base. A base angle of an isosceles triangle is one of the angles formed by the base and another side. Base angles are equal because of the definition of an isosceles triangle. A diagram would probably help here: ABC is an isosceles triangle. AB is congruent to AC. ∠ABC is con- gruent to ∠ACB. These are the base angles. Now let’s look at what we’re given and what we’re asked to find out. We’re given that one of the base angles is 39 degrees. - No longer available |Learn more
- Daniel C. Alexander, Geralyn M. Koeberlein, , , Daniel C. Alexander, Geralyn M. Koeberlein(Authors)
- 2014(Publication Date)
- Cengage Learning EMEA(Publisher)
All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. A Look Back at Chapter 3 In this chapter, we considered several methods for proving triangles congruent. We explored properties of isosceles triangles and justi-fied construction methods of earlier chapters. Inequality relation-ships for the sides and angles of a triangle were also investigated. A Look Ahead to Chapter 4 In the next chapter, we use properties of triangles to develop the prop-erties of quadrilaterals. We consider several special types of quadrilat-erals, including the parallelogram, kite, rhombus, and trapezoid. Key Concepts 3.1 Congruent Triangles • SSS, SAS, ASA, AAS • Included Side, Included Angle • Reflexive Property of Congruence (Identity) • Symmetric and Transitive Properties of Congruence 3.2 CPCTC • Hypotenuse and Legs of a Right Triangle • HL • Pythagorean Theorem • Square Roots Property Summary 162 CHAPTER 3 ■ TRIANGLES In algebra, it is shown that ; not by coincidence, the set which has 0 elements, has 1 subset. Just as , the set which has 1 element, has 2 subsets. The pattern continues so that a set with 2 elements has subsets and a set with 3 elements has subsets. A quick examination suggests this fact: The entries of the fifth row of Pascal’s Triangle correspond to the numbers of subsets of the four-element set ; of course, the subsets of must have 0 elements, 1 ele-ment each, 2 elements each, 3 elements each, or 4 elements each. Based upon the preceding principle, there will be a total of subsets for . EXAMPLE 1 List all 16 subsets of the set by considering the fifth row of Pascal’s Triangle, namely 1 4 6 4 1. - Alan Tussy, Diane Koenig(Authors)
- 2018(Publication Date)
- Cengage Learning EMEA(Publisher)
114° 6. 61.5° SECTION STUDY SET 9.3 Answers to Self Checks VOCABULARY Fill in the blanks. 1. A is a closed geometric figure with at least three line segments for its sides. 2. The polygon shown to the right has seven and seven vertices. 3. A point where two sides of a polygon intersect is called a of the polygon. 4. A polygon has sides that are all the same length and angles that all have the same measure. 5. A triangle with three sides of equal length is called an triangle. An triangle has at least two sides of equal length. A triangle has no sides of equal length. 6. An triangle has three acute angles. An triangle has one obtuse angle. A triangle has one right angle. 7. The longest side of a right triangle is called the . The other two sides of a right triangle are called . 8. The angles of an isosceles triangle have the same measure. The sides of equal length of an isosceles triangle form the angle. 9. In this section, we discussed the sum of the measures of the angles of a triangle. The word sum indicates the operation of . 10. Complete the table. Number of Sides Name of Polygon 3 4 5 6 7 8 9 10 12 CONCEPTS 11. Draw an example of each type of regular polygon. a. hexagon b. octagon c. quadrilateral d. triangle e. pentagon f. decagon 12. Refer to the triangle below. a. What are the names of the vertices of the triangle? b. How many sides does the triangle have? Name them. c. Use the vertices to name this triangle in three ways. H J I 13. Draw an example of each type of triangle. a. isosceles b. equilateral c. scalene d. obtuse e. right f. acute 14. Classify each triangle as an acute, an obtuse, or a right triangle. a. b. 90° c. d. 91° 15. Refer to the triangle shown to the right. a. What is the measure of H11028B? b. What type of triangle is it? c. What two line segments form the legs? d. What line segment is the hypotenuse? e. Which side of the triangle is the longest? f. Which side is opposite H11028B? A C B Copyright 2019 Cengage Learning.
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.