Physics
Non Linear Op Amp
A non-linear op amp is an operational amplifier whose output does not have a linear relationship with its input. In other words, the output voltage does not change in direct proportion to the input voltage. Non-linear op amps are often used in applications where precise control and manipulation of signals are required, such as in audio processing and instrumentation.
Written by Perlego with AI-assistance
Related key terms
1 of 5
10 Key excerpts on "Non Linear Op Amp"
- eBook - PDF
- G B Clayton(Author)
- 2013(Publication Date)
- Butterworth-Heinemann(Publisher)
CHAPTER FIVE NONLINEAR CIRCUITS In the basic amplifier circuits discussed in the previous chapter relation-ships between input and output signals are linear and independent of frequency, (at least over the range of frequencies of interest). Linear frequency independent relationships arise because of the use of linear resistors for input and feedback components. Nonlinear components give nonlinear relationships, reactive components give frequency dependent relationships. Nonlinear amplifiers find many applications in computation and signal processing. In such applications the functional relationship required between input and output can be arbitrary, or alternatively some definite mathematical function may be required, for example, e Q = e. 2 , c Q = sin e, e Q = log e ]m In particular a logarithmic conversion has many uses. Computing operations such as multiplication, division, and the taking of powers or roots may all be performed using logarith-mic amplifiers. Instrumentation systems, capable of accurately measur-ing both large and small signals on a single measurement channel, are sometimes required; in such cases a logarithmic amplifier provides a convenient method of compressing the wide range data. Conversely, an antilog relationship allows an expansion of narrow range data. 5.1 Amplifiers with defined nonlinearity Defined nonlinear amplification requires the use of a circuit element with a voltage-current characteristic exhibiting the desired nonlinearity. I -f ( e ) Nonlinear element e 0 =-Rf(e;) Figure 5.1 Operational amplifier with nonlinear input path 163 The element is connected as either the input or feedback path in an operational feedback circuit. In Figure 5.1 a nonlinear element is shown replacing the normal input resistor used in the inverting amplifier circuit. The usual summing point restraints applied to the circuit give Thus /j = f(e) and l = / f e Q = -Rf(e ] ) R i f — f M -Nonlinear element -* CZZ> « . - Dennis L. Eggleston(Author)
- 2011(Publication Date)
- Cambridge University Press(Publisher)
Also, the power supply connections shown in Fig. 6.1 are often omitted from circuit diagrams for simplicity, and it is easy for the novice building such a circuit to forget these connections. Of course, the circuit will not work without them. The basic operation of the op-amp can be simply stated. The output voltage is proportional to the difference between the inverting and non-inverting input voltages: V out = A OL ( V + in − V − in ) (6.1) 6.2 Non-linear applications I 153 V − in − + V + cc V − cc V out V + in Figure 6.1 Schematic symbol for the operational amplifier. where A OL is the open-loop voltage gain . Note that the plus and minus signs on the two input voltages are simply labels denoting which input the voltage is applied to; they do not specify the polarity of the input voltages. Typically, A OL is very large (for the 741 it is 200 000). One might then imagine huge output voltages, but Eq. (6.1) is subject to limitations. The output voltage V out can only be within a range set by two saturation voltages : V − sat ≤ V out ≤ V + sat (6.2) where V + sat ≈ V + cc − 1 V (a little below the positive power supply voltage) and V − sat ≈ V − cc + 1 V (a little above the negative power supply voltage). The output current is also restricted: for the 741 op-amp it must be less than 25 mA. Finally, we note that the input impedance of the two inputs is very high, so very little current flows into these inputs. The restrictions imposed by Eq. (6.2) along with the large value of A OL mean that any small difference between the op-amp inputs will cause the output to saturate. For example, if we use the 741 op-amp with ± 15 V power supplies, it takes only a 70 μ V difference between the inputs for the output to reach its limit. This is the basis for the non-linear applications of the op-amp. 6.2 Non-linear applications I Non-linear applications of the op-amp use the device as a comparator .- eBook - PDF
- Jiri Dostal(Author)
- 2013(Publication Date)
- Newnes(Publisher)
Parti The Operational Amplifier This page intentionally left blank 1. Basic Concepts 1.1 The Operational Amplifier The operational amplifier is a versatile amplifying device, originally intended for use in analog computers to perform linear mathematical operations. Forty years of development of the operational amplifier's internal circuit design reflects, to a significant extent, the development of electronic components from vacuum tubes to monolithic integrated circuits. An increasing refinement of the operational amplifier's properties has shifted the emphasis of its ap-plications from laboratories to industry. Due to its high performance, ver-satility, and low price, the operational amplifier now dominates the field of analog electronic systems. We generally define the operational amplifier as a direct-coupled amplifier with a high gain and a low level of inherent noise, capable of stable operation in a closed-feedback loop. The exact meaning of these characteristics will be given in Chapters 2 and 11. It should be mentioned here that the term direct-coupled does not imply an upper limitation of the amplifier's frequency re-sponse but, on the contrary, an extension of the operating range to zero frequency, or infinitely long periods. The direction of signal flow from input to output in an operational amplifier is given by the triangular shape of its symbol in Figure 1-la. Three of the four illustrated terminals represent the three signal terminals of an actual operational amplifier. These are the inverting input, noninverting input, and output. The fourth signal terminal, the ground, may be either actual (Figure 1—lb) or only virtual (power supply common in Figure 1-lc). In either case, it represents symbolically a group of at least two terminals intended for the supply of energy. - eBook - PDF
- Behzad Razavi(Author)
- 2021(Publication Date)
- Wiley(Publisher)
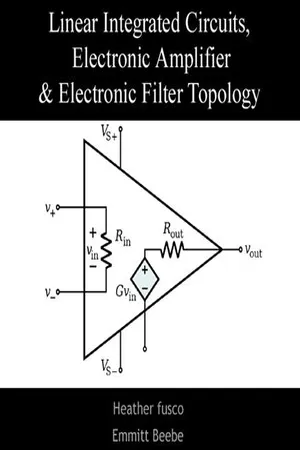
In this chapter, we study the operational amplifier as a black box, developing op-amp-based circuits that perform interesting and useful functions. The outline is shown below. 1 Vacuum tubes were amplifying devices consisting of a filament that released electrons, a plate that collected them, and another that controlled the flow—somewhat similar to MOSFETs. 355 356 Chapter 8 Operational Amplifier as a Black Box General Concepts • Op Amp Properties Linear Op Amp Circuits • Noninverting Amplifier • Inverting Amplifier • Integrator and Differentiator • Voltage Adder Nonlinear Op Amp Circuits • Precision Rectifier • Logarithmic Amplifier • Square Root Circuit Op Amp Nonidealities • DC Offsets • Input Bias Currents • Speed Limitations • Finite Input and Output Impedances 8.1 GENERAL CONSIDERATIONS The operational amplifier can be abstracted as a black box having two inputs and one output. 2 Shown in Fig. 8.1(a), the op amp symbol distinguishes between the two inputs by the plus and minus sign; V in1 and V in2 are called the “noninverting” and “inverting” inputs, respectively. We view the op amp as a circuit that amplifies the difference between the two inputs, arriving at the equivalent circuit depicted in Fig. 8.1(b). The voltage gain is denoted by A 0 : V out = A 0 (V in1 − V in2 ). (8.1) We call A 0 the “open-loop” gain. V V in1 in2 out V in1 in2 A 0 V V in1 V ( V in2 – out V (a) (b) ) Figure 8.1 (a) Op amp symbol, (b) equivalent circuit. It is instructive to plot V out as a function of one input while the other remains at zero. With V in2 = 0, we have V out = A 0 V in1 , obtaining the behavior shown in Fig. 8.2(a). The positive slope (gain) is consistent with the label “noninverting” given to V in1 . On the other hand, if V in1 = 0, V out = −A 0 V in2 [Fig. 8.2(b)], revealing a negative slope and hence an “inverting” behavior. - eBook - ePub
Introduction to Energy, Renewable Energy and Electrical Engineering
Essentials for Engineering Science (STEM) Professionals and Students
- Ewald F. Fuchs, Heidi A. Fuchs(Authors)
- 2020(Publication Date)
- Wiley(Publisher)
8 Operational Amplifiers8.1 Introduction
The operational (OP) amplifier is a basic building block for the design of analog electronic systems such as feedback control circuits [1 ], where the angular velocity ω m (t), angular position θ m (t) = ∫ω m (t)dt, current i(t), and torque T(t) must be controlled. An OP amplifier with no external circuitry is a voltage amplifier with a very high open‐loop voltage gain that ideally approaches infinity A v → ∞, as shown in a symbolic manner in Figure 8.1 . Note that input/output voltages can be either time varying or time independent, and they can be either periodic or nonperiodic.OP amplifiers are integrated circuits (IC), which can be purchased off the shelf, and they contain transistors, diodes, resistors, and capacitors all fabricated on a single silicon chip. Inductors are bulky and are mostly avoided in OP amplifier designs. The analog electronic circuit of Figure 8.1 has two inputs: a negative (v − ) and a positive (v + ) input supplied by the voltages v in1 and v in2 , respectively, whose difference in voltage (v in2 − v in1 ) produces an output signal voltage v out that is a replica of the input voltage difference. The two‐input voltage approach is useful because stray signals/electric noise that appear on both inputs are cancelled, and only the voltage difference is amplified. An OP amplifier is also called a differential amplifier because the output voltage is a voltage that is A v times the voltage difference between the two inputs. During the past half century, OP amplifiers have been refined and improved to the extent that they have nearly ideal properties, and therefore we discuss in this textbook the performance of ideal OP amplifiers only. The understanding of nonideal properties of OP amplifiers requires detailed electronic knowledge [2 - eBook - ePub
- John E. Ayers(Author)
- 2024(Publication Date)
- CRC Press(Publisher)
3 Operational Amplifier CircuitsDOI: 10.1201/9781003408529-33.1 Introduction to Operational Amplifiers
The operational amplifier (op amp) is an electronic differential amplifier with two inputs and one output as shown in Figure 3.1 . Although a typical op amp contains a large number of transistors and resistors, our focus will be on the external circuit behavior. This external behavior may be readily understood by the use of Kirchhoff’s and Ohm’s laws because commercially available op amps have nearly ideal behavior in many respects.Long Description for Figure 3.1Schematic symbol for an operational amplifier, including the two input terminals, the output terminal, and the two power supply terminals. The symbol is an isosceles triangle with the short side on the left and the point on the right. The noninverting input is on the top of the left side, and marked by a plus sign. The voltage at this terminal is labeled Vp and the current entering this terminal is labeled ip. The inverting input is at the bottom of the left side, and is marked by a minus sign. The voltage at this terminal is labeled Vn and the current entering this terminal is labeled in. At the point of the triangle on the right hand side is the output terminal, which is labeled Vout. On the sloping top of the triangle is the positive supply terminal, labeled +VCC, and on the sloping bottom of the triangle is the negative terminal, labeled –VEE.FIGURE 3.1 Operational amplifier symbol with power connections.The op amp is a differential amplifier and therefore amplifies the difference between two input voltages. Referring to Figure 3.1 , the input terminal marked with a plus sign is the non-inverting input with the voltagev papplied, and the input terminal marked with a minus sign is the inverting input with the voltagev napplied. The input currentsi pandi nflow into the non-inverting and inverting terminals, respectively. For a real op amp, these currents are so small that they may usually be neglected. The output terminal emanates from the point of the triangular symbol, and the voltage at this terminal isV out. The other two terminals shown on the op amp are the power terminals; the positive supply is+and the negative supply isVC C−VE E - eBook - PDF
- Richard C. Dorf, James A. Svoboda(Authors)
- 2020(Publication Date)
- Wiley(Publisher)
6 The Operational Ampli fier Chapter Topics 6.1 Introduction 6.2 The Operational Amplifier 6.3 The Ideal Operational Amplifier 6.4 Nodal Analysis of Circuits Containing Ideal Operational Amplifiers 6.5 Design Using Operational Amplifiers 6.6 Operational Amplifier Circuits and Linear Algebraic Equations 6.7 Characteristics of Practical Operational Amplifiers 6.8 Analysis of Op Amp Circuits Using MATLAB 6.9 Using PSpice to Analyze Op Amp Circuits 6.10 How Can We Check . . . ? 6.11 DESIGN EXAMPLE— Transducer Interface Circuit 6.12 Summary Problems PSpice Problems Design Problems 6.1 I n t r o d u c t i o n This chapter introduces another circuit element, the operational amplifier, or op amp. We will learn how to analyze and design electric circuits that contain op amps. In particular, we will see that: Several models, of varying accuracy and complexity, are available for operational amplifiers. Simple models are easy to use. Accurate models are more complicated. The simplest model of the operational amplifier is the ideal operational amplifier. Circuits that contain ideal operational amplifiers are analyzed by writing and solving node equations. Operational amplifiers can be used to build circuits that perform mathematical operations. Many of these circuits are widely used and have been named. Figure 6.5-1 provides a catalog of some useful operational amplifier circuits. Practical operational amplifiers have properties that are not included in the ideal operational amplifier. These include the input offset voltage, bias current, dc gain, input resistance, and output resistance. More complicated models are needed to account for these properties. 6.2 T h e O p e r a t i o n a l A m p l i f i e r The operational amplifier is an electronic circuit element designed to be used with other circuit elements to perform a specified signal-processing operation. The mA741 operational amplifier is shown in Figure 6.2-1a. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- College Publishing House(Publisher)
In the first approximation op-amps can be used as if they were ideal differential gain blocks; at a later stage limits can be placed on the acceptable range of parameters for each op-amp. Circuit design follows the same lines for all electronic circuits. A specification is drawn up governing what the circuit is required to do, with allowable limits. For example, the gain may be required to be 100 times, with a tolerance of 5% but drift of less than 1% in a specified temperature range; the input impedance not less than one megohm; etc. A basic circuit is designed, often with the help of circuit modeling (on a computer). Specific commercially available op-amps and other components are then chosen that meet the design criteria within the specified tolerances at acceptable cost. If not all criteria can be met, the specification may need to be modified. A prototype is then built and tested; changes to meet or improve the specification, alter functionality, or reduce the cost, may be made. ____________________ WORLD TECHNOLOGIES ____________________ Basic single stage amplifiers Non-inverting amplifier An op-amp connected in the non-inverting amplifier configuration In a non-inverting amplifier, the output voltage changes in the same direction as the input voltage. The gain equation for the op-amp is: However, in this circuit V – is a function of V out because of the negative feedback through the R 1 R 2 network. R 1 and R 2 form a voltage divider, and as V – is a high-impedance input, it does not load it appreciably. Consequently: where Substituting this into the gain equation, we obtain: Solving for V out : If A OL is very large, this simplifies to ____________________ WORLD TECHNOLOGIES ____________________ . Inverting amplifier An op-amp connected in the inverting amplifier configuration In an inverting amplifier, the output voltage changes in an opposite direction to the input voltage. - No longer available |Learn more
- (Author)
- 2014(Publication Date)
- Academic Studio(Publisher)
In the first approximation op-amps can be used as if they were ideal differential gain blocks; at a later stage limits can be placed on the acceptable range of parameters for each op-amp. Circuit design follows the same lines for all electronic circuits. A specification is drawn up governing what the circuit is required to do, with allowable limits. For example, the gain may be required to be 100 times, with a tolerance of 5% but drift of less than 1% in a specified temperature range; the input impedance not less than one megohm; etc. A basic circuit is designed, often with the help of circuit modeling (on a computer). Specific commercially available op-amps and other components are then chosen that meet the design criteria within the specified tolerances at acceptable cost. If not all criteria can be met, the specification may need to be modified. A prototype is then built and tested; changes to meet or improve the specification, alter functionality, or reduce the cost, may be made. ____________________ WORLD TECHNOLOGIES ____________________ Basic single stage amplifiers Non-inverting amplifier An op-amp connected in the non-inverting amplifier configuration In a non-inverting amplifier, the output voltage changes in the same direction as the input voltage. The gain equation for the op-amp is: However, in this circuit V – is a function of V out because of the negative feedback through the R 1 R 2 network. R 1 and R 2 form a voltage divider, and as V – is a high-impedance input, it does not load it appreciably. Consequently: where Substituting this into the gain equation, we obtain: Solving for V out : If A OL is very large, this simplifies to . ____________________ WORLD TECHNOLOGIES ____________________ Inverting amplifier An op-amp connected in the inverting amplifier configuration In an inverting amplifier, the output voltage changes in an opposite direction to the input voltage. - eBook - PDF
Fundamentals of Electronics
Book 1 Electronic Devices and Circuit Applications
- Thomas F. Schubert, Ernest M. Kim(Authors)
- 2022(Publication Date)
- Springer(Publisher)
1 C H A P T E R 1 Operational Amplifiers and Applications e Operational Amplifier (commonly referred to as the OpAmp) is one of the primary active devices used to design low and intermediate frequency analog electronic circuitry: its importance is surpassed only by the transistor. OpAmps have gained wide acceptance as electronic building blocks that are useful, predictable, and economical. Understanding OpAmp operation is funda- mental to the study of electronics. e name, operational amplifier, is derived from the ease with which this fundamental building block can be configured, with the addition of minimal external circuitry, to perform a wide variety of linear and non-linear circuit functions. Originally implemented with vacuum tubes and now as small, transistorized integrated circuits, OpAmps can be found in applications such as: signal processors (filters, limiters, synthesizers, etc.), communication circuits (oscillators, modulators, demodulators, phase-locked loops, etc.), Analog/Digital converters (both A to D and D to A), and circuitry performing a variety of mathematical operations (multipliers, dividers, adders, etc.). e study of OpAmps as circuit building blocks is an excellent starting point in the study of electronics. e art of electronics circuit and system design and analysis is founded on circuit realizations created by interfacing building block elements that have specific terminal character- istics. OpAmps, with near-ideal behavior and electrically good interconnection properties, are relatively simple to describe as circuit building blocks. Circuit building blocks, such as the OpAmp, are primarily described by their terminal char- acteristics. Often this level of modeling complexity is sufficient and appropriately uncomplicated for electronic circuit design and analysis. However, it is often necessary to increase the complexity of the model to simplify the analysis and design procedures.
Index pages curate the most relevant extracts from our library of academic textbooks. They’ve been created using an in-house natural language model (NLM), each adding context and meaning to key research topics.