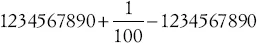Gli errori nelle dimostrazioni matematiche

Imparare la matematica e la logica dagli errori (degli altri)

Paolo Pietro Lava, Giorgio Balzarotti

• Editore: Hoepli
• Anno: 2013
• ISBN:
  9788820358051
• Argomento: Psicologia
• Categoria: Scienze cognitive

Una dimostrazione non è necessariamente corretta soltanto perché le conseguenze sono giuste o ragionevoli; al contrario, errori nel ragionamento logico-matematico possono portare a risultati paradossali.Gli autori hanno raccolto in questo volume una serie di dimostrazioni in cui evidenziano, attraverso un percorso elementare ma esauriente, tale genere di errori.Alcuni capitoli presentano i tipici errori in cui si può incorrere con una non oculata applicazione delle regole dell'algebra e della geometria e con l'errata generalizzazione di proprietà particolari. Altri capitoli sviluppano il tema degli errori provenienti da una non chiara e precisa definizione delle regole e dall'uso di concetti solo apparentemente evidenti. Altri ancora affrontano la critica questione della ripetizione infinita di proprietà o regole elementari e dei paradossi che ne possono derivare.Gli errori dovuti all'incompletezza delle definizioni e delle regole permettono, poi, di introdurre le difficili tematiche attinenti alla logica della dimostrazione. Alcuni esempi, infine, affrontano le conseguenze dell'applicazione di inadeguati modelli matematici al mondo fisico.

Capitolo 1

Tutti i numeri sono uguali al loro doppio

Si vuole dimostrare che:

a = 2a

per ogni a non necessariamente nullo.

Presi due numeri qualunque a e b tali che:

a = b

si moltiplichino entrambi i termini dell’uguaglianza per a, ottenendo:

a² = ab

Sottraendo a entrambi i membri b², continuerà a valere anche l’uguaglianza:

a² – b² = ab – b²

Ricordando che la differenza di due quadrati è pari al prodotto della somma delle basi per la loro differenza, si ha:

(a + b) (a – b) = ab – b²

Raccogliendo b tra i termini di destra, possiamo scrivere:

(a + b) (a – b) = b(a – b)

Semplificando i termini dell’uguaglianza:

(a + b) (a – b) = b(a – b)

(a + b) = b

Dato che, per l’ipotesi iniziale, a = b, è possibile sostituire a a b nell’uguaglianza ottenendo:

2a = a

che è quanto ci si era prefissati di dimostrare.

Questo risultato, inverosimile, è stato ottenuto perché non si sono rispettate le “regole del gioco”. Ogni passaggio o operazione, anche in una dimostrazione semplice come quella illustrata, ha delle regole, che non possono essere cambiate a piacimento, ignorate o adottate solo parzialmente.

È facile individuare l’errore nella semplice dimostrazione proposta, ma affrontiamo il problema in modo metodico.

La dimostrazione inizia con l’affermazione: “presi due numeri qualunque a e b...”. Si parta quindi dall’insieme di numeri (indicato con I nella figura) e dalla possibilità di scegliere due elementi qualunque.

Nei passaggi successivi della dimostrazione, sono state utilizzate le quattro operazione elementari, addizione, moltiplicazione e le loro operazioni inverse, sottrazione e divisione.

Sono state considerate valide anche alcune proprietà elementari di tali operazioni: la proprietà commutativa e quella associativa. Non si è posto vincoli sul loro uso e non tutte, comunque, sono state applicate direttamente. Quindi si è applicata la proprietà distributiva della moltiplicazione rispetto l’addizione.

Si è ipotizzato che le operazioni applicate fossero tutte interne all’insieme, cioè che il risultato dell’applicazione di una di esse su due elementi dell’insieme fosse ancora un elemento dell’insieme stesso.

La prima obiezione, a quanto ipotizzato o sottinteso, nasce dall’uso incondizionato della sottrazione. Avremmo dovuto porre una condizione sulle caratteristiche dell’insieme I sottolineando che non si trattava dell’insieme dei naturali, o precisare un limite sull’applicabilità della sottrazione agli elementi dell’insieme. Infatti, la sottrazione non è un’operazione interna all’insieme dei numeri naturali perché sottraendo un numero qualunque a un altro qualunque, il risultato potrebbe essere un numero negativo, che non appartiene all’insieme dei numeri naturali. Avremmo dovuto quindi porre una condizione sulle caratteristiche dell’insieme I o all’applicabilità di tale operazione sugli elementi dell’insieme dei naturali.

Nella sottrazione dei due numeri avremmo dovuto supporre anche la presenza dell’elemento neutro (lo zero), cosa non vera in generale, per convenzione, nell’insieme dei naturali.

Nel prodotto d’entrambi i membri dell’eguaglianza per a, abbiamo sottinteso valida la proprietà commutativa, infatti abbiamo scritto:

a² = ab

senza preoccuparci di scrivere, eventualmente, invertendo l’ordine dei fattori:

a² = ba

Abbiamo anche scritto, sempre supponendo valida la proprietà commutativa:

(a + b) (a – b) = b(a – b)

invece di:

(a – b) (a + b) = b(a – b)

Implicitamente abbiamo ipotizzato di operare con un insieme di numeri e con delle operazioni senza nessun vincolo.

Semplifichiamo tutte queste considerazioni supponendo che l’insieme dei numeri, da cui sono stati scelti i due elementi, sia l’insieme dei reali dove sappiamo valere tutte le ipotesi sopra indicate. Utilizziamo quindi l’insieme dei numeri reali, anche se questo non è strettamente necessario per la dimostrazione.

Con questa scelta non sono stati però risolti tutti i problemi. Il principale nasce dall’applicazione della divisione. La divisione, infatti, non è un’operazione interna all’insieme dei reali perché non è possibile in generale dividere un elemento qualunque per un altro qualunque. L’insieme è chiuso rispetto a tale operazione solo se si toglie lo zero.

È questa la “regola del gioco” che abbiamo ignorato nella dimostrazione:

la divisione non poteva essere applicata senza una verifica sul divisore.

In un certo punto, nella dimostrazione, abbiamo diviso entrambi i termini dell’eguaglianza per zero. Dividendo impropriamente per zero l’uguaglianza 0·(a + b) = 0·b, ottenendo in questo modo (a + b) = b, abbiamo posto uguali due numeri qualunque.

L’errore era facilmente “scovabile” nei pochi passaggi di questa dimostrazione. È un errore in cui gli studenti dei primi anni delle scuole superiori possono facilmente incorrere ma, se lo pensiamo immerso in pagine e pagine di calcoli e di espressioni letterali, potrebbe sfuggire anche a osservatori più esperti. Tanto che Bernard Bolzano, scrivendo il suo I paradossi dell’infinito nel 1848, menziona tale errore come diffuso ai suoi tempi. Non si portino, però, a spiegazione dell’errore della nostra dimostrazione, concetti di infinito. Ci preme particolarmente sottolineare questo punto per una correttezza di ragionanento. Poiché, senza molto formalismo, ma con molta efficacia, si usa comunemente dire che dividendo per zero un numero qualunque diverso da zero si ha infinito e che, moltiplicando un numero qualunque per infinito, il risultato è comunque infinito, l’errore nella nostra dimostrazione potrebbe essere analizzato sulla base di tali concetti.

Bernard Bolzano (1781-1848)

Matematico e filosofo di origine italiana, nato e morto a Praga. Fu per anni professore di Filosofia della religione a Praga. Si dedicò alla logica, alla matematica, alla filosofia, alla fisica e alla sociologia. Purtroppo Bolzano ha avuto un limitato impatto sull’analisi matematica moderna poiché la maggior parte dei suoi scritti rimase inedita e dimenticata per decenni, nonostante l’elevato rigore e il profondo contenuto innovativo rispetto a quello dei contemporanei.

In realtà:

il problema risiede solamente nell’aver ignorato le proprietà delle operazioni definite sull’insieme dei numeri reali,

e non è necessario o, meglio ancora, non è appropriato introdurre in modo forzato il concetto di infinito.

Approfittiamo per affrontare una tematica affine: è importante ricordare che, a causa delle approssimazioni nel calcolo numerico con calcolatori elettronici, la divisione con numeri piccoli deve essere gestita con cura, perché potrebbe portare a grossolani errori nei risultati. Nei programmi al calcolatore, ricordatevi di porre delle condizioni sul divisore e, all’occorrenza, su tutte le operazioni con numeri piccoli. Gestite il calcolo con una procedura specifica anche perché il numero totale delle cifre utilizzate da un calcolatore è limitato e potrebbe non essere sufficiente alle vostre necessità.

Si consideri, a questo scopo, il seguente esempio. Mediante una calcolatrice tascabile, con display a 10 cifre, si effettuino queste operazioni in successione:

quindi si moltiplichi il risultato per 100. Il nostro calcolatore tascabile fornirà uno 0 mentre è evidente, effettuando le semplificazioni con carta e penna, che il risultato, al contrario, è 1.

Approfondimenti

L’insieme di elementi e le operazioni interne sugli elementi formano le strutture algebriche. Con altri numeri e con altre proprietà avremmo potuto realizzare altre dimostrazioni paradossali, per esempio ignorando l’ordine dei fattori in strutture algebriche dove non vale la proprietà commutativa. Poiché il concetto di struttura algebrica non è molto utilizzato e non ha neppure molta utilità nelle applicazioni dei non professionisti della matematica, è anche uno degli argomenti di studio che è più frequentemente dimenticato. Facciamo un breve ripasso perché riteniamo che le strutture algebriche abbiano una notevole importanza dal punto di vista della metodologia necessaria per affrontare i problemi. Nomenclatura e definizioni, che spesso nella letteratura matematica non son...