Elementary Statistical Physics

Charles Kittel

• Publisher: Dover Publications
• Year: 2012
• Print ISBN: 9780486435145
• eBook ISBN: 9780486138909
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

Noteworthy for the philosophical subtlety of its foundations and the elegance of its problem-solving methods, statistical mechanics can be employed in a broad range of applications — among them, astrophysics, biology, chemistry, nuclear and solid state physics, communications engineering, metallurgy, and mathematics. Geared toward graduate students in physics, this text covers such important topics as stochastic processes and transport theory in order to provide students with a working knowledge of statistical mechanics.
To explain the fundamentals of his subject, the author uses the method of ensembles developed by J. Willard Gibbs. Topics include the properties of the Fermi-Dirac and Bose-Einstein distributions; the interrelated subjects of fluctuations, thermal noise, and Brownian movement; and the thermodynamics of irreversible processes.
Negative temperature, magnetic energy, density matrix methods, and the Kramers-Kronig causality relations are treated briefly. Most sections include illustrative problems. Appendix. 28 figures. 1 table.

part 1.

Fundamental principles of statistical mechanics

1. Review of Classical Mechanics

Reference:

H. Goldstein, Classical mechanics, Addison-Wesley, Cambridge, Mass., 1953, Chap. 7.

The subject of classical statistical mechanics may be developed most naturally in terms of the conjugate coordinate and momentum variables q_i and p_i which are used in the classical equations of motion in the Hamiltonian form. The reason for working with coordinates and momenta, rather than coordinates and velocities, will appear when we discuss the Liouville theorem in Sec. 3 below. We now remind the reader of the definitions of the conjugate coordinate and momentum variables and of the content of the Hamilton equations.

We consider a conservative classical system with f degrees of freedom. For N point particles, f will be equal to 3N. We suppose that we have a set of generalized coordinates for the system:

These may be Cartesian, polar, or some other convenient set of coordinates. The generalized velocities associated with these coordinates are

The expression of Newton’s second law by the Lagrangian equations of motion is

where for a simple non-relativistic system the Lagrangian L is given by

Here T is the kinetic energy and V is the potential energy. Equation (1.1) is easily verified if the q_i are Cartesian coordinates, for then we have

and, letting q_i = x,

but −∂V/∂x is just the x component of the force F, and we have simply

The Hamiltonian form of the equations of motion replaces the f second-order differential equations (1.1) by 2f first-order differential equations. We define the generalized momenta by

The Hamiltonian

is defined as

Then

The terms in d

_i cancel by the definition (1.6) of the p_i. Further, from the Lagrange equations (1.1) we see that

Thus, from (1.8), we must have

These are the Hamilton equations of motion.

Example 1.1. We consider the motion of a classical harmonic oscillator in one dimension. The kinetic energy is

The potential energy will be written as

The Lagrangian is, from (1.2),

The Lagrangian equation of motion is, from (1.1),

which describes a periodic motion with angular frequency ω.

The generalized momentum is, from (1.6),

The Hamiltonian is, from (1.7),

where q ≡ x. The Hamilton equations of motion are, from (1.10),

which only confirms the definition of p, and

in agreement with the Lagrangian equation (1.14).

Example 1.2. We consider the ...

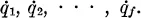
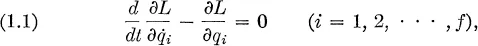
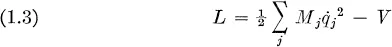
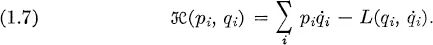
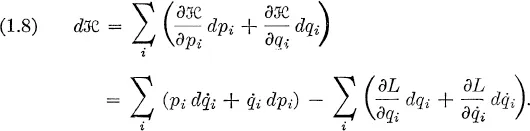
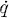
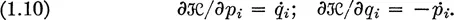
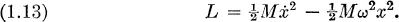
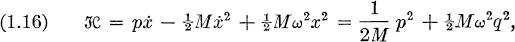
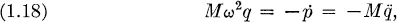
Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• part 1. Fundamental Principles of Statistical Mechanics
• part 2. Fluctuations, Noise, and Irreversible Thermodynamics
• part 3. Kinetic Methods and Transport Theory
• Appendix