Group Theory and Quantum Mechanics

Michael Tinkham

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486131665
• Topic: Physical Sciences
• Subtopic: Chemistry
• Index: Chemistry

This graduate-level text develops the aspects of group theory most relevant to physics and chemistry (such as the theory of representations) and illustrates their applications to quantum mechanics. The first five chapters focus chiefly on the introduction of methods, illustrated by physical examples, and the final three chapters offer a systematic treatment of the quantum theory of atoms, molecules, and solids.
The formal theory of finite groups and their representation is developed in Chapters 1 through 4 and illustrated by examples from the crystallographic point groups basic to solid-state and molecular theory. Chapter 5 is devoted to the theory of systems with full rotational symmetry, Chapter 6 to the systematic presentation of atomic structure, and Chapter 7 to molecular quantum mechanics. Chapter 8, which deals with solid-state physics, treats electronic energy band theory and magnetic crystal symmetry. A compact and worthwhile compilation of the scattered material on standard methods, this volume presumes a basic understanding of quantum theory.

FULL ROTATION GROUP
AND ANGULAR
MOMENTUM

5–1Rotational Transformation Properties and Angular Momentum

Before developing the representations of the full three-dimensional rotation group, let us review the underlying relation between the rotational transformation properties of a wavefunction and its angular momentum.

The linear momentum p of a system may be defined most basically as that quantity whose conservation is a consequence of the translational isotropy of space. Now, the isotropy of space means that the spatial gradient of the Hamiltonian H is zero and hence that ∇ commutes with H. But commutation of an operator with H is the requirement for conservation of that operator in quantum mechanics. Hence we associate ∇ with p and are led to the usual Schrödinger operator replacement p = (h/i)∇.

Considering for simplicity only the x component, we have

where P_δx is the transformation operator which shifts the contours of ψ(x) by δx with respect to fixed axes (or shifts the axes by −δx if the function is considered to be stationary). An alternative way of writing this equation is

where δx is treated as infinitesimal. These equations state the relationship between the linear-momentum operator and the transformation operator P_δx for translational displacement.

In a similar manner, we may define the x component of the angular momentum as the operator whose conservation follows from the invariance of the Hamiltonian under rotations about the x axis, i.e., from ∂H/∂θ_x = 0. In complete analogy to the linear momentum, we then obtain a definition of angular momentum in terms of infinitesimal rotations,

or

where P_δθx is the transformation operator which rotates the contours of the function by δθ_x about the x axis in the sense which makes a right-hand-screw advance along x. From this definition we can readily find the transformation operator Pθ_x for a finite rotation as follows: Let θ_x = n(δθ_x), and let n → ∞ while (δθ_x) → 0 in such a way as to hold θ_x constant. Then we can write P_θx as the result of n = θ_x/δθ_x iterations of P_δθx,

or

where we have used the definition of the exponential e^y as the limit of (1 + x)^y/x as x → 0. The second form (5–3b) indicates how one could go about calculation with an exponential operator by Taylor’s-series expansion. Clearly a result analogous to (5–3) is true for rotations about any axis, since we have made no special assumptions about the x axis. We have already made use of this result for the z component of the angular momentum in Sec. 4–4 while working out the character of the representations based on the spherical harmonics. Since the z axis was chosen for the axis of quantization, J_z had a definite value mh and we simply found

Note that this result follows directly from the relation between J_z and infinitesimal rotations. Hence it is valid whenever J_z is quantized. In particular, it holds also for half-integral j values where the spherical harmonics no longer serve as basis functions. This observation justifies our use of the formula (4–11) for the character χ_j(α) for half-integral as well as integral values of j. The double-valued characters noted there are consequences of the fact that, for half-integral j values, P_2πΨ_m^(j) = −ψ_m^(j), so that a rotation by 2π leaves the wavefunctions changed in phase.

We can use (5–3) to define the t...

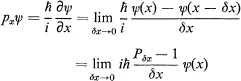
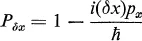
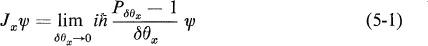
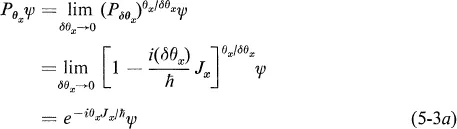
Table of contents

• Cover
• Title Page
• Copyright Page
• Preface
• Contents
• I Introduction
• 2 Abstract Group Theory
• 3 Theory of Group Representations
• 4 Physical Applications of Group Theory
• 5 Full Rotation Group and Angular Momentum
• 6 Quantum Mechanics of Atoms
• 7 Molecular Quantum Mechanics
• 8 Solid-state Theory
• Appendix
• Index