Representation Theory of Finite Groups

Martin Burrow

• Publisher: Dover Publications
• Year: 2014
• eBook ISBN: 9780486145075
• Topic: Mathematics
• Subtopic: Group Theory
• Index: Mathematics

This volume contains a concise exposition of the theory of finite groups, including the theory of modular representations. The rudiments of linear algebra and knowledge of the elementary concepts of group theory are useful, if not entirely indispensable, prerequisites for reading this book; most of the other requisites, such as the theory of p-adic fields, are developed in the text.
After an introductory chapter on group characters, repression modules, applications of ideas and results from group theory and the regular representation, the author offers penetrating discussions of the representation theory of rings with identity, the representation theory of finite groups, applications of the theory of characters, construction of irreducible representations and modular representations. Well-chosen exercises are included throughout to help students test their understanding of the material. An appendix on groups, rings, ideals, and fields, as well as a bibliography, round out this useful well-thought-out text.
Graduate students wishing to acquire some knowledge of representation theory will find this an excellent text for self-study. The book also lends itself to use as supplementary reading for a course in group theory or in the applications of representation theory to physics.

CHAPTER I

Foundations

1. Introduction

Nowadays it is natural for us to think of a group abstractly as a set of elements {a, b, c, ...}, which is closed under an associative multiplication and which permits a solution, for x and y, of any equations: ax = b, and ya = b. On the other hand, we regard a group, which is given in some concrete way, as a realization of an abstract group. This point of view is an inversion of the historical development of group theory which won the abstract concept from particular modes of representation.

Group theory began with finite permutation groups. Any arrangement of n objects in a row is called a permutation of the objects. If we select some arrangement as standard, then any other arrangement can be regarded as achieved from it by an operation of replacements: each object in the standard being replaced by that object which takes its place in the new arrangement. Thus if 123 is standard and 312 is another arrangement, then the replacements are 1 → 3, 2 → 1, and 3 → 2. We write compactly for this operation

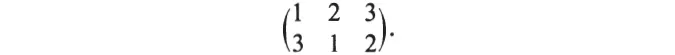
If the replacements of two operations are performed in succession, we get an arrangement which could be achieved directly by a third operation, called the product of the two operations. For example,

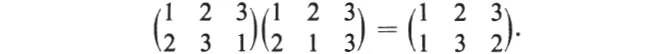
Here we have proceeded from left to right. The product of operations is associative and any set of operations which form a group is a permutation group.

If we have n objects 1, 2, ..., n, then there are n! arrangements and hence n! operations are possible, including the identity:

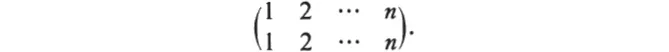
They form a group S_n, the symmetric group on n symbols. Every permutation group on n symbols is a subgroup of S_n. In a remarkable application of a group theory in its infancy Galois showed that every algebraic equation possesses a certain permutation group on whose structure its properties depend.

Cayley discovered the abstract group concept. A theorem of his asserts that every abstract group with a finite number of elements can be realized as a group of permutations of its elements. Thus if G = {a, b, c, ..., g, ...} is the abstract group, then the element of the permutation group P which corresponds to g is the set of replacements a → ag, b → bg, c → cg, ..., or compactly:

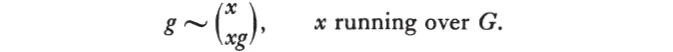
The groups G and P are isomorphic (see Appendix).

A generalization of the permutation group, and the next step historically, is the group of linear substitutions on a finite number of variables. In this case, if the variables are x₁, ...,...

Table of contents

• Cover
• Title Page
• Dedication
• Copyright Page
• Preface
• Contents
• Chapter I. Foundations
• Chapter II. Representation Theory of Rings with Identity
• Chapter III. The Representation Theory of Finite Groups
• Chapter IV. Applications of the Theory of Characters
• Chapter V. The Construction of Irreducible Representations
• Chapter VI. Modular Representations
• Appendix
• BIBLIOGRAPHY
• SUBJECT INDEX