Regular Polytopes

H. S. M. Coxeter

• Publisher: Dover Publications
• Year: 2012
• ISBN:
  9780486141589
• Topic: Matematica
• Subtopic: Geometria

Polytopes are geometrical figures bounded by portions of lines, planes, or hyperplanes. In plane (two dimensional) geometry, they are known as polygons and comprise such figures as triangles, squares, pentagons, etc. In solid (three dimensional) geometry they are known as polyhedra and include such figures as tetrahedra (a type of pyramid), cubes, icosahedra, and many more; the possibilities, in fact, are infinite! H. S. M. Coxeter's book is the foremost book available on regular polyhedra, incorporating not only the ancient Greek work on the subject, but also the vast amount of information that has been accumulated on them since, especially in the last hundred years. The author, professor of Mathematics, University of Toronto, has contributed much valuable work himself on polytopes and is a well-known authority on them.
Professor Coxeter begins with the fundamental concepts of plane and solid geometry and then moves on to multi-dimensionality. Among the many subjects covered are Euler's formula, rotation groups, star-polyhedra, truncation, forms, vectors, coordinates, kaleidoscopes, Petrie polygons, sections and projections, and star-polytopes. Each chapter ends with a historical summary showing when and how the information contained therein was discovered. Numerous figures and examples and the author's lucid explanations also help to make the text readily comprehensible.

Although the study of polytopes does have some practical applications to mineralogy, architecture, linear programming, and other areas, most people enjoy contemplating these figures simply because their symmetrical shapes have an aesthetic appeal. But whatever the reasons, anyone with an elementary knowledge of geometry and trigonometry will find this one of the best source books available on this fascinating study.

CHAPTER I

POLYGONS AND POLYHEDRA

TWO-DIMENSIONAL polytopes are merely polygons ; these are treated in § 1·1. Three-dimensional polytopes are polyhedra ; these are defined in § 1·2 and developed throughout the first six chapters. § 1·3 contains a version of Euclid’s proof that there cannot be more than five regular solids, and a simple construction to show that each of the five actually exists. The rest of Chapter I is mainly topological : a regular polyhedron is regarded as a map, and later as a configuration. In § 1·5 we take an excursion into “ recreational ” mathematics, as a preparation for the notion of a tree of edges in von Staudt’s elegant proof of Euler’s Formula.

1·1. Regular polygons. Everyone is acquainted with some of the regular polygons : the equilateral triangle which Euclid constructs in his first proposition, the square which confronts us all over the civilized world, the pentagon which can be obtained by making a simple knot in a strip of paper and pressing it carefully flat,³ the hexagon of the snowflake, and so on. The pentagon and the enneagon have been used as bases for the plans of two American buildings : the Pentagon Building near Washington, and the Bahá’í Temple near Chicago. Dodecagonal coins have been made in England and Canada.

To be precise, we define a p-gon as a circuit of p line-segments A₁ A₂, A₂ A₃, . . . , A_p A₁, joining consecutive pairs of p points A₁, A₂, . . . , Ap. The segments and points are called sides and vertices. Until we come to Chapter VI we shall insist that the sides do not cross one another. If the vertices are all coplanar we speak of a plane polygon, otherwise a skew polygon.

A plane polygon decomposes its plane into two regions, one of which, called the interior, is finite. We shall often find it convenient to regard the p-gon as consisting of its interior as well as its sides and vertices. We can then re-define it as a simply-connected region bounded by p distinct segments. (“ Simply-connected ” means that every simple closed curve drawn in the region can be shrunk to a point without leaving the region, i.e., that there are no holes.)

The most important case is when none of the bounding lines (or “ sides produced ”) penetrate the region. We then have a convex p-gon, which may be described (in terms of Cartesian coordinates) by a system of p linear inequalities

These inequalities must be consistent but not redundant, and must provide the range for a finite integral

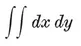
(which measures the area).

A polygon is said to be equilateral if its sides are all equal, equiangular if its angles are all equal. If p > 3, a p-gon can be equilateral without being equiangular, or vice versa ; e.g., a rhomb is equilateral, and a rectangle is equiangular. A plane p-gon is said to be regular if it is both equilateral and equiangular. It is then denoted by {p} ; thus {3} is an equilateral triangle, {4} is a square, {5} is a regular pentagon, and so on.

A regular polygon is easily seen to have a centre, from which all the vertices are at the same distance ₀R, while all the sides are at the same distance ₁R. This means that there are two concentric circles, the circum-circle and in-circle, which pass through the vertices and touch the sides, respectively.

It is sometimes helpful to think of the sides of a p-gon as representing p vectors whose sum is zero. They may then be compared with p segments issuing from one point, the angle between two consecutive segments being equal to an exterior angle of the p-gon. It follows that the sum of the exterior angles of a plane polygon is a complete turn, or 2π. Hence each exterior angle of {p} is 2π/p, and the interior angle is the supplement,

1·11

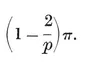
This may alternatively be seen from the right-angled triangle O₂ O₁ O₀ of Fig. 1.1A, where O₂ is the centre, O₁ is the mid-point of a side, and O₀ is one end of that side. The right angle occurs at O₁, and the angle at O₂ is evidently π/p. If 2l is the length of the side, we have

O₀ O₁ = l, O₀ O₂ = ₀R, O₁ O₂ = ₁R ;

therefore

1·12

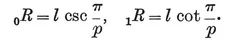
The area of {p}, being made up of 2p such triangles, is

1·13

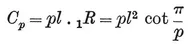
(in terms of the half-side l). The perimeter is, of course,

1·14

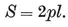
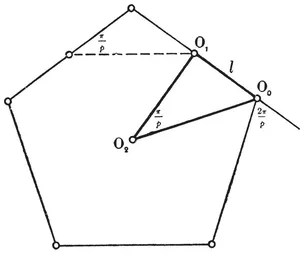
FIG. 1.1A

As p increases without limit, the ratios S/₀R and S/₁R both tend to 2π, as we would expect. (This is how Archimedes estimated π, taking p=96.)

We may take the Cartesian coordinates of the vertices to be

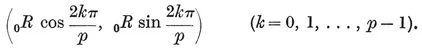
Then, in the Argand diagram, the vertices of a {p} of circum-radius ₀R=1 represent the complex numbers e^2kπi/p, which are the roots of the cyclotomic equation

1·15

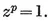
It is sometimes desirable to extend our ...