
eBook - ePub
Feedback Control Theory
- 224 pages
- English
- ePUB (mobile friendly)
- Available on iOS & Android
eBook - ePub
Feedback Control Theory
About this book
An excellent introduction to feedback control system design, this book offers a theoretical approach that captures the essential issues and can be applied to a wide range of practical problems. Its explorations of recent developments in the field emphasize the relationship of new procedures to classical control theory, with a focus on single input and output systems that keeps concepts accessible to students with limited backgrounds. The text is geared toward a single-semester senior course or a graduate-level class for students of electrical engineering.
The opening chapters constitute a basic treatment of feedback design. Topics include a detailed formulation of the control design program, the fundamental issue of performance/stability robustness tradeoff, and the graphical design technique of loopshaping. Subsequent chapters extend the discussion of the loopshaping technique and connect it with notions of optimality. Concluding chapters examine controller design via optimization, offering a mathematical approach that is useful for multivariable systems.
The opening chapters constitute a basic treatment of feedback design. Topics include a detailed formulation of the control design program, the fundamental issue of performance/stability robustness tradeoff, and the graphical design technique of loopshaping. Subsequent chapters extend the discussion of the loopshaping technique and connect it with notions of optimality. Concluding chapters examine controller design via optimization, offering a mathematical approach that is useful for multivariable systems.
Tools to learn more effectively

Saving Books

Keyword Search

Annotating Text

Listen to it instead
Information
Chapter 1
Introduction
Without control systems there could be no manufacturing, no vehicles, no computers, no regulated environment—in short, no technology. Control systems are what make machines, in the broadest sense of the term, function as intended. Control systems are most often based on the principle of feedback, whereby the signal to be controlled is compared to a desired reference signal and the discrepancy used to compute corrective control action. The goal of this book is to present a theory of feedback control system design that captures the essential issues, can be applied to a wide range of practical problems, and is as simple as possible.
1.1 Issues in Control System Design
The process of designing a control system generally involves many steps. A typical scenario is as follows:
1.Study the system to be controlled and decide what types of sensors and actuators will be used and where they will be placed.
2.Model the resulting system to be controlled.
3.Simplify the model if necessary so that it is tractable.
4.Analyze the resulting model; determine its properties.
5.Decide on performance specifications.
6.Decide on the type of controller to be used.
7.Design a controller to meet the specs, if possible; if not, modify the specs or generalize the type of controller sought.
8.Simulate the resulting controlled system, either on a computer or in a pilot plant.
9.Repeat from step 1 if necessary.
10.Choose hardware and software and implement the controller.
11.Tune the controller on-line if necessary.
It must be kept in mind that a control engineer's role is not merely one of designing control systems for fixed plants, of simply “wrapping a little feedback” around an already fixed physical system. It also involves assisting in the choice and configuration of hardware by taking a systemwide view of performance. For this reason it is important that a theory of feedback not only lead to good designs when these are possible, but also indicate directly and unambiguously when the performance objectives cannot be met.
It is also important to realize at the outset that practical problems have uncertain, non- minimum-phase plants (non-minimum-phase means the existence of right half-plane zeros, so the inverse is unstable); that there are inevitably unmodeled dynamics that produce substantial uncertainty, usually at high frequency; and that sensor noise and input signal level constraints limit the achievable benefits of feedback. A theory that excludes some of these practical issues can still be useful in limited application domains. For example, many process control problems are so dominated by plant uncertainty and right half-plane zeros that sensor noise and input signal level constraints can be neglected. Some spacecraft problems, on the other hand, are so dominated by tradeoffs between sensor noise, disturbance rejection, and input signal level (e.g., fuel consumption) that plant uncertainty and non-minimum-phase effects are negligible. Nevertheless, any general theory should be able to treat all these issues explicitly and give quantitative and qualitative results about their impact on system performance.
In the present section we look at two issues involved in the design process: deciding on performance specifications and modeling. We begin with an example to illustrate these two issues.
Example A very interesting engineering system is the Keck astronomical telescope, currently under construction on Mauna Kea in Hawaii. When completed it will be the world’s largest. The basic objective of the telescope is to collect and focus starlight using a large concave mirror. The shape of the mirror determines the quality of the observed image. The larger the mirror, the more light that can be collected, and hence the dimmer the star that can be observed. The diameter of the mirror on the Keck telescope will be 10 m. To make such a large, high-precision mirror out of a single piece of glass would be very difficult and costly. Instead, the mirror on the Keck telescope will be a mosaic of 36 hexagonal small mirrors. These 36 segments must then be aligned so that the composite mirror has the desired shape.
The control system to do this is illustrated in Figure 1.1. As shown, the mirror segments are subject to two types of forces: disturbance forces (described below) and forces from actuators. Behind each segment are three piston-type actuators, applying forces at three points on the segment to effect its orientation. In controlling the mirror’s shape, it suffices to control the misalignment between adjacent mirror segments. In the gap between every two adjacent segments are (capacitor-type) sensors measuring local displacements between the two segments. These local displacements are stacked into the vector labeled y; this is what is to be controlled. For the mirror to have the ideal shape, these displacements should have certain ideal values that can be pre-computed; these are the components of the vector r. The controller must be designed so that in the closed-loop system y is held close to r despite the disturbance forces. Notice that the signals are vector valued. Such a system is multivariable.
Our uncertainty about the plant arises from disturbance sources:
•As the telescope turns to track a star, the direction of the force of gravity on the mirror changes.
•During the night, when astronomical observations are made, the ambient temperature changes.
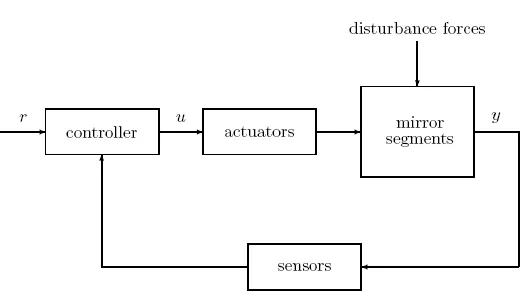
Figure 1.1: Block diagram of Keck telescope control system.
•The telescope is susceptible to wind gusts.
and from uncertain plant dynamics:
•The dynamic behavior of the components—mirror segments, actuators, sensors—cannot be modeled with infinite precision.
Now we continue with a discussion of the issues in general.
Control Objectives
Generally speaking, the objective in a control system is to make some output, say y, behave in a desired way by manipulating some input, say u. The simplest objective might be to keep y small (or close to some equilibrium point)—a regulator problem—or to keep y − r small for r, a reference or command signal, in some set—a servomechanism or servo problem. Examples:
•On a commercial airplane the vertical acceleration should be less than a certain value for passenger comfort.
•In an audio amplifier the power of noise signals at the output must be sufficiently small for high fidelity.
•In papermaking the moisture content must be kept between prescribed values.
There might be the side constraint of keeping u itself small as well, because it might be con...
Table of contents
- Cover
- Title Page
- Contents
- Preface
- 1 Introduction
- 2 Norms for Signals and Systems
- 3 Basic Concepts
- 4 Uncertainty and Robustness
- 5 Stabilization
- 6 Design Constraints
- 7 Loopshaping
- 8 Advanced Loopshaping
- 9 Model Matching
- 10 Design for Performance
- 11 Stability Margin Optimization
- 12 Design for Robust Performance
- References
- Index
Frequently asked questions
Yes, you can cancel anytime from the Subscription tab in your account settings on the Perlego website. Your subscription will stay active until the end of your current billing period. Learn how to cancel your subscription
No, books cannot be downloaded as external files, such as PDFs, for use outside of Perlego. However, you can download books within the Perlego app for offline reading on mobile or tablet. Learn how to download books offline
Perlego offers two plans: Essential and Complete
- Essential is ideal for learners and professionals who enjoy exploring a wide range of subjects. Access the Essential Library with 800,000+ trusted titles and best-sellers across business, personal growth, and the humanities. Includes unlimited reading time and Standard Read Aloud voice.
- Complete: Perfect for advanced learners and researchers needing full, unrestricted access. Unlock 1.4M+ books across hundreds of subjects, including academic and specialized titles. The Complete Plan also includes advanced features like Premium Read Aloud and Research Assistant.
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 990+ topics, we’ve got you covered! Learn about our mission
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more about Read Aloud
Yes! You can use the Perlego app on both iOS and Android devices to read anytime, anywhere — even offline. Perfect for commutes or when you’re on the go.
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app
Please note we cannot support devices running on iOS 13 and Android 7 or earlier. Learn more about using the app
Yes, you can access Feedback Control Theory by John C. Doyle,Bruce A. Francis,Allen R. Tannenbaum, Bruce A. Francis, Allen R. Tannenbaum in PDF and/or ePUB format, as well as other popular books in Technology & Engineering & Electrical Engineering & Telecommunications. We have over one million books available in our catalogue for you to explore.