Mechanical Vibration Analysis and Computation

D. E. Newland

• Publisher: Dover Publications
• Year: 2013
• eBook ISBN: 9780486317724
• Topic: Physical Sciences
• Subtopic: Mechanics

Focusing on applications rather than rigorous proofs, this volume is suitable for upper-level undergraduates and graduate students concerned with vibration problems. In addition, it serves as a practical handbook for performing vibration calculations.
An introductory chapter on fundamental concepts is succeeded by explorations of frequency response of linear systems and general response properties, matrix analysis, natural frequencies and mode shapes, singular and defective matrices, and numerical methods for modal analysis. Additional topics include response functions and their applications, discrete response calculations, systems with symmetric matrices, continuous systems, and parametric and nonlinear effects. The text is supplemented by extensive appendices and answers to selected problems.
This volume functions as a companion to the author's introductory volume on random vibrations (see below). Each text can be read separately; and together, they cover the entire field of mechanical vibrations analysis, including random and nonlinear vibrations and digital data analysis.

Chapter 1

Fundamental concepts

General solution for one degree of freedom

The vibration behaviour of many real systems can be approximated by a physical model with one degree of freedom defined by

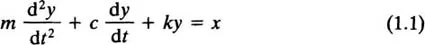
where x ≡ x(t) is the excitation and y ≡ y(t) is the response, which are both functions of time, t. The constants m, c and k represent the mass, viscous damping and stiffness of the system, which is shown in Fig. 1.1. If there is no excitation, so that x(t) = 0, this has the general solution

where C₁ and C₂ are arbitrary constants determined by the initial conditions and the eigenvalues λ₁, λ₂ are the two roots of the characteristic equation

which we assume are distinct so that λ₁ ≠ λ₂. When x(t) is not zero, the solution from y(t) can be written in the form

Fig. 1.1 Single-degree-of-freedom system with force input x(t) and displacement output y(t)

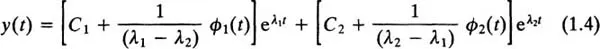
where ϕ₁(t) and ϕ₂(t) are the indefinite integrals

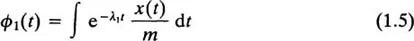
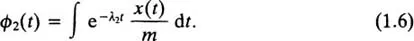
Each integral introduces an arbitrary constant of integration; in (1.4) these are given by the constants C₁ and C₂, which must be chosen to satisfy the initial conditions.

In Chapter 4 we shall derive the solution (1.4) from first principles, but the reader can check that the answer given is correct by differentiating (1.4) to obtain ẏ and ÿ and then substituting these expressions into the left-hand side of (1.1). The result for ẏ is

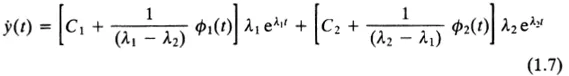
as may be verified from Problem 1.1. On first inspection it appears that (1.7) cannot be the result of differentiating (1.4) because the functions ϕ₁(t) and ϕ₂(t) do not appear to have been differentiated. However, because of the form of (1.5) and (1.6),

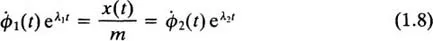
and so these terms cancel out in (1.7).

If, at time t = 0, the initial conditions are y(0) and ẏ(0), and the integrals in (1.5) and (1.6) have the values ϕ₁(0) and ϕ₂(0), then, from (1.4),

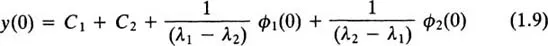
and, from (1.7),

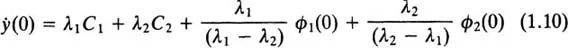
from which

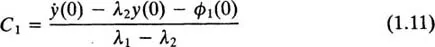
and

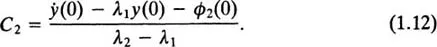
On substituting in (1.4) for C₁ and C₂ from (1.11) and (1.12), we find that the general solution for y(t) can be writt...

Table of contents

• Cover
• Title Page
• Copyright Page
• Contents
• Preface
• Disclaimer of warranty
• Selected topics for a first course on vibration analysis and computation
• Acknowledgements
• Chapter 1: Fundamental concepts
• Chapter 2: Frequency response of linear systems
• Chapter 3: General response properties
• Chapter 4: Matrix analysis
• Chapter 5: Natural frequencies and mode shapes
• Chapter 6: Singular and defective matrices
• Chapter 7: Numerical methods for modal analysis
• Chapter 8: Response functions
• Chapter 9: Application of response functions
• Chapter 10: Discrete response calculations
• Chapter 11: Systems with symmetric matrices
• Chapter 12: Continuous systems I
• Chapter 13: Continuous systems II
• Chapter 14: Parametric and nonlinear effects
• Appendices: Logical flow diagrams
• Problems
• Answers to selected problems
• List of references
• Summary of main formulae
• Index