Computational Physics

Fortran Version

Steven E. Koonin

• Publisher: CRC Press
• Year: 2018
• ISBN:
  9780429973659
• Edition: 1
• Topic: Ciencias físicas
• Subtopic: Física

Computational Physics is designed to provide direct experience in the computer modeling of physical systems. Its scope includes the essential numerical techniques needed to "do physics" on a computer. Each of these is developed heuristically in the text, with the aid of simple mathematical illustrations. However, the real value of the book is in the eight Examples and Projects, where the reader is guided in applying these techniques to substantial problems in classical, quantum, or statistical mechanics. These problems have been chosen to enrich the standard physics curriculum at the advanced undergraduate or beginning graduate level. The book will also be useful to physicists, engineers, and chemists interested in computer modeling and numerical techniques. Although the user-friendly and fully documented programs are written in FORTRAN, a casual familiarity with any other high-level language, such as BASIC, PASCAL, or C, is sufficient. The codes in BASIC and FORTRAN are available on the web at http://www.computationalphysics.info. They are available in zip format, which can be expanded on UNIX, Window, and Mac systems with the proper software. The codes are suitable for use (with minor changes) on any machine with a FORTRAN-77 compatible compiler or BASIC compiler. The FORTRAN graphics codes are available as well. However, as they were originally written to run on the VAX, major modifications must be made to make them run on other machines.

Chapter 1

Basic Mathematical Operations

Three numerical operations — differentiation, quadrature, and the finding of roots — are central to most computer modeling of physical systems. Suppose that we have the ability to calculate the value of a function, f(x), at any value of the independent variable x. In differentiation, we seek one of the derivatives of f at a given value of x. Quadrature, roughly the inverse of differentiation, requires us to calculate the definite integral of f between two specified limits (we reserve the term “integration” for the process of solving ordinary differential equations, as discussed in Chapter 2), while in root finding we seek the values of x (there may be several) at which f vanishes.

If f is known analytically, it is almost always possible, with enough fortitude, to derive explicit formulas for the derivatives of f, and it is often possible to do so for its definite integral as well. However, it is often the case that an analytical method cannot be used, even though we can evaluate f(x) itself. This might be either because some very complicated numerical procedure is required to evaluate f and we have no suitable analytical formula upon which to apply the rules of differentiation and quadrature, or, even worse, because the way we can generate f provides us with its values at only a set of discrete abscissae. In these situations, we must employ approximate formulas expressing the derivatives and integral in terms of the values of f we can compute. Moreover, the roots of all but the simplest functions cannot be found analytically, and numerical methods are therefore essential.

This chapter deals with the computer realization of these three basic operations. The central technique is to approximate f by a simple function (such as first- or second-degree polynomial) upon which these operations can be performed easily. We will derive only the simplest and most commonly used formulas; fuller treatments can be found in many textbooks on numerical analysis.

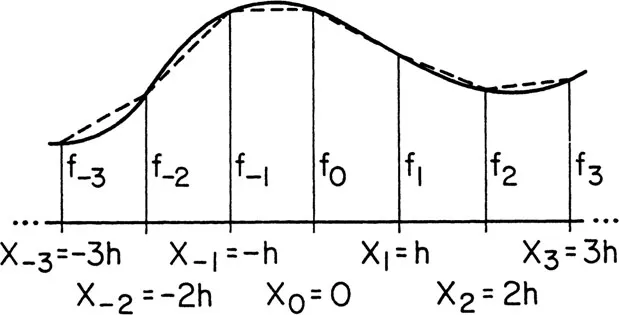
Figure 1.1 Values of f on an equally-spaced lattice. Dashed lines show the linear interpolation.

1.1 Numerical differentiation

Let us suppose that we are interested in the derivative at x = 0, f′(0). (The formulas we will derive can be generalized simply to arbitrary x by translation.) Let us also suppose that we know f on an equally-spaced lattice of x values,

$\begin{array}{cc}{f}_n=f(x_n);& x_n=nh(n=0,\pm 1,\pm 2,\dots )\end{array},$

and that our goal is to compute an approximate value of f′(0) in terms of the f_n (see Figure 1.1).

We begin by using a Taylor series to expand f in the neighborhood of x = 0:

$f(x)=f_0+x{f}^{\prime }+\frac{x^2}{2!}{f}^{″}+\frac{x^3}{3!}{f}^{‴}+\dots ,$

(1.1)

where all derivatives are evaluated at x = 0. It is then simp...

Table of contents

• Cover
• Half Title
• Title Page
• Copyright Page
• Table of Contents
• Preface
• Preface to the FORTRAN Edition
• How to use this book
• Chapter 1: Basic Mathematical Operations
• Chapter 2: Ordinary Differential Equations
• Chapter 3: Boundary Value and Eigenvalue Problems
• Chapter 4: Special Functions and Gaussian Quadrature
• Chapter 5: Matrix Operations
• Chapter 6: Elliptic Partial Differential Equations
• Chapter 7: Parabolic Partial Differential Equations
• Chapter 8: Monte Carlo Methods
• Appendix A: How to use the programs
• Appendix B: Programs for the Examples
• Appendix C: Programs for the Projects
• Appendix D: Common Utility Codes
• Appendix E: Network File Transfer
• References
• Index