Introducing Difficult Mathematics Topics in the Elementary Classroom

A Teacher’s Guide to Initial Lessons

Francis J. Gardella

• Publisher: Routledge
• Year: 2008
• Print ISBN: 9781138460249
• eBook ISBN: 9781135890902
• Topic: Education
• Subtopic: Education General

This exciting text for the pre-service elementary teacher provides hands on mathematics lessons they can use to introduce mathematical concepts and skills that students find particularly challenging. Each chapter is divided into four sections:

The Activity employs an engaging thought experiment to help the reader "visit a classroom" to understand how the lesson used to introduce the concept or skill would materialize in the class.

The Mathematics provides the necessary mathematical background used in the lesson to make the actual teaching/learning situation comfortable for both the teachers and the learner.

The Plan provides the reader with an actual lesson plan to engage the Activity in the classroom setting.

Putting It All Together pulls the previous sections together with a summary of the chapter as well as further information for making the lesson successful.

By providing models of what excellent lessons on a given topic look like, knowledge of the mathematics involved, and a concrete lesson plan structure this much-needed resource is the definitive mathematics planning vehicle that every teacher will want before they set foot in their own elementary classroom.

1
HOW CHILDREN LEARN MATHEMATICS (AND WHY IT DOESN’T HAPPEN!)

Mathematics and Language

The acquisition of the ability to communicate using oral language is a natural phenomenon of the human species. We learn to speak. This acquisition of oral language and the way we learn to link the oral to the symbolic language expressions of reading and writing suggest to me a model for the way children learn and understand the language of mathematics.

The place of language in the learning of mathematics has been discussed for some time. In fact, according to A. G. Howson (1983), it was stated by John Dee as early as the 16th century that books in English would make for

“better and easier learning and would help students proceed more cheerfully, more skillfully and speedily forward” (Dee, 1570). Yet Dee’s thesis that mathematics cannot truly enter a nation’s life until it enters the nation’s language is, I feel certain, a valid one.

This is pretty heady stuff. Actually, Dee was advocating the use of English language texts in the study of mathematics as opposed to the then prevalent use of texts written in Latin and Greek. (I know many people who today still think that mathematics is mostly Latin and Greek and not because of pi.)

I would like you to consider the validity of the idea of using under-standable language in a student’s initial learning and further development of mathematics. In one way, it has to do with what Vygotsky called private speech, when children “talk to themselves as they go about their daily activities. This self-talk or overt speech…does not seem to be addressed to another person…” (cited in Berk & Winsler, p. 34). In a way, this is the type of communication which all initial learners use, including ourselves, when we learn something new; that is, we use known language in approaching unknown ideas and concepts.

So, as we move on, I would like you to consider teaching mathematics from the point of view of using known language and vocabulary to have students understand mathematical content and then addressing the more formal vocabulary and symbolic formats of mathematical communication. I call this the linguistic/mathematical learning model. (Notice that I told you what it was about before I named it!!!)

Children learn to use linguistic/language structures in stages as they develop proficiency with language from oral to symbolic (reading and writing). There are a set of similar stages by which a learner should develop a knowledge of mathematics and its associated language structure and vocabulary (from the conceptual to the symbolic and formal).

Learning Mathematics—The Present

In the development of vocabulary in terms of literacy, there is a time frame which begins with introducing children to a new idea and then gradually requires formal use of the word in both oral and written form. Because in many people’s minds the study of mathematical ideas is irrevocably linked to the vocabulary used, as if without the formal vocabulary we could not think about mathematical ideas, this time frame is not a part of the learning sequence in mathematics. It happens almost immediately. When a new concept or skill is introduced we see very little time for the use of any communication device at any level other than the formal written/symbolic. If a mathematical concept or skill is to be addressed at a certain grade level, its introduction, development, and use as part of a formal symbolic system all appear in that grade level and in some cases, in the same chapter or chapter subsections.

In the teaching of mathematics, there seems to be a rush to expect children to automatically develop an understanding of a concept after its initial introduction while at the same time expecting students to use the ideas in their most abstract and symbolic forms.

As a counter to this, the teaching/learning structure you will see in all chapters of this book involves having the students first understand the nature of the mathematics and then move on to the symbolic and formal issues. In chapter 2, the lesson is about finding the median of a set of data. You will see how the lesson is first to have students find the middle number and then use it to analyze data. The introduction of vocabulary, such as median or outliers for the smallest and largest values needs to be accomplished but should be integrated into the end of the second, maybe even the third lesson. The theme in this first lesson and all the other lessons is to give the students one new idea at a time, namely the concept, and having them discuss it using their social language structure before they begin to address the formal symbolic level of the mathematics with its accompanying vocabulary.

Unfortunately, in many mathematics curricula and texts, there is no place for earlier work on a topic at a nonsymbolic/technical level to set the stage for later work on a symbolic level. When some concepts are addressed at a prior grade, it is either done as a one-page insert in the text or at the end of the text in basically a formal symbolic manner.

As an example, look at the previewing of multiplication at the end of Grade 2 as readiness for study in Grade 3. If multiplication is addressed at the end of the program in Grade 2, the content moves quickly from a pictorial representation to the symbolic display of the multiplication facts with the use of× sign as the operator. Although some counting by 2 or 5 or 10 (skip counting) is done during this year as well as in Grade 1 as part of lessons on number patterns, many times it is not related to multiplication addressed here or in Grade 3.

However, let us be clear. It is extremely important that students not just learn but acquire functional use of the formal symbolic representation of mathematics. Students need to know how to communicate mathematics utilizing the system which is well accepted throughout the world. The issue here is not to water down the use of formal symbolic representations, but to call for their learning and use in a proper timeframe, allowing children to understand the concepts and skills involved prior to the development of symbolic representation. And, there are enough years of school to address the symbolic/technical representations in a proper manner.

The model for the lessons in this book places the learning of mathematics and the learning of the related symbolism into proper perspective. As noted previously, the model views the learning of mathematics as a parallel to language development. This demands a period of nonsymbolic development and understanding before the formal written communication conventions of mathematical symbolism are addressed. As in the lesson about division (chapter 5), students must see the process used in problem solving situations before being required to use it to communicate in the conventional symbolic manner. This model as it is demonstrated in all the teaching lessons in this book shows how the mathematics can be addressed without the initial use of the technical vocabulary and symbolic representations. The lessons in this book are for initial teaching, the most difficult part of the teaching process.

Learning Mathematics: A Continuum

The view that the learning of mathematics is similar to the learning of a new or second language suggests that language learning development forms the basis for the model in the learning of mathematics that is used with the lessons in the following chapters.

Learning takes place in many ways. One of the basic ideas supported by cognitive psychologists such as Piaget and Bruner (cited in Pulaski, 1971, pp. 13–28) is that a person learns along a continuum. Piaget elaborated this theory on four stages: Sensorimotor, Preop-erational, Concrete Operational, and Formal Operations and Bruner on three: Enactive (action), Ikonic (imagery), and Symbolic (language). The model for the lessons in this book is adapted from these theories.

During a concrete phase, children begin with the use of physical objects such as Cuisenaire rods, Dienes blocks (base-ten materials), pattern blocks, and then diagrams and pictures to develop and discuss ideas informally, while rising through initial levels of abstraction all moving the student toward the symbolic formats we as adults know. In this model, abstraction is not seen as a singular level unto itself but as a maturing cognitive process of the learner where the learner moves from an initial phase of abstraction brought on by the interaction with physical models into more complex levels of thinking with symbolism being used as the representation.

It is in a connecting stage that learners begin to relate the physical/pictorial representations of their ideas to conventional symbolism used to communicate mathematics. Moving through levels of abstraction the learners come to a symbolic stage where they can now represent mathematics using the conventional written symbolism and vocabulary. In the connecting stage, learners see the relationship of the modeling they have done in the concrete stage to the symbolic representations by which people communicate mathematically. Figure 1.1, the mathematics learning model, shows the relationship between these stages and the continuum of abstraction involved in the learning of mathematics.

The development of abstraction along a continuum is somewhat different from ideas fostered in the thinking of how one learns mathematics. People mostly think of abstraction in mathematics as being the final stage of learning. But suppose a student can do part of the work with physical models and another part of the work without them. Then this student level of abstraction is higher and more cognitively mature than a student who needs the physicality for the entire problem; however, it is not as mature as a student who can accomplish the task with no need of physical models. For example, suppose students are given a problem in which 42 items are shared between two people. Initial teaching will take place using physical models. However, after this, some students will not need to actually have the base-ten blocks (4 tens and 2 ones) in front of them to find that the answer does not require a trade of 1 ten block for 10 ones.

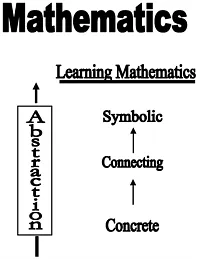
Figure 1.1

Yet, this same student may need to have materials available if the problem calls for the sharing of 42 apples with three people in order to see that a trade of 1 ten for 10 ones is called for (see chapter 5 for further elaboration on sharing as an introductory model for division). At this level of abstraction, the student would actually take the blocks and use them to establish the need for the trade. Another student whose level of abstraction is even more mature may make the decision about trading before even setting up such physical models, although this student may still need the models to obtain an answer. This last type of advanced decision making certainly is not the highest abstract level of thinking but will occur before any written symbolism is used.

In summary, the level of abstraction used in recognizing the need for a trade before distributing the blocks is certainly more developed than that utilized in the first instance where the child needs to work with the blocks before deciding a trade is necessary. The lessons in this book follow such an idea that abstraction occurs along a developmental continuum initiated from the very beginning of learning. As learners move from the connecting to symbolic stages (see Figure 1.1), they develop the use and control of symbolism in communicating mathematics.

Communicating Mathematics: A Language Continuum

The focus here is how the movement through the stages of learning mathematics impacts on the student’s acquisition of mathematical terminology and symbolism. As a student begins the learning sequence at the concrete stage, the initial manner of communication is the oral/ social level language of the learner, a language of understanding that the student brings into the classroom. It is this language which allows the student to develop realizations and understandings of the mathematics. In the concrete stage, developing mathematical understanding is accomplished without the interference of symbolic structures and technical vocabulary which is as new to the learner as the mathematical concepts involved.

As the learner moves through the connecting stage toward symbolic representation, there is a place then for relating this language of understanding to the development of the language of formalism which is comprised of the symbolism and technical vocabulary which are considered mathematically appropriate. Figure 1.2, where the mathematics learning model becomes the model of mathematics learning/ language development, shows this in relation to the stages of learning mathematics as well as the movement along the abstraction continuum.

As stated previously, for many people, the relationship of mathematics to its symbols and vocabulary is one and same. This idea makes it seem that without technical vocabulary and symbols, there is no mathematics. But, one must remember that the symbolism and vocabulary of mathematics, as with any written linguistic system, are arbitrary not natural; they are developed by people to enable communication to take place. Therefore these systems need a learning experience after what they represent is internalized.

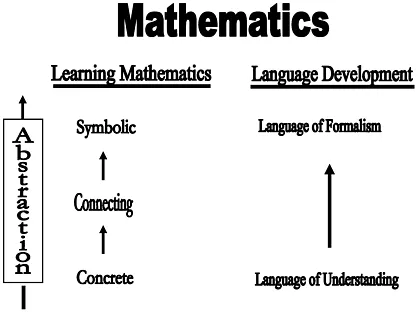
Figure 1.2

The model here at the outset of the learning process develops ideas first and then vocabulary/symbolism. For, at the concrete stage, while developing from a language of understanding, there is little if any formalized mathematical writing in the traditional mathematical sense. Writing done here is in the student’s own language, and it is used to explain what is occurring and to communicate a solution to a problem.

As the student moves into the connecting stage, written mathematical symbolism is introduced. But it is done in a way that allows students to substitute a sophisticated, arbitrary symbolic communication system (any formal oral/written language is an arbitrary symbolic system) for one that they already know, their language of understanding and physical representations. The focus then is to enable students to link the ideas which they already understand to the written symbols that are used by the mathematical community to communicate mathematical ideas. It is on this oral to written language continuum that students learn to represent mathematics symbolically and to use the content-related vocabulary for communication.

An example of the mathematics/language learning model in the learning of fractions in the early grades illustrates this. As will be discussed in greater detail in chapter 6, although children in the early grades do understand ideas such as half, the symbol ½ may be seen as two whole numbers (1 and 2) as opposed to one symbol representing a half—as a learner with more developed ability to think in abstract terms, say in Grade 4, may see it. In this case, this representation and interpretation may in fact be setting the stage for later misinterpretation especially in addition, such as 2/3+½ where the incorrect answer 3/5 is often seen. In other words, the concurrent teaching of concept and symbolism may be counterproductive to the learning of fractions. It is the case for many of the students that I have trained to be elementary mathematics teachers.

In Figure 1.3, the previously mentioned continuum of oral to written language is placed in the model. Note that the idea of written language is positioned below that of the language of formalism. This is because students’ writing does not begin at the symbolic stage but begins with the use of the language of understanding and develops until the students’ knowledge ...

Table of contents

• COVER PAGE
• TITLE PAGE
• COPYRIGHT PAGE
• INTRODUCTION
• 1 HOW CHILDREN LEARN MATHEMATICS (AND WHY IT DOESN’T HAPPEN!)
• 2 MEDIAN: FINDING WHAT’S IN THE MIDDLE
• 3 ROUNDING: THE MYSTERY OF “ROUNDING UP FOR 5”
• 4 SKIPPING MULTIPLICATION (OR AT LEAST THROUGH IT)
• 5 LEARNING TO USE DIVISION
• 6 FRACTIONS: WHAT’S IT ALL ABOUT?
• 7 FRACTIONS: ADDING UNLIKE THINGS? IMPOSSIBLE!
• 8 FRACTIONS: DIVIDING INTO SMALL PIECES?
• 9 DECIMALS: OPERATIONS BEFORE RULES
• 10 MEASUREMENT: MAKE YOUR OWN RULER
• 11 AREA: SKIPPING THROUGH THE ROWS
• 12 VOLUME: IT’S LIKE LOOKING AT AN APARTMENT HOUSE…
• 13 MEAN: HOW MUCH DOES EACH GET?
• 14 PERCENT: LEVELING THE FIELD OF COMPARISON
• 15 ORDER OF OPERATIONS: AN AGREEMENT? DID YOU GET THE MEMO?
• APPENDIX A
• APPENDIX B
• BIBLIOGRAPHY